Differenzierbare Mannigfaltigkeit
Inhalt
4.1. Differenzierbare Mannigfaltigkeit¶
4.1.1. Topologische Räume¶
Wir haben bisher immer Mathematik auf metrischen oder gar normierten Vektorräumen betrieben, da uns diese Struktur für alle erklärten Konzepte am dienlichsten war (siehe Kapitel 4 & 5 in [Bur20] und MP-2 Skript). Als Vorbereitung für Mannigfaltigkeiten wollen wir von den metrischen Räumen zu allgemeineren Strukturen wechseln - den sogenannten topologischen Räumen.
Das zentrale Konzept topologischer Räume ist die folgende Definition der offene Mengen.
Definition 4.1 (Offene Mengen und topologischer Raum)
Sei \(\M\) eine Menge und \(\tau \subset 2^\M\) eine Teilmenge der Potenzmenge. Wir nennen das Tupel \((\M,\tau)\) topologischer Raum, falls die folgenden Eigenschaften erfüllt sind,
\(\emptyset, \M \in \tau\),
für eine beliebige (insbesondere auch unendlich große) Indexmenge \(\mathcal{I}\) seien \(U_i\in\tau, i\in \mathcal{I}\). Dann gilt auch schon \(\bigcup_{i\in I} U_i \in \tau\),
für endlich viele \(U_j\in\tau, j=1,\ldots, k\) gilt auch schon \(\bigcap_{j=1}^k U_j \in \tau\).
Wir bezeichnen mit \(\tau\) die Topologie des Raumes und dessen Elemente \(U\in\tau\) heißen offene Mengen. Für jeden Punkt \(x\in \M\) nennen wir eine offene Menge \(U(x) \in \tau\) Nachbarschaft oder Umgebung um \(x\), falls \(x\in U(x)\).
Analog zur Definition auf metrischen Räumen bezeichnen wir das Komplement \(\M \setminus U\) \einer offenen Menge \(U\) als abgeschlossen.
Es gibt viele interessante topologische Räume, die den Namen ihrer Entdecker tragen, wie zum Beispiel der Arens-Fort-Raum, der Cantor-Raum, oder der Hilbertwürfel. Im Folgenden wollen wir ein relativ generisches Beispiel für einen topologischen Raum betrachten.
Example 4.1 (Diskrete Topologie)
Es sei \(M\) eine beliebige Menge. Dann können wir eine Topologie \(\tau\) auf \(\M\) definieren, in dem wir alle Teilmengen von \(\M\) als offen definieren. In diesem Beispiel folgt trivialerweise, dass \(\tau = \mathcal{P}(\M)\) gilt. Dann ist \((\M, \tau)\) ein topologischer Raum. Diese Topologie nennt man diskrete Topologie, da für jeden diskreten Punkt \(x \in \M\) die Menge \(\lbrace x \rbrace\) offen ist.
Die diskrete Topologie wird durch eine spezielle Metrik erzeugt, wie man im Folgenden einsieht. Seien \(x,y \in M\) Punkte der Menge und \(d \colon \M \times \M \rightarrow \R^+_0\) eine Metrik auf \(\M\) mit
Über diese Metrik kann man nun offene Umgebungen von Punkten \(x \in \M\) wie folgt konstruieren,
Dies führt dazu, dass alle Teilmengen, die nur einen Punkt der Menge enthalten, offen sind. Über beliebige Vereinigung dieser Punktmengen, lassen sich dann alle Teilmengen der Potenzmenge \(\mathcal{P}(\M)\) als offen definieren und man erhält somit die diskrete Topologie.
Remark 4.1 (Notation von topologischen Räumen)
Häufig spielt die konkrete Wahl einer Topologie \(\tau \subset \mathcal{P}(\M)\) keine Rolle für die mathematischen Aussagen, die man treffen möchte. Da wir jede beliebige Menge \(\M\) mit der diskreten Topologie aus Example 4.1 zu einem topologischen Raum \((\M, \tau)\) ausstatten können, wird die Angabe der konkreten Topologie \(\tau\) häufig ausgelassen. In solchen Fällen identifiziert man den topologischen Raum einfach mit der zu Grunde liegenden Menge \(\M\), d.h., wir nennen \(\M\) einen topologischen Raum, wenn die konkrete Topologie im gewählten Kontext eindeutig ist oder keine Rolle spielt.
Viele mathematische Konzepte lassen sich von metrischen oder normierten Räumen auf topologische Räume übertragen, wie zum Beispiel der Begriff einer stetigen Funktion.
Definition 4.2 (Stetige Funktionen auf topologischen Räumen)
Seien \((\M_1, \tau_1)\) und \((\M_2, \tau_2)\) topologische Räume und \(f\) eine Funktion mit
Wir nennen \(f\) stetig, wenn die Urbilder offener Mengen in \(\tau_2\) unter \(f\) wieder offene Mengen in \(\tau_1\) ergeben, d.h.,
Das folgende Diagramm zeigt die Relationen zwischen verschiedenen mathematischen Konzepten innerhalb einer hierarchischen Struktur.
4.1.2. Mannigfaltigkeiten¶
In diesem Abschnitt führen wir das grundlegende Konzept von Mannigfaltigkeiten als Spezialfall eines topologischen Raums ein, der lokal mit dem Euklidischen Raum \(\R^n\) identifiziert werden kann. Mannigfaltigkeiten spielen insbesondere im mathematischen Teilgebiet der Differentialgeometrie eine zentrale Rolle.
4.1.2.1. Motivation¶
Das wohl verständlichste Bild einer Mannigfaltigkeit ist die Oberfläche einer dreidimensionalen Kugel
wie sie zum Beispiel genutzt wird um die Erdoberfläche zu modellieren. Möchte man Mathematik auf solch einer Oberfläche betreiben, so benötigt man vollkommen andere Konzepte als in offenen Teilmengen des \(\R^n\). Möchte man beispielsweise berechnen, wie weit man reisen muss, um von einem Punkt auf der Oberfläche zu einem anderen Punkt zu kommen, so benötigt man einen angepassten Abstandsbegriff, da die Euklidische Norm nur die direkte Entfernung messen würde, welche die Kugeloberfläche jedoch durchschneidet. Dies ist in folgender Abbildung visualisiert.
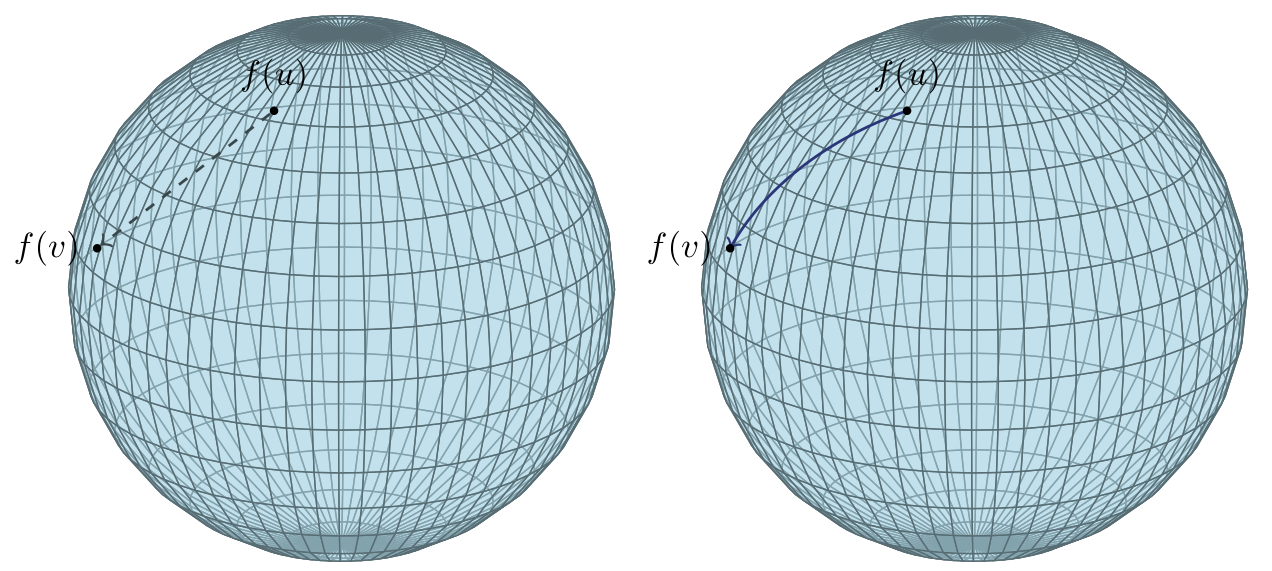
Abb. 4.1 Visualisierung zweier unterschiedlicher Abstandsbegriffe für Punkte auf der Kugeloberfläche \(\mathbb{S}^2\).¶
Aus dieser Anschauung wird klar, dass unser bisheriges Konzept von Differenzierbarkeit im Mehrdimensionalen aus dem MP-2 Skript nicht ausreicht, um auf diesem Objekt geeignet Funktionen abzuleiten. Da man in vielen Bereichen der Physik und der Mathematik nicht nur auf offenen Teilmengen des \(\R^n\) ableiten möchte, benötigen wir ein analoges Prinzip für topologische Räume \(\M := (\M, \tau)\).
Wie können wir den Ableitungsbegriff auf topologische Räume übertragen?
Die grundlegende Idee ist es, den topologischen Raum \(\M\) lokal mit einer Teilmenge des \(\R^n\) zu identifizieren. Für eine beliebige offene Teilmenge \(U\subset \M\) betrachten wir also eine Abbildung
Wir wollen fordern, dass es sich bei \(\phi\) um eine injektive Abbildung handelt, so dass eine inverse Abbildung \(\phi^{-1}\) existiert. Diese Umkehrabbildung müssen wir jedoch auf das Bild \(\phi(U) \subset \R^n\) einschränken, damit sie wohldefiniert ist. Damit erhalten wir eine lokale Bijektion \(\phi^{-1}:\phi(U)\rightarrow U\).
Betrachten wir nun eine Funktion \(f \colon \M \rightarrow \R^m\), die Punkte des topologischen Raumes auf Punkte des \(\R^m\) abbildet. Wenn wir diese Funktion differenzieren möchten, so sehen wir ein, dass die Verknüpfung
es uns erlaubt, das Problem der Ableitung in topologischen Räumen auf das Konzept der mehrdimensionalen Differentiation im \(\R^n\) zurückzuführen.
4.1.2.2. Karten und Atlanten auf topologischen Räumen¶
Um den Ableitungsbegriff auf topologischen Räumen \(\M\) formal definieren zu können, benötigen wir zusätzlich zur Bijektivität der Abbildung \(\phi \colon U \rightarrow \phi(U) \subset \R^n\) die Bedingung, dass für jede Teilmenge \(U \subset \M\) gilt,
Diese Forderung bedeutet, dass offene Teilmengen in \(U \subset \M\) gerade mit offenen Teilmengen in \(\phi(U) \subset \R^n\) identifiziert werden. Wir wollen im Folgenden beide Implikationsrichtungen diskutieren.
1. \(\phi(U)\) ist offen \(\Rightarrow U \) ist offen.
Diese Implikation ist äquivalent zur Forderung, dass Urbilder offener Mengen selbst wieder offen sind. Mit Definition 4.2 bedeutet dies wiederum, dass die Abbildung \(\phi\) stetig ist.
2. \(\phi(U)\) ist offen \(\Leftarrow U \) ist offen.
Analog zur obigen Überlegung sehen wir ein, dass diese Bedingung gerade aussagt, dass \(\phi^{-1}\) stetig ist. Diese Forderung ist nicht immer trivialerweise erfüllt.
Das folgende Beispiel zeigt, dass es tatsächlich stetige bijektive Abbildung \(\phi\) gibt, für die gilt, dass die Umkehrabbildung \(\phi^{-1}\) nicht stetig ist.
Example 4.2
Wir betrachten in diesem Beispiel die Funktion
Wir erkennen, dass \(\phi([0,2\pi)) = \S^1\) gerade der Einheitskreis ist, und dass \(\phi:[0,2\pi)\to\S^1\) bijektiv und stetig ist. Allerdings stellen wir fest, dass die Umkehrabbildung nicht stetig ist. Sei dazu \((x_i)_{i\in\N}\) eine Folge von Punkten auf dem Einheitskreis \(\S^1\), deren \(y\)-Koordinate negativ ist und die gegen den Punkt \(x = (1,0) \in \S^1\) konvergieren, d.h.,
Betrachten wir jedoch den Grenzwert der Folge von Funktionswerten \((\phi^{-1}(x_i))_{i\in I}\), so sehen wir, dass
und somit ist \(\phi^{-1}\) offensichtlich nicht stetig.
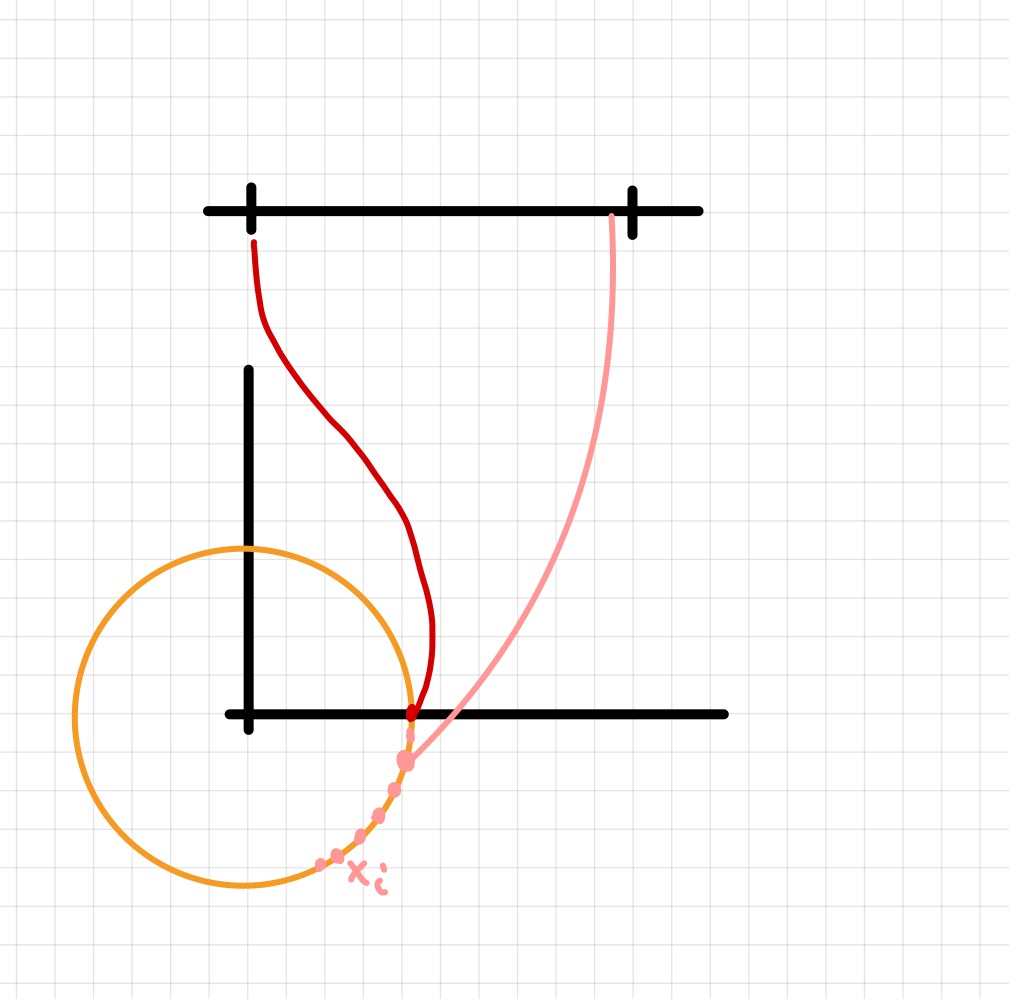
Abb. 4.2 Visualisierung einer unstetigen Umkehrabbildung für das Example 4.2.¶
Insgesamt fordern wir also, dass \(\phi:U\rightarrow\phi(U)\) bijektiv ist und zusätzlich, dass sowohl \(\phi\) als auch die Umkehrabbildung \(\phi^-1\) stetig sind. Eine solche Abbildung definiert man unter dem Begriff Homöomorphismus.
Definition 4.3 (Homöomorphismus)
Seien \(X\) und \(Y\) topologische Räume. Dann nennen wir eine Abbildung \(f \colon X \rightarrow Y\) einen Homöomorphismus, wenn sie folgende Eigenschaften erfüllt:
\(f\) ist bijektiv
\(f\) ist stetig
die Umkehrfunktion \(f^{-1}\) ist ebenfalls stetig.
Speziell im Kontext von Mannigfaltigkeiten \(\M\), als Spezialfall topologischer Räume (wie wir noch sehen werden), nennt man eine offene Menge zusammen mit einem Homöomorphismus eine Karte auf \(\M\).
Definition 4.4 (Karte)
Es sei \(\M\) ein topologischer Raum und \(U\subset\M\) eine offene Menge. Sei außerdem \(\phi:U\rightarrow \phi(U)\subset \R^n\) ein Homöomorphismus. Dann heißt das Tupel \((U,\phi)\) Karte auf \(\M\).
Um einen Ableitungsbegriff für Funktionen \(f:\M\to\R^m\) über eine Karte \((U,\phi)\) und der Verknüpfung \(f\circ \phi^{-1}\) zu definieren benötigen wir noch ein zusätzliches Konzept. Denn in der Situation, dass \((V,\psi)\) eine zweite Karte ist, deren offene Menge \(V\) einen nichtleeren Schnitt mit der offenen Menge \(U\) hat, d.h., \(U\cap V \neq \emptyset\), erhalten wir genau auf dem Schnitt dieser Mengen zwei unterschiedliche Parametrisierungen,
Um von einer Karte zur nächsten Karte zu kommen benötigen wir eine geeignete Abbildung.
Definition 4.5 (Kartenwechsel)
Es sei \(\M\) ein topologischer Raum und es seien \((U,\phi)\) und \((V,\psi)\) zwei Karten auf \(\M\) mit nicht-leerem Schnitt, d.h., \(U\cap V\neq \emptyset\). Dann nennt man die Abbildung
einen Kartenwechsel von \((U,\phi)\) nach \((V,\psi)\).
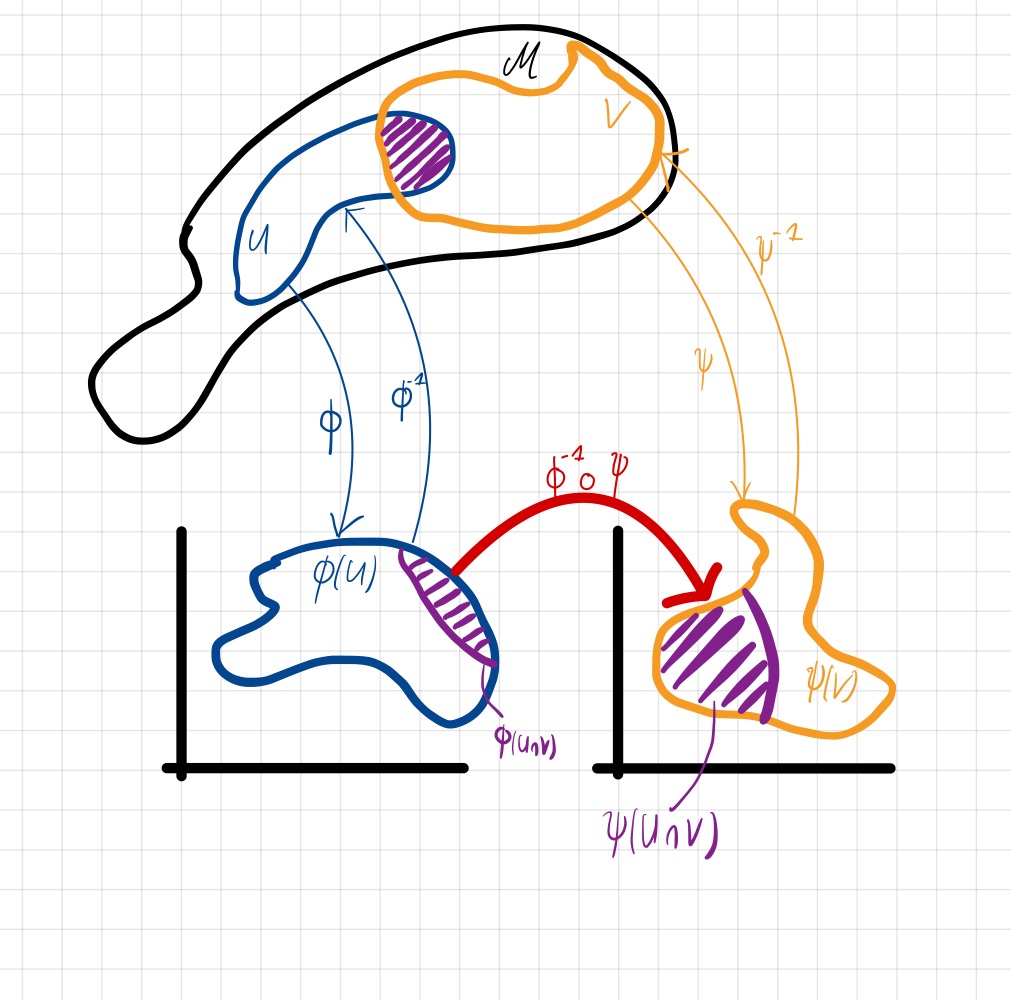
Abb. 4.3 Kartenwechsel.¶
Wir erkennen also, dass Umparametrisierungen der Form \(\psi\circ \phi^{-1}\) entscheidend sind, um von einer lokalen Identifikation des topologischen Raums zur nächsten zu gelangen. Wäre nun der Kartenwechsel \(\psi\circ \phi^{-1}\) und respektive \(\phi\circ \psi^{-1}\) differenzierbar, so könnte man die jeweiligen Ableitungen leicht durch die Kettenregel ineinander umrechnen. Allerdings existieren durchaus Beispiele, in denen sowohl \(f\circ\phi^{-1}\) als auch \(f\circ\psi^{-1}\) differenzierbar sind, aber der Kartenwechsel \(\psi\circ\phi^{-1}\) nicht. Deshalb führt man zusätzlich noch den folgenden Begriff ein.
Definition 4.6 (Atlas)
Es sei \(\M\) ein topologischer Raum. Eine Familie von Karten \(\mathcal{A} = (U_i,\phi_i)_{i\in I}\) indiziert durch die Indexmenge \(I\) heißt Atlas, falls die Vereinigung aller offenen Mengen eine Überdeckung des topologischen Raums darstellt, d.h., es gilt
Wir nennen einen Atlas \(k\)-mal differenzierbar oder von der Klasse \(C^k\), falls jeder Kartenwechsel \(\phi_i\circ\phi_j^{-1}, i,j\in I\) \(k\)-mal stetig differenzierbar ist.
Die Begriffe Karte und Atlas stammen in der Tat aus mathematischen Überlegungen in der Kartographie. Man kann Teile der Erdoberfläche mit einer Karte auf eine Ebene \(\R^2\) abbilden. Nähert man sich dem Rand einer Karte, so möchte man zu einer anderen Karte wechseln, die das angrenzende Gebiet darstellt.
So kann eine Mannigfaltigkeit durch einen vollständigen Satz von Karten vollständig beschrieben werden; man braucht dabei Regeln, wie sich beim Kartenwechsel die Karten überlappen.
4.1.2.3. Differenzierbare Mannigfaltigkeiten¶
Für einen topologischen Raum \(\M\) können mehrere Atlanten \(\mathcal{A}\) existieren, weshalb es sinnvoll ist Äquivalenzklassen von Atlanten zu betrachten.
Definition 4.7 (\(C^k\)-differenzierbare Struktur)
Für einen Index \(k\in \N \cup \{\infty\}\) heißen zwei differenzierbare Atlanten \(\mathcal{A}_1, \mathcal{A}_2\) der Klasse \(C^k\) \(k\)-äquivalent, falls ihre Vereinigung \(\mathcal{A}_1\cup \mathcal{A}_2\) wieder ein Atlas der Klasse \(C^k\) ist. Dies bedeutet insbesondere, dass die Kartenwechsel durch die Vereinigung der beiden Atlanten weiterhin \(k\)-mal stetig differenzierbar bleiben. In diesem Fall notieren wir \(\mathcal{A}_1\sim_k \mathcal{A}_2\). Die Äquivalenzklasse \([\mathcal{A}]_{\sim_k}\) nennt man eine \(C^k\)-differenzierbare Struktur.
Bisher haben wir \(\M\) als allgemeinen topologischen Raum betrachtet. In vielen Anwendungen benötigt man aber weitere nützliche Eigenschaften des Raumes. Insbesondere wenn man glatte Testfunktionen und die Zerlegung der Eins benutzen möchte braucht man folgende zwei zusätzliche Eigenschaften.
Wir definieren zunächst die Eigenschaft eines Hausdorff-Raums.
Definition 4.8 (Hausdorff-Raum)
Ein topologischer Raum \(\M\) heißt Hausdorff-Raum, falls für je zwei unterschiedliche Punkte \(x,y\in \M, x\neq y\) offene Umgebungen \(U(x), U(y) \subset \M\) existieren, welche disjunkt sind, d.h., \(U(x)\cap U(y) = \emptyset\). Man nennt \(\M\) dann auch einen separierten Raum.
Als zweite nützliche Eigenschaft fordern wir, dass unser topologischer Raum \(\M\) das zweite Abzählbarkeitsaxiom erfüllen soll.
Definition 4.9 (Zweites Abzählbarkeitsaxiom)
Ein toplogischer Raum \((\M, \tau)\) erfüllt das zweite Abzählbarkeitsaxiom, falls abzählbar viele offene Mengen \((V_i)_{i\in\N} \in \tau\) existieren, so dass für jeden Punkt \(x\in \M\) und jede offene Umgebung \(U(x) \in \tau\) von \(x\) mindestens ein Index \(k\in\N\) existiert mit \(V_k \subset U(x)\). Man nennt \((\M, \tau)\) dann auch zweitabzählbar.
Diese zwei Bedingung wirken zunächst abstrakt. Glücklicherweise werden sie jedoch von vielen üblichen topologischen Räumen erfüllt, wie zum Beispiel dem Euklidischen Raum \(\R^n\).
Remark 4.2
Falls der Begriff eines zweitabzählbaren Hausdorff-Raums zu unhandlich erscheint, kann man für die meisten Anwendungen in der Physik auch einfach metrische Räume betrachten, die diese beiden Eigenschaften implizieren.
Nun haben wir alle nötigen Voraussetzungen geschaffen um den Begriff einer Mannigfaltigkeit formal einzuführen.
Definition 4.10 (Differenzierbare Mannigfaltigkeit)
Es sei \(\M\) ein zweitabzählbarer Hausdorff-Raum und für \(k\in\N\cup \{\infty\}\) sei \([\mathcal{A}]_{\sim_k}\) eine \(C^k\)-differenzierbare Struktur. Dann nennen wir \((\M,[\mathcal{A}]_{\sim_k})\) eine \(k\)-mal differenzierbare Mannigfaltigkeit. Für den Spezialfall \(k=\infty\) sprechen wir auch von einer glatten Mannigfaltigkeit.
Falls alle Karten auf \(\M\) nach \(\R^n\) abbilden, so nennt man die Mannigfaltigkeit \(n\)-dimensional.
Ähnlich wie bei topologischen Räumen spricht man in den meisten Fällen nur von der Mannigfaltigkeit \(\M\); die differenzierbare Struktur \([\mathcal{A}]_{\sim_k}\) wird dabei implizit vorausgesetzt.
Basierend auf einer differenzierbaren Mannigfaltigkeit \(\M\) können wir nun differenzierbare Funktionen auf \(\M\) definieren.
Definition 4.11 (Differenzierbare Funktion auf einer Mannigfaltigkeit)
Sei \(\M\) eine \(k\)-mal differenzierbare Mannigfaltigkeit \(\mathcal{A}\) ein Atlas auf \(\M\). Dann nennen wir eine Abbildung \(f:\M\to\R^m\) \(k\)-mal differenzierbar, falls für jeden Punkt \(x\in\M\) eine differenzierbare Karte \((U(x),\phi)\in\mathcal{A}\) existiert, so dass \(f\circ\phi^{-1} \in C^k(\phi(U(x)); \R^m)\). Insbesondere schreiben wir in diesem Fall \(f\in C^k(\M; \R^m)\).
In vielen Anwendungen beschränkt man sich nur auf glatte Mannigfaltigkeiten und glatte Funktionen in \(C^\infty(\M; \R^m)\). Wir werden im Folgenden der Einfachheit-halber auch dazu übergehen.
Lemma 4.1
Es sei \(\M\) eine glatte Mannigfaltigkeit. Dann ist \(C^\infty(\M; \R^m)\) ein reeller Vektorraum mit den Verknüpfungen
Proof. In der Hausaufgabe zu zeigen.
Die Eigenschaft der Differenzierbarkeit einer Funktion auf einer Mannigfaltigkeit ist kartenunabhängig, wie folgendes Lemma feststellt.
Lemma 4.2 (Kartenunabhängigkeit)
Es sei \(\M\) eine glatte Mannigfaltigkeit und \(\mathcal{A}\) ein Atlas auf \(\M\). Außerdem sei \(f:\M \to \R^m\) eine Funktion, \((U,\varphi), (V,\varphi)\in \mathcal{A}\) zwei Karten mit \(x \in U\cap V\).
Dann gilt, \(f\circ\varphi^{-1}\) ist genau dann differenzierbar in \(\varphi(x)\), falls \(f\circ\psi^{-1}\) differenzierbar in \(\psi(x)\) ist.
Proof. In der Hausaufgabe zu zeigen.