Differentialformen auf Mannigfaltigkeiten
Inhalt
4.3. Differentialformen auf Mannigfaltigkeiten¶
Die vorhergehenden Abschnitte liefern nun die nötigen Grundlagen um Differentialformen zu betrachten. Insbesondere werden wir diese über eine Unterstruktur der bekannten Tensorfelder erhalten. Dieser Schritt isr konzeptionell sehr ähnlich zum Schritt von allgemeinen Tensoren zu den Antisymmetrischen, bzw. alternierenden Tensoren. Dieser Zusammenhang erklärt auch die Begrifflichkeit alternierende Differentialform welche in de Literatur häufig vorkommt.
Differentialformen sind ein wichtiges Konzept in verschieden Bereichen der Mathematik und Physik. Auch wenn wir diese Thematik hier nicht betrachten, sei erwähnt, dass Differentialformen die Integration auf speziellen glatten Mannigfaltigkeiten erlauben.
4.3.1. Differentialformen¶
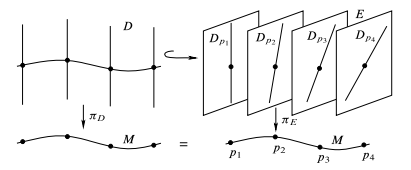
In Kapitel ?? haben wir symmetrische und antisymmetrische Tensoren kennengelernt. Dieses Konzept werden wir nun auf Tensorfelder übetragen um somit Differntialformen zu erhalten. Hierfür betrachten wir für eine glatte Mannigfaltigkeit die Menge
der alternierenden Tensorfelder. Antisymmetrische Tensoren bilden direkt eine Teilmenge aller Tensoren und es bleibt lediglich zu zeigen, dass die Vektorraumstruktur erhalten bleibt. Die Situation hier ist nun anders, man benötigt den abstrakten Begriff des Untervektorbündels.
Definition 4.31
Es seien \(\pi_E:E\to B\) und \(\pi_D:D\to B\) zwei Vektorbündel, wobei für jedes \(p\in\M\) die Untervektorraumrelation
gelte, dann heißt \(D\) Untervektorbündel von \(E\).
In diesem Fall erhält man also ein Untervektorbündel.
Lemma 4.15
Sei \(\M\) eine glatte \(n\)-dimensionale Mannigfaltigkeit, dann ist \(\Lambda^k T^\ast\M\) ein glattes Untervektorbündel vom Rang \(\begin{pmatrix} n k \end{pmatrix}\).
Proof. ToDo.
Dank der Bündelstruktur können wir erneut glatte Schnitte betrachten, welche nun auf das Konzept der Differentialform führen.
Definition 4.32
Es sei \(\M\) eine glatte Mannigfaltigkeit, dann nennt man einen glatten Schnitt
eine \(k\)-Differentialform oder auch \(k\)-Form. Den Vektorraum der Differentialformen notieren wir durch
4.3.2. Das äußere Produkt¶
In Abschnitt 3.2.6 haben wir das äußere Produkt \(\wedge\) kennengelernt, welches wir nun auf Differentialformen übertragen. Dazu seien \(\omega\in \Omega^k(\M), \eta\in \Omega^l(\M)\) zwei Differentialformen für \(k,l\in\N\), dann setzten wir
was in der Tat eine Differentialform definiert, also \(\omega\wedge\eta \in \Omega^{k+l}(\M)\). Zusätzlich überträgt sich auch die Darstellung in einer lokalen Karte von Corollary 4.2 auf diese Situation, wobei das Tensorprodukt, durch das äußere Produkt ersetzt werden kann.
Lemma 4.16
Es sei \(\M\) eine glatte Mannigfaltigkeit, \((\varphi,U)\) eine Karte und \(\omega\in\Omega^l(\M)\) eine Differentialform, dann gilt lokal in \(U\)
wobei \(\omega_{i_1\ldots i_k}\in C^\infty(\M)\) für alle \(i_1,\ldots,i_k\in\{1,\ldots,n\}\) gilts
Proof. Siehe z.B. [Lee03] Kapitel 14.
Example 4.10
1. Für \(k=0\) und \(\M\) eine glatte Mannigfaltigkeit erhalten wir
2. Für \(k=1\) und \(\M\) eine glatte Mannigfaltigkeit erhalten wir
gerade die Kovektorfelder aus Abschnitt 4.2.4.
3. Für \(k=3\) und \(\M=\R^3\) ist z.B.,
eine Differentialform.
4.3.3. Die äußere Ableitung¶
Wir wenden uns nun einer wichtigen Operation auf Differentialformen zu, der äußeren Ableitung. Aus Example 4.8 kennen wir schon das totale Differential \(df\in \Omega^1(\M)\), für eine glatte Funktion \(f\in C^\infty(\M)\). Hierbei haben wir für ein glattes Vektorfeld \(X\in \Gamma(T\M)\) die Abbildung
definiert, wobei die rechte Seite über die Wirkung des Vektorfelds definiert ist. Wir können dieses Konzept verallgemeinern, indem wir die äußere Ableitung definieren.
Definition 4.33
Es sei \(\M\) eine glatte Mannigfaltigkeit und \(f\in C^\infty(\M)\), dann definieren wir die lineare Abbildung
Remark 4.9
Beachte, dass die obige Abbildung nur jeweils für lokale Koordinaten definiert ist. Wegen der Kartenunabängigkeit führt dies aber auf eine eindeutig definierte Funktion, siehe z.B. [Lee03] Kapitel 14. Da wir \(d\) auf den Elementen \(dx^{i_1}\wedge\ldots\wedge dx^{i_k}\) definiert haben erhalten wir jeweils lokal eine eindeutige lineare Fortsetzung, da jedes \(\omega\in \Omega^k(\M)\) lokal die Darstellung
hat und somit
Example 4.11 (Äußere Ableitung)
1. Für \(\omega\in\Omega^0(\R^3)\) ist \(d\omega = \frac{\partial\omega}{\partial x_1}dx_1+ \frac{\partial\omega}{\partial x_2}dx_2+\frac{\partial\omega}{\partial x_3}dx_3\).
2. Für \(\omega = \omega_1dx_1+\omega_2dx_2+\omega_3dx_3\in\Omega^1(\R^3)\) ist
3. Für \(\omega = \omega_{12}dx_1\wedge dx_2+\omega_{23}dx_2\wedge dx_3 +\omega_{31}dx_3\wedge dx_1 \in\Omega^2(\R^3)\) ist
4. Für \(\omega\in\Omega^3(\R^3)\) ist \(d\omega=0\).
Für die äußere Ableitung können wir zusätzlich folgende Eigenschaften zeigen.
Lemma 4.17
Es sei \(\M\) eine glatte Mannigfaltigkeit, dann haben wir folgende Eigenschaften.
1. Für \(f,g\in C^\infty(\M)\) gilt
2. Für \(\omega\in\Omega^k(\M),\eta\in\Omega^l(\M)\) gilt
3. Es gilt \(d\circ d = 0\).
Remark 4.10
Da \(d\) Eigenschaft 2 erfüllt, nennt man \(d\) auch Antiderivation.
Eine interessante Anwendung finden Differntialformen im sog. Poincaré-Lemma. Hierfür benötigen wir folgenden Begriffe
Definition 4.34
Es sei \(\M\) eine glatte Mannigfaltigkeit, eine Differentialform \(v\in\Omega^k(\M)\) heißt
geschlossen, wenn \(dv=0\),
exakt, wenn \(v=d\eta\) für ein \(\eta\in\Omega^{k-1}(\M)\) gilt.
Nach Satz lem:outer:prop sind exakte Differentialformen geschlossen, da für \(v=d\eta\) gilt,
Das Poincaré-Lemma besagt nun, dass auf sternförmigen offenen Mengen \(U\subseteq \R^n\) auch die Umkehrung gilt.
Lemma 4.18 (Poincaré-Lemma)
Es sei \(U\subset\R^n\) eine offene sternförmige Menge, dann gilt für \(\omega\in \Omega^k(\M)\),
Proof. Siehe z.B. [Lee03] Theorem 11.49.
4.3.4. Der Pullback¶
Die letzte Operation die wir in diesem Kapitel betrachten ist der sogenannte Pullback. Hierbei betrachten wir zwei glatte Mannigfaltigkeiten \(\M,\mathcal{N}\) und eine glatte Funktion \(F:M\to\mathcal{N}\). Das Ziel ist es nun eine Differentialform auf \(N\), \(\omega\in\Omega^k(\mathcal{N})\) mithilfe von \(F\) auf eine Differentialform auf \(\M\) zurückzuziehen. Ausgewertet an \(p\in\M\) ergibt eine Differentialform \(\eta\in\Omega^k(\M)\) ein Element aus \(L^k(T_p\M)\), da
also eine Linearform, welche auf \(k\) Elemente \(v_1,\ldots,v_k\in T_p\M\) des Tangentialraums in \(p\) an \(\M\) wirkt. Haben wir nun a priori \(\omega\in\Omega^k(\mathcal{N})\) gegeben brauchen wir deshalb zunächst eine Methode mit der wir Tangentialvektoren über \(F\) von \(\M\) nach \(\mathcal{N}\) vorschieben können, der sogenannte Pushforward.
Definition 4.35
Es seien \(\M,\mathcal{N}\) zwei glatte Mannigfaltigkeiten und \(F\in C^\infty(\M,\mathcal{N})\), dann definieren wir für \(p\in\M\)
den sogenannten Pushforward.
Da wir nun Tangentialvektoren von \(T_p\M\) auf \(T_{F(p)}\mathcal{N}\) schieben können, sind wir in der Lage damit den Pullback von Kotangentialvektoren zu definieren.
Definition 4.36
Es seien \(\M,\mathcal{N}\) zwei glatte Mannigfaltigkeiten und \(F\in C^\infty(\M,\mathcal{N})\), dann definieren wir für \(p\in\M\)
den Pullback
Remark 4.11
Es gilt insbesondere, dass \(F^\ast v \in T_p^\ast\M\) für jedes \(v\in T_{F(p)}^\ast\mathcal{N}\).
Dieses Konzept können wir nun auf Formen übertragen in dem wir eine neue Differentialform punktweise an \(p\) definieren am Punkt \(F(p)\). Konkret seien \(v_1,\ldots, v_k\in T_p\M\), dann definiere
Die so definierte Abbildung bildet tatsächlich zwischen den passenden Räumen ab
Zusätzlich erhält man folgende Eigenschaften.
Lemma 4.19
Es seien \(\M,\mathcal{N}\) glatte Mannigfaltigkeiten und \(F\in C^\infty(\M,\mathcal{N})\), dann gilt,
\(F^\ast\) ist linear,
\(F^\ast(\omega\wedge\eta) = F^\ast(\omega) \wedge F^\ast(\eta)\) für \(\omega,\eta\in\Omega^k(\mathcal{N})\).
Für lokale Koordinaten Kovektorfelder \(dy^1,\ldots,dy^m\) und \(f\in C^\infty(\mathcal{N})\) gilt
Proof. Für 1. und 2. siehe Hausaufgaben, Für 3. siehe [Lee03] Lemma 14.16.
Im Falle, dass die Mannigfaltigkeiten gleich dem \(\R^n\) bzw. \(\R^m\) sind, also \(\M=\R^n, \mathcal{N}=\R^m\) können wir den Pullback leicht explizit berechnen. Dazu sei \(F:\R^n\to\R^m\) eine glatte Abbildung, \(x_1,\ldots,x_n\) seien Koordinaten für \(\R^n\) und \(y_1,\ldots,y_m\) seien Koordinaten für \(\R^m\).
Zunächst erkennen wir für den Pushforward, \(F_\ast:T_p\M\to T_{F(p)}\mathcal{N}\) dass für \(p\in\M\) gilt,
wobei \(\partial_i F_j\) die \(i\)-te partielle Ableitung (im klassichen Sinne) der \(j\)-ten Komponente von \(F\) ist.
Betrachten wir also den Pullback eines Kovektorfeldes \(dy^k\) ausgewertet an einem Tangentialvektor \(D\in T_p\M\)
erhalten wir unter Ausnutzung der Linearität
Da die Terme \(dy^k(\partial_{y_j})\) gleich dem Kronecker-Delta sind,
führt dies auf,
Für das äußere Produkt von \(l\) verschiedenen Kovektorfeldern \(dy^{k_1},\ldots, dy^{k_l}\) und einer glatten Funktion \(f\in C^\infty(\M)\) gilt mit Eigenschaft 2. von Lemma 4.19
Da wir die Terme \(F^\ast(dy^{k_i})\) berechnen können liefert dies ein einfaches Schema um den Pullback einer Differentialform auf \(\R^m\) zu berechnen.
Example 4.12
Es sei \(\omega\in \Omega^3(\R^4)\) eine Differentialform gegeben durch
und \(F:\R^3\to\R^4\) eine glatte Abbildung gegeben durch
Dann berechnen wir
und erhalten damit