3.2. Tensoren und Tensorprodukte¶

In diesem Kapitel widmen wir uns einem für die Physik sehr wichtigen aber relativ abstrakten Thema der Vektoranalysis, nämlich Tensoren und Tensorprodukten. Der Begriff hat sehr viele verschiedene Anschauungsmöglichkeiten (siehe Wikipedia) weshalb es nicht leicht ist eine Einführung zu geben die gleichzeitig allgemein, aber auch verständlich ist. Da Tensoren aber eine wichtige Rolle in der Physik spielen werden wir uns hier damit beschäftigen.

3.2.1. Motivation¶

Wir betrachten zunächst ein konkretes Anwendungsbeispiel aus der Physik, welches auf Tensoren zurückgreift. Hier wird der sogenannte Cauchy Spannungstensor verwendet.

Remark 3.5 (Begriffsherkunft)

Der Begriff Tensor wurde von Hamilton in der Mitte des 19. Jahrhunderts eingeführt. Er leitete die Bezeichnung vom lateinischen tendere (spannen) ab, da die ursprüngliche Anwendung derartiger Objekte in der Elastizitätstheorie Anwendung fand.

Mechanische Spannung ist eine physikalische Größe, die die innere Beanspruchung und Kräfte in einem Volumen \(V\subset\R^3\) angibt, welche aufgrund einer äußeren Belastungen auftreten. Die grundlegende Idee ist das Euler-Cauchy Spannungsprinzip, welches beschreibt, dass auf jede Schnittfläche \(A\subset\R^2\), die ein Volumen in zwei Teile trennt, von diesen zwei Volumenteilen eine Spannung auf \(A\) ausgeübt wird, welche durch einen sogenannten Spannungsvektor \(\mathbf{T}^{(n)}\) beschrieben wird. Der Komponenten des Spannungsvektors haben hierbei die Dimension „Kraft pro Fläche“.

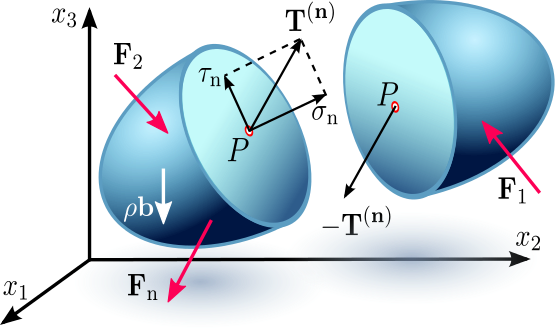
Abb. 3.1 Visualisierung für Normal- und Scherspannung an einer Schnittfläche. Quelle: Wikipedia; Cauchy Stress Tensor.¶

Wie in Abb. 3.1 visualisiert teilt sich die Spannung in zwei Komponenten auf:

Normalspannung:

Die Normalspannung \(\sigma_n\) ist der Teil des Spannungsvektors, der in Richtung der Normalen \(\mathbf{n}\) zeigt, welche orthogonal auf der Schnittfläche steht.

Scherspannung:

Die Scherspannung \(\tau_n\) ist der Teil des Spannungstensors, der parallel zur Schnittfläche liegt.

Man erkennt nun, dass die Spannung in \(V\) nicht durch einen einzigen Vektor ausgedrückt werden kann. Einerseits hängt sie vom betrachteten Punkt \(x\in V\) ab und zudem von der Orientierung der Schnittfläche. Allerdings hat Cauchy gezeigt, dass ein linearer Operator \(\mathbf{\sigma}(x)\) existiert, so dass

\[\mathbf{T}^{(n)}(x) = \mathbf{\sigma}(x) \cdot n,\]

d.h. in jedem Punkt \(x\in V\) ist der Stressvektor linear im Normalenvektor \(n\).

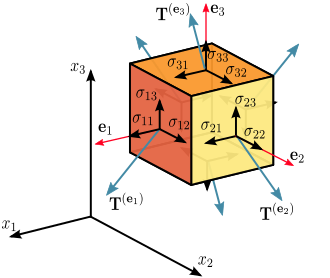
Abb. 3.2 Quelle: Wikipedia; Spannungstensor.¶

Der lineare Operator \(\mathbf{\sigma}\) wird auch Cauchy Spannungstensor genannt. Um diesen besser zu verstehen betrachtet man für einen fixen Punkt \(x\) des Volumens einen infinitesimal kleinen, freigeschnittenen Würfel wie in Abb. 3.2. Nun definieren wir für die drei verschiedenen Flächen (orthogonal zu den Einheitsvektoren \(e_1, e_2\) und \(e_3\)) die Spannungsvektoren

\[\mathbf{T}^{(e_i)}:= \sum_{j=1}^3 \sigma_{ij} e_j, \quad i \in \lbrace 1,2,3 \rbrace.\]

So setzt sich beispielsweise der Spannungsvektor \(\mathbf{T}^{(e_1)}\) zusammen aus der Summe der Normalspannung \(\sigma_{11} e_1\) und den zwei Scherspannungskomponenten \(\sigma_{12} e_2\) und \(\sigma_{13} e_3\).

Insgesamt erhält man neun Spannungskomponenten \(\sigma_{ij}\) für \(i,j=1,2,3\) welche insgesamt den Spannungszustand im Punkt \(x\) als Spannungsvektoren in Richtung der Einheitsvektoren vollständig beschreiben. Dies liegt daran, dass wir jeden Spannungsvektor in \(x\) als Linearkombination der drei Spannungsvektoren \(\mathbf{T}^{(e_i)}, i=1,2,3\) darstellen können.

Wir führen nun eine multilineare Abbildung \(\otimes \colon \R^n \times \R^m \rightarrow \R^{n \times m}\) für zwei beliebige Vektoren \(x\in\R^n\) und \(y\in\R^m\) ein, die das dyadische Produkt der Vektoren genannt wird und wie folgt definiert ist

\[\begin{split}x \otimes y := \begin{pmatrix} x_1y_1 &\ldots &x_1 y_m\\ \vdots &\ddots & \vdots\\ x_n y_1&\ldots& x_n y_m \end{pmatrix}.\end{split}\]

Fassen wir nun zeilenweise die Spannungsvektoren \(\mathbf{T}^{(e_i)}, i=1,2,3\) in einer Matrix zusammen, so erhalten wir den Cauchy Spannungstensor \(\mathbf{\sigma}\) für den Punkt \(x\) des Volumens als

(3.1)¶\[\begin{split}\mathbf{\sigma} := \begin{pmatrix} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33} \end{pmatrix} &= \begin{pmatrix} \mathbf{T}^{(e_1)} \\ \mathbf{T}^{(e_2)} \\ \mathbf{T}^{(e_3)} \end{pmatrix} = \begin{pmatrix} \mathbf{T}^{(e_1)} \\ 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ \mathbf{T}^{(e_2)} \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ \mathbf{T}^{(e_3)} \\ \end{pmatrix}\\ &= \sum_{i=1}^3 e_i \otimes \mathbf{T}^{(e_i)} = \sum_{i=1}^3 e_i\otimes ( \sum_{j=1}^3 \sigma_{ij} e_j) = \sum_{i=1}^3\sum_{j=1}^3 \sigma_{ij} (e_i\otimes e_j).\end{split}\]

Wir werden später sehen, dass man die Idee, den Operator \(\sigma\) über das dyadische Produkt zu definieren, abstrahieren kann, was auf den allgemeinen Tensorbegriff führt.

Remark 3.6

In der Tat handelt es sich bei dem Operator \(\sigma \colon \R^3 \rightarrow \R^3\) in (3.1) nicht nur um einen Tensor, sondern genauer um ein Tensorfeld, dass jedem Punkt \(x\) des Volumens einen Spannungstensor zuordnet.

3.2.2. Das Tensorprodukt¶

Wir wollen nun das Tensorprodukt von Vektorräumen abstrakt einführen und es an späterer Stelle für konkrete Realisierungen diskutieren. Hierbei wollen wir uns zunächst auf einen Spezialfall einschränken, der lediglich zwei Vektorräume berücksichtigt, um die zu Grunde liegenden wichtigen Konzepte klarer herauszustellen. Es ist wichtig zu verstehen, dass die folgenden Definitionen sich mit dem Konzept der \(k\)-Multilinearität in Multilinearformen auf \(k \in \N\) verschiedene \(\R\)-Vektorräume direkt verallgemeinern lassen.

Definition 3.4 (Tensorprodukt)

Es seien \(V\) und \(W\) zwei reelle Vektorräume. Ein reeller Vektorraum \(X\) heißt Tensorproduktraum falls eine bilineare Abbildung \(\otimes:V\times W\rightarrow X\) existiert, so dass die folgende universelle Eigenschaft gilt:

Für jede Bilinearform \(\phi\in L^2(V\times W; Y)\) in einen beliebigen reellen Vektorraum \(Y\), existiert eine eindeutige lineare Abbildung \(p \in L^1(X; Y)\), so dass gilt

(3.2)¶\[\phi(v,w) = p(v\otimes w) = p(\otimes(v,w))\quad\forall (v,w)\in V\times W.\]

In diesem Fall schreibt man auch \(X = V \otimes W\). Wir nennen die bilineare Abbildung \(\otimes\) Tensorprodukt und verwenden häufig für sie die Infix-Schreibweise \(v\otimes w := \otimes(v,w)\). Elemente \(x \in X\) des Tensorproduktraums \(X = V \otimes W\) nennen wir Tensoren.

Diese Definition erscheint auf den ersten Blick abstrakt und unverständlich. Was ist jetzt also genau ein Tensorprodukt?

Das Tensorprodukt ist universell:

Wir haben in der Definition 3.4 das kartesische Produkt \(\times\) benutzt welches eindeutig definiert ist. Im Gegensatz dazu gibt es jedoch nicht ein Tensorprodukt \(\otimes\) oder einen Tensorproduktraum \(V\otimes W\). Wir haben die Freiheit \(\otimes\) zu wählen und wann immer die universelle Eigenschaft erfüllt ist, heißt dann \(X = V\otimes W\) Tensorproduktraum. Derartige Konzepte nennt man in der Algebra universell. Betrachten wir hierzu ein kurzes Beispiel für unterschiedliche Realisierungen eines Tensorproduktes.

Example 3.5 (Varianten eines Tensorprodukts)

Wir betrachten in diesem Beispiel den Euklidischen Vektorraum \(V=W=\R^2\) und zwei Vektoren \(x, y \in \R^2\). Nehmen wir zunächst das Tensorprodukt, dass durch das dyadische Produkt \(\otimes : \R^2 \times \R^2 \rightarrow \R^{2 \times 2}\) gegeben ist mit

\[\begin{split}x \otimes y \, \coloneqq \, \begin{pmatrix} x_1y_1 & x_1y_2 \\ x_2y_1 & x_2y_2 \end{pmatrix}.\end{split}\]

Man sieht ein, dass der zugehörige Tensorproduktraum also \(\R^{2 \times 2} = \R^2 \otimes \R^2\) sein muss. Anderseits erhält man den gleichen Tensorproduktraum, wenn man ein alternatives Tensorprodukt \(\otimes^*\) zum dyadischen Produkt definiert, welches lediglich die Reihenfolge der Komponenten von \(y\) vertauscht mit

\[\begin{split}x \otimes^* y \, \coloneqq \, \begin{pmatrix} x_1y_2 & x_1y_1 \\ x_2y_2 & x_2y_1 \end{pmatrix}.\end{split}\]

Was bedeutet die universelle Eigenschaft?

Wie wir weiter unten noch genauer beschreiben werden, stellt die universelle Eigenschaft eine wichtige Beziehung zwischen dem Raum der bilinearen Abbildungen auf \(V\times W\) und dem Raum der linearen Abbildungen von \(X = V\otimes W\) nach \(Y\) für ein Tensorprodukt \(\otimes\) her. Für den Spezialfall \(Y = \R\) ist letzterer gerade der algebraische Dualraum des Tensorproduktraums. Sofern wir das Tensorprodukt gegeben haben erhalten wir alle Bilinearformen also schon über einfache Linearformen auf \(V\otimes W\).

Das folgende einfache Beispiel soll uns helfen diese Beziehung besser zu verstehen.

Example 3.6 (Universelle Eigenschaft)

Im Folgenden betrachten wir wieder den Euklidischen Vektorraum \(V=W=\R^2\) und zwei Vektoren \(x, y \in \R^2\). Wie wir in Example 3.5 festgestellt haben realisiert das dyadische Produkt

\[\otimes \colon \R^2 \times \R^2 \rightarrow \R^2 \otimes \R^2 = \R^{2 \times 2} =: X\]

mit

\[\begin{split}x \otimes y \, \coloneqq \, \begin{pmatrix} x_1y_1 & x_1y_2 \\ x_2y_1 & x_2y_2 \end{pmatrix}.\end{split}\]

ein Tensorprodukt der Vektorräume \(V=W=\R^2\). Wegen der universellen Eigenschaft muss nun gelten, dass für jede Bilinearform \(\Phi \in L^2(V \times W; Y)\) für beliebige \(\R\)-Vektorräume \(Y\) eine eindeutige lineare Abbildung \(p \in L^1(X; Y)\) existiert, die äquivalent im Sinne von (3.2) ist.

Nehmen wir also beispielsweise das Skalarprodukt \(\langle \cdot, \cdot \rangle \colon V \times W \rightarrow \R\) als eine mögliche Bilinearform \(\Phi \in L^2(V \times W; Y)\) mit

\[\langle x, y \rangle = x^T \cdot y = x_1y_1 + x_2y_2.\]

Wir müssen nun einen linearen Operator \(p \in L^1(X; Y)\) finden, der eine äquivalente Berechnung wie das Skalarprodukt auf dem Tensorproduktraum \(X = \R^{2 \times 2}\), der durch das dyadische Produkt induziert wird, durchführt. Hierzu wählen wir die Spur \(p(A) \coloneqq \operatorname{Spur}(A)\) einer Matrix \(A \in \R^{2 \times 2}\), denn diese ist linear und es gilt:

\[\begin{split}\operatorname{Spur} \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} = a_{11} + a_{22}.\end{split}\]

Überprüfen wir mit dieser Wahl nun die universelle Eigenschaft des dyadischen Produkts, so erhalten wir

\[\begin{split}\Phi(x,y) = \langle x, y \rangle = x_1y_1 + x_2y_2 = \operatorname{Spur} \begin{pmatrix} x_1y_1 & x_1y_2 \\ x_2y_1 & x_2y_2 \end{pmatrix} = \operatorname{Spur}(x \otimes y) = p(x \otimes y).\end{split}\]

Es sei angemerkt, dass wir nicht gezeigt haben, dass der Spur-Operator der einzige lineare Operator ist, der diese Äquivalenz erfüllt. Betrachten wir statt dessen die alternative Variante \(\otimes^*\) des dyadischen Produkts aus Example 3.5, so bleibt der Tensorproduktraum gleich, jedoch ändert sich der eindeutig bestimmte, lineare Operator \(p \in L^1(X; Y)\). Durch die Vertauschung der Elemente der Matrix \(x \otimes^* y\) nimmt man nicht mehr die Summe der Hauptdiagonalelemente realisiert durch den Operator \(\operatorname{Spur}(A) = a_{11} + a_{22}\), sondern die Summe der Gegendiagonalelemente realisiert durch einen linearen Operator \(\operatorname{Spur}^*(A) \coloneqq a_{21} + a_{12}\), d.h., die Diagonale von links unten nach rechts oben in der Matrix. In diesem Fall erhält man nämlich analog

\[\begin{split}\Phi(x,y) = \langle x, y \rangle = x_1y_1 + x_2y_2 = \operatorname{Spur}^* \begin{pmatrix} x_1y_2 & x_1y_1 \\ x_2y_2 & x_2y_1 \end{pmatrix} = \operatorname{Spur}^*(x \otimes^* y) = p(x \otimes^* y).\end{split}\]

Dies Veranschaulicht die Beziehung der involvierten Vektorräume und die zu Grunde liegende universelle Eigenschaft des Tensorprodukts.

Gefahr

Wir haben in Example 3.6 lediglich die universelle Eigenschaft zur Veranschaulichung überprüft für ein konkretes Beispiel. Wir haben jedoch nicht gezeigt, dass das dyadische Produkt die universelle Eigenschaft erfüllt. Dafür hätten wir die Äquivalenz für alle möglichen Bilinearformen \(\Phi \in L^2(V \times W; Y)\) für beliebige Vektorräume \(Y\) beweisen müssen.

3.2.3. Existenz und Konstruktion des Tensorprodukts¶

Wir stellen fest, dass es für zwei beliebige \(\R\)-Vektorräume \(V\) und \(W\) immer ein Tensorprodukt gibt, und dass wir dieses Tensorprodukt konkret konstruieren können indem wir uns auf die Basis der Vektorräume \(V\) und \(W\) zurückziehen. Diese Tatsache formulieren wir in der folgenden Aussage.

Theorem 3.1 (Existenz des Tensorprodukts)

Für zwei reelle Vektorräume \(V, W\) existiert stets mindestens ein Tensorprodukt \(\otimes\in L^2(V\times W; V\otimes W)\).

Proof. Der folgende Beweis ist ein sogenannter konstruktiver Beweis, d.h., wir zeigen die Existenz eines Objekts indem wir es explizit angeben. Im Gegensatz hierzu gibt es auch nicht-konstruktive Existenzbeweise.

Es sei \(B^V = \{b_i^V: i\in I^V\}\) eine Basis von \(V\) und es sei analog \(B^W = \{b_i^W: i\in I^W\}\) eine Basis von \(W\) für zwei Indexmengen \(I^V\) und \(I^W\). Wir betrachten zunächst das kartesische Produkt der beiden Indexmengen

\[J := I^V \times I^W = \{(i,j): i\in I^V, j\in I^W\}.\]

Es sei nun \(X\) ein reeller Vektorraum dessen Basis sich durch \(J\) indizieren lässt, das heißt es existiert eine Menge

\[B^X = \{b_{ij}^X: (i,j)\in J\},\]

so dass \(B^X\) eine Hamel-Basis von \(X\) ist. Man kann zeigen, dass ein solcher Vektorraum immer existiert.

Wir definieren nun eine bilineare Abbildung \(\otimes: V\times W \to X\) über

\[\otimes (b_i^V, b_j^W) = b_i^V \otimes b_j^W := b_{ij}^X \quad \forall (i,j)\in J.\]

Es sei darauf hingewiesen, dass die bilineare Abbildung \(\otimes\) durch eine Definition über die Indexmenge \(J\) eindeutig festgelegt ist. Dies liegt daran, dass für beliebige Paare \((v,w)\in V\times W\) endlich viele Koeffizienten \(\alpha_{i_1},\ldots,\alpha_{i_n}\) und \(\beta_{j_1},\ldots, \beta_{j_m}\) existieren, so dass für die Vektoren \(v \in V\) und \(w \in W\) eine Darstellung in den jeweiligen Hamel-Basen existiert mit

\[v = \sum_{k=1}^n \alpha_{i_k} b_{i_k}^V, \quad w = \sum_{l=1}^m \beta_{j_l} b_{j_l}^W.\]

Durch diese Darstellung erhalten wir für die bilineare Abbildung \(\otimes: V\times W \to X\) nun eine explizite Vorschrift als

\[\otimes(v,w) = \otimes\big(\sum_{k=1}^n \alpha_{i_k} b_{i_k}^V, \sum_{l=1}^m \beta_{j_l} b_{j_l}^W\big) = \sum_{k=1}^n \sum_{l=1}^m \alpha_{i_k} \beta_{j_l} \otimes\left(b_{i_k}^V, b_{j_l}^W\right) = \sum_{k=1}^n \sum_{l=1}^m \alpha_{i_k} \beta_{j_l} b_{i_kj_l}^X.\]

Wir müssen nun noch die universelle Eigenschaft der bilinearen Abbildung \(\otimes\) nachweisen, um zu zeigen, dass es sich um ein Tensorprodukt handelt. Sei dazu \(\phi\in L^2(V\times W; Y)\) eine Bilinearform auf einen beliebigen reellen Vektorraum \(Y\). Dann können wir eine Linearform auf \(p: X\to Y\) explizit definieren durch Angabe ihrer Wirkung auf die Basiselemente mit

\[p(b_{ij}^X) := \phi(b_i^V, b_j^W) \quad \forall (i,j) \in J.\]

Dann gilt nämlich, unter Ausnutzung der Linearität von \(p\) und der obigen Rechnung, dass gilt

\[\begin{split}p(\otimes(v,w)) &= p \left( \sum_{k=1}^n \sum_{l=1}^m \alpha_{i_k} \beta_{j_l} b_{i_kj_l}^X \right) = \sum_{k=1}^n \sum_{l=1}^m \alpha_{i_k} \beta_{j_l} p(b_{i_kj_l}^X) \\ &= \sum_{k=1}^n \sum_{l=1}^m \alpha_{i_k} \beta_{j_l} \phi\left(b_{i_k}^V, b_{j_l}^W\right) = \phi\big(\sum_{k=1}^n \alpha_{i_k} b_{i_k}^V,\sum_{l=1}^m \beta_{j_l} b_{j_l}^W\big) = \phi(v,w)\end{split}\]

Wir sehen also, dass \(\otimes\) die universelle Eigenschaft erfüllt und zwar insbesondere dadurch, dass die Linearform \(p\) durch die obige Definition eindeutig festgelegt ist.

Als Korollar aus Theorem 3.1 erhalten wir somit, dass eine Basis des Tensorproduktraums durch das kartesische Produkt der ursprünglichen Basen konstruiert werden kann. Hieran sieht man den qualitativen Unterschied zwischen \(V \times W\) und \(V\otimes W\).

Corollary 3.1

Für zwei reelle Vektorräume \(V\) und \(W\) mit zugehörigen Hamel-Basen

\[B^V = \{b_i^V: i\in I^V\}, \quad B^W = \{b_i^W: i\in I^W\},\]

und einem Tensorprodukt \(\otimes:V\times W \to V\otimes W\) ist

\[B^X \, \coloneqq \, \{b_i^V \otimes b_j^W: i\in I^V, j\in I^W\}\]

eine Basis von \(X = V\otimes W\).

Wir wissen nun aus Theorem 3.1, dass immer mindestens ein Tensorprodukt existiert. Es stellt sich also die Frage inwiefern sich verschiedene Tensorprodukte auf den gleichen Vektorräumen \(V\) und \(W\) unterscheiden. Hierzu liefert das folgende Lemma eine klare Einsicht.

Lemma 3.4 (Isomorphie von Tensorprodukträumen)

Es seien \(V\) und \(W\) zwei reelle Vektorräume und es seien

\[\begin{split}\otimes_1 &\colon V \times W \rightarrow V \otimes_1 W,\\ \otimes_2 &\colon V \times W \rightarrow V \otimes_2 W\end{split}\]

zwei Tensorprodukte. Dann existiert genau ein Isomorphismus

\[p: V\otimes_1 W \to V\otimes_2 W,\]

so dass gilt \(\otimes_2 = p\circ \otimes_1\).

Proof. Seien also zunächst zwei Tensorprodukte \(\otimes_1, \otimes_2\) auf \(V\times W\) gegeben. Wegen der universellen Eigenschaft des Tensorprodukts wissen wir, dass es lineare Abbildungen

\[\begin{split}p_1&: V\otimes_1 W\to Y_1 \ \coloneqq \ V\otimes_2 W,\\ p_2&: V\otimes_2 W\to Y_2 \ \coloneqq \ V\otimes_1 W\end{split}\]

gibt, so dass gilt

\[\begin{split}\otimes_2 &= p_1 \circ \otimes_1,\\ \otimes_1 &= p_2 \circ \otimes_2.\end{split}\]

Durch Einsetzen der Gleichungen ineinander somit

\[\begin{split}\otimes_2 &= p_1\circ p_2 \circ \otimes_2,\\ \otimes_1 &= p_2\circ p_1 \circ \otimes_1.\end{split}\]

Aus dem Beweis von Theorem 3.1 wissen wir, dass wir die Basis von \(V\otimes_2 W\) über die Abbildung \(\otimes_2(b_i^V, b_j^W)\) der Basiselemente von \(V\) und \(W\) charakterisieren können. Setzen wir also das Tensorprodukt dieser Basiselemente in die erste Gleichung ein, so erhalten wir

\[\otimes_2(b_i^V, b_j^W) = p_1\circ p_2(\otimes_2(b_i^V,b_j^W)).\]

Das zeigt also, dass \(p_1\circ p_2 = \mathrm{Id}_{Y_1}\) die Identitätsabbildung auf dem Tensorproduktraum \(Y_1 = V \otimes_2 W\) sein muss. Dies folgt, weil \(p_1\circ p_2\) als lineare Abbildung schon ganz durch seine Wirkung auf den Basiselementen festgelegt ist. Analog kann man nun folgern, dass \(p_2\circ p_1 = \mathrm{Id}_{Y_2}\) die Identitätsabbildung im Tensorproduktraum \(Y_2 = V \otimes_1 W\) ist und somit sind die Linearformen \(p_1\) und \(p_2\) Isomorphismen und gerade die jeweiligen Umkehrfunktionen zueinander.

Insgesamt haben wir also gezeigt, dass Tensorprodukträume, die durch verschiedene Tensorprodukte auf dem gleiche kartesischen Produkraum stets isomorph zueinander sind.

Im endlich-dimensionalen Fall können wir uns also immer auf den \(\R^{n \cdot m}\) zurückziehen, wie das folgende Korrolar festhält.

Corollary 3.2

Betrachten wir ein Tensorprodukt \(\otimes \in L^2(V \times W; V \otimes W)\) zweier endlich-dimensionaler \(\R\)-Vektorräume \(V\) und \(W\) mit \(\operatorname{dim}(V)=n \in \N\) und \(\operatorname{dim}(W)=m \in \N\), so existiert stets die folgende Isormorphie

\[V \otimes W \cong \R^{n \cdot m}.\]

Das heißt für die Dimension des Tensorproduktraums \(V \otimes W\) gilt offensichtlich

\[\operatorname{dim}(V \otimes W) = n\cdot m.\]

Das folgende Beispiel soll noch einmal die Isomorphie zwischen verschiedenen Tensorprodukträumen illustrieren.

Example 3.7 (Dyadisches Produkt vs. Kronecker-Produkt)

Im Folgenden betrachten wir wieder den Euklidischen Vektorraum \(V=W=\R^2\) und zwei Vektoren \(x, y \in \R^2\). Wie wir in Example 3.5 und Example 3.6 festgestellt haben realisiert das dyadische Produkt

\[\otimes_d \colon \R^2 \times \R^2 \rightarrow \R^2 \otimes_d \R^2 = \R^{2 \times 2} =: X_d\]

mit

\[\begin{split}x \otimes_d y \, \coloneqq \, \begin{pmatrix} x_1y_1 & x_1y_2 \\ x_2y_1 & x_2y_2 \end{pmatrix}.\end{split}\]

ein Tensorprodukt der Vektorräume \(V=W=\R^2\).

Betrachten wir nun ein weiteres Tensorprodukt auf dem kartesischen Produktraum \(V \times W\), nämlich das Kronecker-Produkt \(\otimes_K\).

Das Kronecker-Produkt realisiert eine Abbildung

\[\otimes_K \colon \R^2 \times \R^2 \rightarrow \R^2 \otimes_K \R^2 = \R^{4} =: X_K,\]

mit

\[\begin{split}x \otimes_K y = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \otimes_K \begin{pmatrix} y_1 \\ y_2 \end{pmatrix} \, = \, \begin{pmatrix} x_1 \cdot \begin{pmatrix} y_1 \\ y_2 \end{pmatrix} \\ x_2 \cdot \begin{pmatrix} y_1 \\ y_2 \end{pmatrix} \end{pmatrix} = \begin{pmatrix} x_1y_1\\ x_1y_2\\ x_2y_1\\ x_2y_2 \end{pmatrix}.\end{split}\]

Es wird nun klar, dass die Räume \(X_d = \R^{2 \times 2}\) und \(X_K = \R^4\) isomorph zueinander sind, d.h., es gilt \(X_d \cong X_K\). Außerdem kann man Tensoren in den jeweiligen Tensorprodukträumen durch zeilenweises Ablesen bzw. Eintragen in eine Matrix eindeutig ineinander überführen.

Das Tensorprodukt?

Die Aussage aus Lemma 3.4 zeigt also, dass obwohl es verschiedene Arten gibt Tensorprodukte auf dem kartesischen Produktraum \(V \times W\) zu definieren, die resultierenden Tensorprodukträume stets isomorph zueinander sind. Deshalb spricht man auch von dem Tensorprodukt \(\otimes\) und dem Tensorproduktraum \(V \otimes W\), was so klingt als gäbe es jeweils nur ein einziges Exemplar. In der Tat gibt es zwar mehrere Tensorprodukte aber man kann diese problemlos ineinander umrechnen und die resultierenden Tensorprodukträume alle miteinander identifizieren.

Deshalb werden wir im Folgendem auch häufig von dem Tensorprodukt sprechen.

3.2.4. Natürliche Homo- und Isomorphismen des Tensorprodukts¶

Von vielen Operationen kennen wir bereits Eigenschaften wie Kommutativität und Assoziativität. Derartige Eigenschaften gelten nicht direkt für das Tensorprodukt, allerdings erhalten wir Isomorphismen, welche bekannte Rechenregeln nachbilden. Diese Isomorphismen nennt auch natürlich oder kanonisch, weil Sie jeweils auf die naheliegendste Art und Weise definiert sind. Das folgende Lemma fasst die wichtigsten Eigenschaften des Tensorprodukts zusammen

Lemma 3.5 (Natürliche Isomorphismen des Tensorprodukts)

Es seien \(V_1,V_2,V_3\) und \(V_4\) reelle Vektorräume. Dann existieren für das Tensorprodukt die folgenden Isomorphismen:

\(V_1\otimes V_2 \cong V_2\otimes V_1, \quad v_1\otimes v_2 \mapsto v_2\otimes v_1\) (Kommutativität),
\((V_1\otimes V_2)\otimes V_3 \cong V_1 \otimes (V_2 \otimes V_3),\quad (v_1\otimes v_2)\otimes v_3 \mapsto v_1 \otimes (v_2\otimes v_3)\) (Assoziativität),
\(\R \otimes V_1 \cong V_1,\quad a\otimes v_1 \mapsto a\,v_1\) (Produkt mit Skalaren),
Falls \(p_{12}:V_1\to V_2\) und \(p_{34}:V_3\to V_4\) Isomorphismen sind, so gilt (Transitivität)

\[V_1\otimes V_3 \cong V_2\otimes V_4,\quad v_1\otimes v_3 \mapsto p_{12}(v_1)\otimes p_{34}(v_3)\]

Proof. Punkt 1.-3. sind in der Hausaufgabe zu zeigen.

Zu Punkt 4.:

Wichtig für die Transitivitätseigenschaft ist es zunächst einzusehen, dass die Definition des Tensorprodukts sinnvoll ist, denn nicht jedes Element \(x\in V_1\otimes V_3\) lässt sich direkt als Tensorprodukt schreiben. Wir wissen lediglich, dass endlich viele sogenannte elementare oder zerfallende Produkte \((v_1^i\otimes v_3^i)_{i=1}^n\) und Skalare \(\alpha_i\in\R, i=1,\ldots,n\), für \(n\in\N\) existieren, so dass sich jeder Vektor \(x \in V_1 \otimes V_3\) schreiben lässt als

\[x = \sum_{i=1}^n \alpha_i (v_1^i \otimes v_3^i),\]

was direkt aus der Basiskonstruktion in Theorem 3.1 folgt.

Die angegebene Abbildung

\[v_1\otimes v_3 \mapsto p_{12}(v_1)\otimes p_{34}(v_3)\]

ist nun nur für zerfallende Produkte definiert. Allerdings lässt sie sich eindeutig zu einer linearen Abbildung \(\Phi(V_1\otimes V_3)\to (V_2\otimes V_4)\) fortsetzen, so dass für beliebige Vektoren \(x \in V_1 \otimes V_3\) gilt

\[\Phi(x) = \Phi(\sum_{i=1}^n \alpha_i v_1^i \otimes v_3^i) = \sum_{i=1}^n \alpha_i \Phi(v_1^i \otimes v_3^i) = \sum_{i=1}^n \alpha_i (p_{12}(v_1^i)\otimes p_{34}(v_3^i)).\]

Auf analoge Art und Weise definiert man nun die lineare Abbildung \(\Psi \colon V_2 \otimes V_4 \rightarrow V_1 \otimes V_3\) mit

\[\Psi(v_2\otimes v_4) := p_{12}^{-1}(v_2)\otimes p_{34}^{-1}(v_4)\]

und erhält sofort, dass \(\Psi\circ\Phi = \mathrm{Id}\) gilt, da für beliebige Vektoren \(x \in V_1 \otimes V_3\) gilt:

\[\begin{split}\Psi \circ \Phi(x) &= \Psi \circ \Phi(\sum_{i=1}^n \alpha_i v_1^i \otimes v_3^i) = \Psi \circ \sum_{i=1}^n \alpha_i (p_{12}(v_1^i)\otimes p_{34}(v_3^i)) \\ &= \sum_{i=1}^n \alpha_i \Psi(p_{12}(v_1^i)\otimes p_{34}(v_3^i)) = \sum_{i=1}^n \alpha_i (v_1^i \otimes v_3^i) = x.\end{split}\]

Analog gilt auch \(\Phi\circ\Psi = \mathrm{Id}\) und somit haben wir die Behauptung des Lemmas bewiesen.

Die zweite Eigenschaft in Lemma 3.5 erlaubt es uns das Tensorprodukt über \(k\)-viele reelle Vektorräume \(V_1,\ldots, V_k\) zu bilden. Daher können wir ab nun folgende Notation verwenden

\[\bigotimes_{i=1}^k V_i :=V_1\otimes\ldots\otimes V_k\]

und sehen, dass dieses Objekt wohldefiniert ist. Insbesondere ist äquivalent das Tensorprodukt über \(k\) Vektorräume mit Hilfe einer \(k\)-Multilinearform aus k-Multilinearformen zu definieren anstatt nur einer Bilinearform wie in Definition 3.4. Die folgende Bemerkung gibt die universelle Eigenschaft für solch ein Tensorprodukt an.

Remark 3.7 (\(k\)-faches Tensorprodukt)

Es seien \(V_1,\ldots, V_k\) für \(k \in \N\) reelle Vektorräume. Dann besitzt das \(k\)-fache Tensorprodukt \(\otimes \colon V_1 \times \ldots \times V_k \rightarrow \bigotimes_{i=1}^k V_i\) die folgende universelle Eigenschaft:

Für jede \(k\)-Multilinearform \(\phi\in L^k(V_1\times\ldots\times V_k; Y)\) in einen beliebigen reellen Vektorraum \(Y\) existiert eine eindeutige lineare Abbildung \(p \in L^1(\bigotimes_{i=1}^k V_i; Y)\), so dass gilt

\[\phi = p \circ \otimes.\]

Remark 3.8 (Notation)

Im obigen Fall interpretiert man \(\otimes: V_1\times\ldots\times V_k \rightarrow \bigotimes_{i=1}^k V_i\) als \(k\)-Multilinearform und benutzt die Infix-Notation

\[v_1\otimes\ldots\otimes v_k := \otimes(v_1,\ldots, v_k).\]

Im folgenden Abschnitt der Vorlesung wollen wir Tensoren insbesondere als Multilinearformen interpretieren. Deshalb interessieren wir uns im Folgenden für die Eigenschaften des Tensorprodukts, wenn wir speziell Räume von linearen Abbildungen betrachten. Die lineare Abbildung im folgenden Lemma stellt hierbei die zentrale Idee dar.

Lemma 3.6

Es seien \(V_1, V_2\) sowie \(W_1, W_2\) reelle Vektorräume. Dann ist die Abbildung

\[\begin{split}p:L(V_1; V_2)\otimes L(W_1; W_2) &\rightarrow L(V_1\otimes W_1; V_2\otimes W_2)\\ (p(\eta_1\otimes\eta_2))(v_1\otimes w_1)&:= \eta_1(v_1) \otimes \eta_2(w_1).\end{split}\]

ein wohldefinierter Homomorphismus.

Proof. In der Hausaufgabe zu zeigen.

Da die Notation in Lemma 3.6 vielleicht etwas abstrakt wirkt, soll die folgende Bemerkung auf die einzelnen Elemente der linearen Abbildung \(p\) nochmal genauer eingehen.

Remark 3.9 (Funktionen als Funktionswerte)

Die lineare Abbildung in Lemma 3.6 ist folgendermaßen zu verstehen:

\(\eta_1:V_1\rightarrow V_2\) und \(\eta_2: W_1 \rightarrow W_2\) sind lineare Abbildungen mit \(\eta_1 \in L(V_1; V_2)\) und \(\eta_2 \in L(W_1; W_2)\)
\(\eta_1 \otimes \eta_2\) ist dementsprechend ein Element aus dem Tensorproduktraum \(L(V_1; V_2)\otimes L(W_1; W_2)\),
\(p(\eta_1\otimes\eta_2)\) ist dann ein Element von \(L(V_1\otimes W_1; V_2\otimes W_2)\), also eine lineare Abbildung, welche vom Tensorproduktraum \(V_1\otimes W_1\) in den Tensorproduktraum \(V_2\otimes W_2\) abbildet,
\((p(\eta_1\otimes\eta_2))(v_1\otimes w_1)\) ist schließlich die Auswertung dieser Abbildung am Punkt \(v_1\otimes w_1\in V_1\otimes W_1\).

In diesem Fall notiert man auch

\[\eta_1\otimes\eta_2 \mapsto \big[ v_1\otimes w_1\mapsto \eta_1(v_1) \otimes \eta_2(w_1) \big],\]

was bedeutet, dass \(\eta_1\otimes\eta_2\) auf eine Funktion abgebildet wird, welche wiederum \(v_1\otimes w_1\) als Argumente bekommt.

Insbesondere können wir im endlich-dimensionalen Fall zeigen, dass die Abbildung \(p\) in Lemma 3.6 einen Isomorphismus definiert. Hierzu formulieren wir zunächst das folgende nützliche Hilfslemma.

Lemma 3.7

Seien \(V\) und \(W\) zwei beliebige reelle Vektorräume und \(n,m \in \N\). Dann existiert ein Isomorphismus, so dass

\[(V \otimes W)^{n\cdot m} \cong V^n \otimes W^m.\]

Proof. In der Hausaufgabe zu zeigen.

Theorem 3.2

Es seien \(V_1, W_1\) reelle endlich-dimensionale Vektorräume und \(V_2, W_2\) beliebige reelle Vektorräume. Dann ist die Abbildung

\[\begin{split}p:L(V_1; V_2)\otimes L(W_1; W_2) &\rightarrow L(V_1\otimes W_1; V_2\otimes W_2)\\ (p(\eta_1\otimes\eta_2))(v_1\otimes w_1)&:= \eta_1(v_1) \otimes \eta_2(w_1).\end{split}\]

ein Isomorphismus.

Proof. Seien \(V_1\) und \(W_1\) zwei endlich-dimensionale, reelle Vektorräume mit \(\operatorname{dim}(V_1) = n \in \N\) und \(\operatorname{dim}(W_1) = m \in \N\). Nach dem Isomorphiesatz für endlich-dimensionale Vektorräume 3.20 in [Bur20] existiert dann je ein Isomorphismus, so dass \(V_1 \cong \R^n\) und \(W_1 \cong \R^m\). Über diesen Isomorphismus lässt sich auch zeigen, dass \(L(V_1; V_2) \cong L(\R^n; V_2)\) und \(L(W_1; W_2) \cong L(\R^m; W_2)\) gilt. Zusammen mit der Transitivitätseigenschaft des Tensorprodukts aus Lemma 3.5 folgt dann aber schon

\[L(V_1; V_2)\otimes L(W_1; W_2) \cong L(\R^n; V_2)\otimes L(\R^m; W_2).\]

Daher reicht es, die Aussage des Theorems für den einfachen Fall \(V_1=\R^n, W_1=\R^m\) im Folgenden in zwei Schritten zu zeigen.

1.Schritt: Wir zeigen zunächst, dass die Isomorphie \(L(\R^k; Y) \cong Y^k\) gilt.

Es sei \(Y\) ein beliebiger reeller Vektorraum und es bezeichne \((e_i)_{i=1}^k\) die Standardbasis von \(\R^k\). Wir konstruieren nun eine Abbildung \(\phi:Y^k\rightarrow L(\R^k; Y)\), so dass

\[\phi(y_1,\ldots,y_k) = [e_i \mapsto y_i], \quad i = 1,\ldots,k\]

gilt. Die Abbildung \(\phi\) ist linear, da für alle Vektoren \(y,z \in Y^k\) und einen beliebigen Vektor \(x \in \R^k\) mit der Basisdarstellung \(x=\sum_{i=1}^k \alpha_i e_i\) gilt:

\[\begin{split}\phi(y+z)(x) &= \phi(y_1+z_1,\ldots, y_k+z_k)(\sum_{i=1}^k \alpha_i e_i) = \sum_{i=1}^k \alpha_i (y_i + z_i) \\ &= \sum_{i=1}^k \alpha_i y_i + \sum_{i=1}^k \alpha_i z_i = \phi(y_1,\ldots, y_k)(\sum_{i=1}^k \alpha_i e_i) + \phi(z_1,\ldots, z_k)(\sum_{i=1}^k \alpha_i e_i) \\ &= \phi(y)(x) + \phi(z)(x)\end{split}\]

und für jedes Skalar \(\lambda \in \R\) gilt:

\[\begin{split}\phi(\lambda y)(x) &= \phi(\lambda y_1,\ldots, \lambda y_k)(\sum_{i=1}^k \alpha_i e_i) = \sum_{i=1}^k \alpha_i (\lambda y_i) = \lambda \sum_{i=1}^k \alpha_i y_i \\ &= \lambda \phi( y_1,\ldots, y_k)(\sum_{i=1}^k \alpha_i e_i) = \lambda \phi(y)(x).\end{split}\]

Offenbar ist diese lineare Abbildung auch injektiv, denn

\[\phi(y_1,\ldots,y_k)(e_i) = 0\quad\forall i\in{1,\ldots k} \qquad \Leftrightarrow \qquad y_i = 0\quad\forall i\in{1,\ldots k}.\]

Gleichzeitig ist die lineare Abbildung jedoch auch surjektiv, da jede lineare Abbildung in \(L(\R^k; Y)\) sich bereits durch seine Wirkung auf den Basiselementen \(e_i \in \R^k, i=1,\ldots,k\) eindeutig beschreiben lässt.

Wir sehen also ein, dass es sich bei der Abbildung \(\phi\) um einen Isomorphismus handelt und somit gilt also \(L(\R^k; Y) \cong Y^k\).

2.Schritt: Als Nächstes wollen wir die folgenden Isomorphien zeigen:

\[L(\R^n; V_2) \otimes L(\R^m; W_2) \cong V_2^n \otimes W_2^m\cong L(\R^n\otimes \R^m; V_2\otimes W_2).\]

Mit Schritt 1 des Beweises wissen wir bereits, dass \(L(\R^n; V_2)\cong V_2^n\) und \(L(\R^m; W_2)\cong W_2^m\) gilt. Zusammen mit der Transitivitätseigenschaft des Tensorprodukts aus Lemma 3.5 folgt damit schon die erste Isomorphie

(3.3)¶\[L(\R^n; V_2) \otimes L(\R^m; W_2) \cong V_2^n \otimes W_2^m.\]

Für die zweite Isomorphie benutzen wir den Zusammenhang \(\R^n\otimes \R^m \cong \R^{n\cdot m}\) aus Corollary 3.2 und erhalten somit

\[L(\R^n\otimes \R^m; V_2\otimes W_2) \cong L(\R^{n\cdot m}; V_2\otimes W_2).\]

Nutzen wir wiederum die Isomorphie aus Schritt 1 so erhalten wir

\[L(\R^{n\cdot m}; V_2\otimes W_2) \cong (V_2 \otimes W_2)^{n\cdot m}.\]

Wegen Lemma 3.7 wissen wir dann aber schon, dass gilt

\[(V_2 \otimes W_2)^{n\cdot m} \cong V_2^n \otimes W_2^m.\]

Zusammen mit der Isomorphie (3.3) haben wir nun insgesamt gezeigt, dass

\[L(\R^n; V_2) \otimes L(\R^m; W_2) \cong L(\R^n\otimes \R^m; V_2\otimes W_2)\]

gilt, was mit unseren Vorüberlegungen die Aussage des Theorems beweist.

Wählen wir die Zielräume der linearen Abbildungen als \(V_2 = W_2 = \R\), so erhalten wir direkt folgendes Korrolar als Anwendung des allgemeinen Resultats in Theorem 3.2. Dies ermöglicht es uns später Tensoren als Linearformen zu interpretieren.

Corollary 3.3 (Isomorphie des algebraischen Dualraums des Tensorproduktraums)

Es seien \(V\) und \(W\) beliebige endlich-dimensionale Vektorräume. Dann existiert ein Isomorphismus zwischen dem Tensorproduktraum der algebraischen Dualräume von \(V\) und \(W\) und dem algebraischen Dualraum des Tensorproduktraums, d.h.,

\[V^\ast \otimes W^\ast \cong (V\otimes W)^\ast = L^1(V \otimes W; \R).\]

3.2.5. Tensoren als Multilinearformen¶

Das folgende Korollar kombiniert die theoretischen Ergebnisse des letzten Abschnitts und liefert so ein mathematisches Resultat, das für die Anwendung beispielsweise in der Physik von Bedeutung ist. Wir werden nämlich nun folgern, dass wir Tensoren als Multilinearformen auffassen können.

Corollary 3.4 (Tensoren als Multilinearformen)

Seien \(V\) und \(W\) zwei reelle endlich-dimensionale Vektorräume und \(\otimes \colon V \times W \rightarrow V \otimes W\) das Tensorprodukt. Dann existiert ein Isomorphismus zwischen dem Tensorproduktraum und dem Raum der Bilinearformen durch

\[V \otimes W \cong L^2(V \times W; \R).\]

Proof. Wie wir in Corollary 3.3 gesehen haben, besteht ein Isomorphismus zwischen dem Tensorproduktraum algebraischer Dualräume und dem algebraischen Dualraum des entsprechenden Tensorproduktraums mit

\[V^\ast \otimes W^\ast \cong (V\otimes W)^\ast = L^1(V \otimes W; \R).\]

Da jeder endlich-dimensionale, reelle Vektorraums \(V\) nach Lemma 3.3 isomorph zu seinem algebraischen Dualraum \(V^\ast\) ist, können wir die Transitivitätseigenschaft des Tensorprodukts aus Lemma 3.5 ausnutzen und erhalten die folgende Isomorphie

(3.4)¶\[V \otimes W \cong V^\ast \otimes W^\ast.\]

Gleichzeitig besagt die universelle Eigenschaft des Tensorprodukts in , dass es zu jeder Bilinearform \(\Phi \in L^2(V \times W; \R)\) eine eindeutige Linearform \(p \in L^1(V \otimes W; \R)\) gibt, so dass \(\Phi = p \circ \otimes\) gilt. Somit erhalten wir also auch einen Isomorphismus

\[L^1(V \otimes W; \R) \cong L^2(V \times W; \R).\]

Kombinieren wir diese mathematischen Resultate nun alle so ergibt sich die folgende Kette von Isomorphismen:

\[V \otimes W \cong V^\ast \otimes W^\ast \cong L^1(V \otimes W; \R) \cong L^2(V \times W; \R),\]

was die Aussage beweist.

Corollary 3.4 besagt, dass Tensoren als Elemente des Tensorproduktraums \(V \otimes W\) als Bilinearformen auf dem kartesischen Produktraum \(V \times W\) aufgefasst werden können. Diese Aussage lässt sich mit Hilfe von Remark 3.7 auch auf das \(k\)-fache Tensorprodukt verallgemeinern. Hier erhält man dann das Resultat, dass sich Tensoren als \(k\)-Multilinearformen interpretieren lassen mit

\[\V_1\otimes\ldots\otimes\V_k \cong L^k(\V_1\times\ldots\times\V_k;\R) \cong L(\V_1\otimes\ldots \otimes\V_k;\R).\]

In (3.4) haben wir die Transitivitätseigenschaft des Tensorprodukts ausgenutzt, um beide Vektorräume mit ihren jeweiligen algebraischen Dualräumen zu identifizieren. Dies muss jedoch nicht sein, denn wir hätten genauso gut gemischte Tensorprodukte der Form \(V \otimes W^\ast\) oder \(V^\ast \otimes W\) betrachten können, wenn wir die triviale Identifikation \(V \cong V\) oder \(W \cong W\) nutzen. Daher wollen wir im Folgenden Tensoren einer allgemeineren Form betrachten, nämlich solche, die für kartesische Produkte der Form \(V^r\times (V^\ast)^s\) mit \(r+s=k\) definiert sind.

Definition 3.5 (Gemischte Tensoren)

Es sei \(V\) ein reeller endlich-dimensionaler Vektorraum und \(V^\ast\) der zugehörige algebraische Dualraum. Dann nennt man

\[T^r_s(V) := L^k(V^r\times (V^\ast)^s; \R)\]

für \(k = r+s \in \N\) die Menge der gemischten Tensoren, welche kovariant der Stufe \(r\) und kontravariant der Stufe \(s\) sind. In manchen Kontexten spricht man auch nur von gemischten Tensoren der Stufe \(k=r+s\).

Die folgende Bemerkung erklärt, woher die Begriffe Kovarianz und Kontravarianz stammen.

Remark 3.10 (Ko- und Kontravarianz)

Die Bezeichnungen „kovariant“ und „kontravariant“ beziehen sich auf die Koordinatendarstellungen von Tensoren. Genauer gesagt beschreieb Sie, wie sich solche Koordinatendarstellungen bezüglich eines Basiswechsels im zugrundeliegenden Vektorraum verhalten.

Zusammenfassend kann man festhalten:

Kovariant nennt man ein Transformationsverhalten, bei dem sich die Basisvektoren und die darin dargestellten Größen in gleicher Weise transformieren.
Kontravariant nennt man ein Transformationsverhalten, wenn sich die Basisvektoren und die darin dargestellten Größen in unterschiedlicher Weise transformieren.

Das folgende Beispiel gibt eine Intuition für den Begriff der Kontravarianz an Hand von Vektorkoordinaten unter Basiswechseloperationen.

Example 3.8

Sei \(V = \R^3\) der Euklidische Vektorraum und sei

\[\begin{split}B_1 := \lbrace \begin{pmatrix}1\\ 0\\ 0\end{pmatrix}, \begin{pmatrix}0\\ 1\\ 0\end{pmatrix}, \begin{pmatrix}0\\ 0\\ 1\end{pmatrix} \rbrace\end{split}\]

die Standard-Einheitsbasis des \(\R^3\). Sei nun \(x \in \R^3\) ein Vektor, dessen Koordinaten bezüglich der Basis \(B_1\) gegeben sind als

\[\begin{split}x = \begin{pmatrix}4\\ 8\\ 2\end{pmatrix}.\end{split}\]

Führen wir nun einen Basiswechsel von \(B_1\) zu einer neuen Basis \(B_2\) mit

\[\begin{split}B_2 := \lbrace \begin{pmatrix}2\\ 0\\ 0\end{pmatrix}, \begin{pmatrix}0\\ 2\\ 0\end{pmatrix}, \begin{pmatrix}0\\ 0\\ 2\end{pmatrix} \rbrace\end{split}\]

durch, so ändert sich die Koordinatendarstellung von \(x\) bezüglich dieser Transformation zu

\[\begin{split}x = \begin{pmatrix}2\\ 4\\ 1\end{pmatrix}.\end{split}\]

Wir sehen also, dass durch die Skalierung der Basisvektoren von \(B_1\) um den Faktor \(2\) sich die entsprechende Koordinatendarstellung halbiert, d.h., sich gerade gegensätzlich zur Basistransformation verhält. Daher sind Vektoren kontravariant bezüglich Basiswechseltransformationen.

Wir wollen diese allgemeine Definition von gemischten Tensoren nun mit einfachen Beispielen veranschaulichen. Beginnen wir zunächst mit dem Spezialfall von rein kovarianten Tensoren.

Example 3.9 (Rein kovariante Tensoren)

Sei \(V\) ein endlich-dimensionaler, reeller Vektorraum mit \(\operatorname{dim}(V) = n \in \N\). Wir wollen im Folgenden Tensoren unterschiedlicher Stufen betrachten, die Multilinearformen repräsentieren. Diese haben keine kontravarianten Komponenten, sind also sozusagen rein kovariant.

Stufe 0: Wir betrachten Tensoren der Stufe \(r+s=0+0=0\). Elemente der Menge \(T^0_0(V) = L^0(V^0; \R)\) sind gerade die Skalare des zu Grunde liegenden Körpers \(\R\), da der Vektorraum \(V^0\) nur das Nullelement enthält.

Stufe 1: Wir betrachten Tensoren der Stufe \(r+s=1+0=1\). In diesem Fall entsprechen Elemente der Menge \(T^1_0(V) = L^1(V; \R)\) gerade den Linearformen des Vektorraums \(V\). Genauer gesagt handelt es sich um Elemente des algebraischen Dualraums \(V^\ast\).

Stufe k: Wir betrachten Tensoren der Stufe \(r+s=k+0=k\) für \(k\in \N\). Diese Tensoren entsprechen gerade den \(\mathbf{k}\)-Multilinearformen, da \(T^k_0(V) = L^k(V^k; \R) = L^k(V; \R)\).

Stufe n: Wir betrachten Tensoren der Stufe \(r+s=n+0=n\). Ein Beispiel für Elemente der Menge \(T^n_0(V) = L^n(V^n; \R)\) ist die Determinante einer \(n \times n\)-Matrix.

Betrachten wir als Nächstes den Spezialfall von rein kontravarianten Tensoren.

Example 3.10 (Rein kontravariante Tensoren)

Sei \(V\) ein endlich-dimensionaler, reeller Vektorraum. Diese besitzen keine kovarianten Komponenten, sind also sozusagen rein kontravariant.

Stufe 1: Wir betrachten Tensoren der Stufe \(r+s=0+1=1\). In diesem Fall entsprechen Elemente der Menge \(T^0_1(V) = L^1(V^\ast; \R)\) gerade den Vektoren des Vektorraums \(V\). Genauer gesagt handelt es sich um Elemente des Bidualraums \(V^{**}\), der nach Remark 3.4 isomorph zu \(V\) ist.

Stufe 2: Wir betrachten Tensoren der Stufe \(r+s=0+2=2\). In diesem Fall entsprechen Elemente der Menge \(T^0_2(V) = L^2(V^\ast \times V^\ast; \R)\) sogenannten Bivektoren oder Dyaden. Ein Beispiel hierfür sind Tensoren, die durch dyadische Produkte erzeugt werden.

Abschließend betrachten wir noch ein Beispiel für echt gemischte Tensoren.

Example 3.11 (Echt gemischte Tensoren)

Sei \(V\) ein endlich-dimensionaler, reeller Vektorraum. Wir wollen im Folgenden echt gemischte Tensoren diskutieren. Diese besitzen sowohl kontravariante als auch kovariante Komponenten.

Wir betrachten echt gemischte Tensoren der Stufe \(r+s=1+1=2\). Die Menge \(T^1_1(V) = L^2(V^\ast \times V; \R)\) enthält dann alle linearen Abbildung, die einer Linearform und einem Vektor eine reelle Zahl zuweisen. Ein typisches Beispiel für solch einen ist die sogenannte duale Paarung

\[\begin{split}\langle \cdot, \cdot \rangle \colon V^\ast \times V &\rightarrow \R,\\ (L, v) &\mapsto \langle L, v \rangle := L(v).\end{split}\]

Hier wird ein gegebener Vektor \(v \in V\) durch einen gegebenen linearen Operator \(L \in V^\ast\) ausgewertet. Die duale Paarung stellt eine Verallgemeinerung des Skalarprodukts dar.

3.2.6. Symmetrie und Antisymmetrie von Tensoren¶

Oft spielen gerade in der Physik spezielle Familien von Tensoren eine wichtige Rolle, nämlich symmetrische und antisymmetrische Tensoren. Diese Operatoren zeichnen sich durch ihr Verhalten unter Vertauschung von Argumenten aus und werden besonders in der Quantenmechanik und Kontinuumsmechanik betrachtet.

Bevor wir die Symmetrieeigenschaften von Tensoren definieren können, benötigen wir weitere Hilfsmittel aus der Kombinatorik. Die Vertauschung von Argumenten entspricht einer Permutationsabbildung und daher wollen wir das Vorzeichen solch einer Permutation betrachten, welches die Symmetrieeigenschaften von Tensoren charakterisiert.

Definition 3.6 (Signum einer Permutation)

Sei \(k\in\N\) und \(\pi \colon \lbrace 1,\ldots, k\rbrace \rightarrow \lbrace 1,\ldots, k\rbrace\) eine Permutation der Indizes \(1,\ldots,k\). Dann bezeichnen wir mit \(\operatorname{sgn}(\pi) := (-1)^{|\operatorname{inv}(\pi)|}\) das sogenannte Signum der Permutation \(\pi\), für das man die Menge der Fehlstände der Permutation \(\operatorname{inv}(\pi)\) betrachtet mit:

\[\operatorname{inv}(\pi) := \lbrace i,j \in \lbrace 1, \ldots, k \rbrace : i < j, \pi(i) > \pi(j) \rbrace.\]

Remark 3.11 (Signum durch Transpositionen)

Man erhält eine äquivalente Definition indem man die Darstellung einer Permuattaion durch Transpositionen betrachtet. Eine Permuation vertauscht genau zwei Zahlen, konkret, definiert man für \(r,l\in\{1,\ldots,k\}\) die Permutation \(\tau_{rl}:\{1,\ldots,k\}\to\{1,\ldots,k\}\) wie folgt,

\[\begin{split}\tau_{rl}(i) = \begin{cases} l&\text{ falls } i=r,\\ r&\text{ falls } i=l,\\ i\text{ sonst} \end{cases}.\end{split}\]

Jede Permutation lässt sich als Verkettung von Nachbarvertauschung darstellen, also Permutationen von benachbarten Elemneten. Konkret gilt für \(r<l\),

\[\tau_{rl} = \underbrace{\left(\tau_{l-1,l}\circ\ldots\circ \tau_{r+1,r+2} \right)}_{\text{Element }r\text{ nach vorne durchreichen}}\circ \underbrace{\left(\tau_{r,r+1}\circ\ldots\circ \tau_{l-1,l} \right)}_{\text{Elemnet }l\text{ nach hinten durchreichen}}\]

und da jede Nachbarvertauschung einen Fehlstand produziert gilt

\[|\operatorname{inv}\tau_{rl}| = (l-r) + (l-r-1) = 2(l-r)-1\]

was stets ungerade ist und somit haben wir \(\operatorname{sgn}(\tau_{rl}) = -1\) für belibiebige Transpositionen ungleich der Identität. Sei \(\pi\) nun eine Permutation und \(M(\pi)\) die Anzahl der Transpostionen mit welcher wir \(\pi\) darstellen können, dann gilt

\[\operatorname{sgn}(\pi) = -1^{M(\pi)}.\]

Das folgende einfache Beispiel illustriert die Berechnung des Signums einer Permutation.

Example 3.12 (Signum zweier Permutationen)

Wir betrachten im Folgenden zwei verschiedene Permutationen

\[\pi_i \colon \lbrace 1, 2, 3, 4 \rbrace \rightarrow \lbrace 1, 2, 3, 4 \rbrace \quad i=1,2.\]

1. Sei die Permutation \(\pi_1\) gegeben mit

\[\pi_1(1) = 3, \quad \pi_1(2) = 2, \quad \pi_1(3) = 4, \quad \pi_1(4) = 1.\]

Für die Menge der Fehlstände \(\operatorname{inv}(\pi_1)\) selektieren wir diejenigen Elemente \(i,j \in \lbrace 1,2,3,4 \rbrace\) mit \(i < j\) und \(\pi(i) > \pi(j)\). Dies trifft auf folgende Paare von Elementen zu:

\[\operatorname{inv}(\pi_1) = \lbrace (1,2), (1,4), (2,4), (3,4)\rbrace.\]

Da die Permutation \(\pi_1\) insgesamt \(4\) Fehlstände erzeugt, gilt für das Signum der Permutation:

\[\operatorname{sgn}(\pi_1) := (-1)^{|\operatorname{inv}(\pi_1)|} = (-1)^4 = +1.\]

2. Sei die Permutation \(\pi_2\) gegeben mit

\[\pi_1(1) = 2, \quad \pi_1(2) = 4, \quad \pi_1(3) = 1, \quad \pi_1(4) = 3.\]

Für die Menge der Fehlstände \(\operatorname{inv}(\pi_2)\) selektieren wir diejenigen Elemente \(i,j \in \lbrace 1,2,3,4 \rbrace\) mit \(i < j\) und \(\pi(i) > \pi(j)\). Dies trifft auf folgende Paare von Elementen zu:

\[\operatorname{inv}(\pi_2) = \lbrace (1,3), (2,3), (2,4)\rbrace.\]

Da die Permutation \(\pi_2\) insgesamt \(3\) Fehlstände erzeugt, gilt für das Signum der Permutation:

\[\operatorname{sgn}(\pi_2) := (-1)^{|\operatorname{inv}(\pi_2)|} = (-1)^3 = -1.\]

Nun sind wir in der Lage die Symmetrieeigenschaften von Tensoren formal zu definieren.

Definition 3.7 (Symmetrie und Antisymmetrie von Tensoren)

Sei V ein reeller, endlich-dimensionaler Vektorraum und \(T \in T_k^0(V)\) ein rein kontravarianter Tensor von Stufe \(k \in \N\).

Wir nennen den Tensor \(T\) symmetrisch, wenn für alle möglichen Permutationen \(\pi \colon \lbrace 1,\ldots, k\rbrace \rightarrow \lbrace 1,\ldots, k\rbrace\) der Indizes \(1,\ldots,k\) der Wert des Tensors mit permutierten Argumenten sich nicht ändert, d.h.,

\[T(v_1, \ldots, v_k) = T(v_{\pi(1)}, \ldots, v_{\pi(k)}).\]

Wir nennen den Tensor \(T\) antisymmetrisch oder schiefsymmetrisch, wenn für alle möglichen Permutationen \(\pi \colon \lbrace 1,\ldots, k\rbrace \rightarrow \lbrace 1,\ldots, k\rbrace\) der Indizes \(1,\ldots,k\) der Wert des Tensors mit permutierten Argumenten sich bis auf das Vorzeichen nicht ändert und dabei folgendem Zusammenhang genügt

\[T(v_1, \ldots, v_k) = \operatorname{sgn}(\pi) \cdot T(v_{\pi(1)}, \ldots, v_{\pi(k)}).\]

In Definition 3.7 haben wir die Symmetrieeigenschaften für rein kontravariante Tensoren eingeführt. Analog lässt sich die (Anti-)Symmetrie eines rein kovarianten Tensors \(T \in T^k_0(V)\) von Stufe \(k\) definieren. Die Definition von Symmetrie bzw. Antisymmetrie von echt gemischten Tensoren aus Definition 3.5 ist hingegen wenig sinnvoll, da die Rechenvorschrift eine gemischten Tensors unter beliebigen Permutationen der Argumente nicht mehr wohldefiniert sein muss.

Im folgenden Beispiel diskutieren wir jeweils einen Vertreter für symmetrische und antisymmetrische Tensoren.

Example 3.13 (Symmetrieeigenschaften von Tensoren)

Betrachten wir zunächst das Standardskalarprodukt

\[\langle \cdot, \cdot \rangle \colon \R^n \times \R^n \rightarrow \R\]

als rein kontravarianten Tensor zweiter Stufe. Da das Standardskalarprodukt im \(\R^n\) eine positiv definite, symmetrische Bilinearform ist, überträgt sich die Symmetrieeigenschaft auf die Interpretation als Tensor. Daher ist das Standardskalarprodukt ein symmetrischer Tensor.

Als zweites Beispiel betrachten wir das sogenannte Levi-Civita-Symbol, auch genannt Epsilon-Tensor,

\[\begin{split}\epsilon_{i_1,\ldots,i_n} := \begin{cases} \operatorname{sgn}((i_1,\ldots,i_n))&\text{ falls }(i_1,\ldots,i_n)\text{ eine Permutation beschreibt,}\\ 0&\text{ sonst,} \end{cases}\end{split}\]

welcher einem Tupel von \(n\in\N\) Indizes \((i_1,\ldots,i_n) \in \N^n\) einen Wert zuordnet, je nachdem ob eine gerade oder eine ungerade Anzahl an Vertauschung benötigt wird, um die Indizes in aufsteigender Reihenfolge zu sortieren. Wird eine gerade Anzahl an Vertauschungen benötigt, so gilt \(\epsilon_{i_1,\ldots,i_n} = +1\). Wird eine ungerade Anzahl an Vertauschungen benötigt, so gilt \(\epsilon_{i_1,\ldots,i_n} = -1\). Aus letzterer Vorschrift lässt sich ableiten, dass der Epsilon-Tensor den Wert \(0\) haben muss, wenn mindestens zwei der Indizes gleich sind. Dies unterscheidet das Levi-Civita-Symbol vom Signum einer Permutation in Definition 3.6, welche als Bijektion auf paarweise verschiedenen Indizes definiert ist.

Aus dieser Vorschrift lässt sich bereits direkt ableiten, dass es sich beim Levi-Civita-Symbol um einen antisymmetrischen Tensor n-ter Stufe handelt, da jede paarweise Vertauschung von Indizes das Vorzeichen des Tensors wechselt.

Es stellt sich heraus, dass die Menge der (anti-)symmetrischen Tensoren eine Vektorraumstruktur induzieren, wie das folgende Lemma zeigt.

Lemma 3.8 (Vektorraum der (anti-)symmetrischen Tensoren)

Sei \(V\) ein endlich-dimensionaler, reeller Vektorraum mit \(\operatorname{dim}(V) = n \in \N\) und sei \(k \in \N\) mit \(k \leq n\). Seien außerdem

\[\Lambda_k(V) = \lbrace \omega \in T_k^0(V) : \omega \text{ ist antisymmetrisch} \rbrace.\]

die Menge der antisymmetrischen Tensoren der Stufe \(k\) auf \(V\) und

\[\mathcal{S}_k(V) = \lbrace \omega \in T_k^0(V) : \omega \text{ ist symmetrisch} \rbrace.\]

die Menge der symmetrischen Tensoren der Stufe \(k\) auf \(V\).

Dann bilden \(\Lambda_k(V)\) und \(\mathcal{S}_k(V)\) bezüglich der Addition von Tensoren und der skalaren Multiplikation in \(\R\) einen reellen Vektorraum.

Proof. In der Hausaufgabe zu zeigen.

Abschließend wollen wir uns in diesem Abschnitt noch einem nützlichen mathematischen Werkzeug widmen, das es erlaubt beliebige Tensoren symmetrisch bzw. antisymmetrisch zu machen. Hierzu definieren wir die folgenden Projektionsabbildungen.

Definition 3.8 (Fermionische und bosonische Projektion)

Sei \(V\) ein beliebiger, reeller Vektorraum und \(k \in \N\). Wir definieren zunächst die sogenannte fermionische Projektion

\[\begin{split}\Pi_- \colon T_k^0(V) &\rightarrow \Lambda_k(V), \\ T(v_1, \ldots, v_k) &\mapsto (\Pi_- T)(v_1, \ldots, v_k) := \frac{1}{k!} \sum_{\pi \in S_k} \operatorname{sgn}(\pi) \, T(v_{\pi(1)}, \ldots, v_{\pi(k)}).\end{split}\]

Diese Projektionsabbildung weist jedem Tensor \(T\in T_k^0\) der Stufe \(k\) einen antisymmetrischen Tensor \(\Pi_-(T) \in \Lambda_k(V)\) zu.

Analog definieren wir die sogenannte bosonische Projektion

\[\begin{split}\Pi_+ \colon T_k^0(V) &\rightarrow \mathcal{S}_k(V), \\ T(v_1, \ldots, v_k) &\mapsto (\Pi_+ T)(v_1, \ldots, v_k) := \frac{1}{k!} \sum_{\pi \in S_k} T(v_{\pi(1)}, \ldots, v_{\pi(k)}).\end{split}\]

Diese Projektionsabbildung weist jedem Tensor \(T\in T_k^0\) der Stufe \(k\) einen symmetrischen Tensor \(\Pi_+(T) \in \mathcal{S}_k(V)\) zu.

Remark 3.12

Die Bezeichnung fermionisch und bosonisch in Definition 3.8 stammen daher, dass symmetrische Tensorprodukte identische Bosonen in der Quantenmechanik beschreiben, wohingegen antisymmetrische Tensorprodukte identischen Fermionen zugeordnet werden. Weitere Informationen findet man beispielsweise unter Ununterscheidbarkeit von Teilchen in der Quantenmechanik.

3.2.7. Grassmann-Algebra¶

Im letzten Abschnitt haben wir gesehen, dass die Menge der antisymmetrischen Tensoren von Stufe zusammen mit der Addition von Tensoren der gleichen Stufe einen Vektorraum \(\Lambda_k(V)\) bildet. Im Folgenden werden wir sehen, dass wir sogar noch mehr Struktur in Form einer Algebra erhalten, wenn wir den Vektorraum mit einer verträglichen Multiplikation von Tensoren erweitern.

Zunächst wollen wir das äußere Produkt zweier Tensoren definieren.

Definition 3.9 (Äußeres Produkt von Tensoren)

Sei \(V\) ein endlich-dimensionaler, reeller Vektorraum und seien \(r,r',s,s' \in \N\). Sei außerdem \(T \in T^r_s(V)\) ein Tensor, der kovariant von Stufe \(r\) und kontravariant von Stufe \(s\) ist und sei \(T' \in T^{r'}_{s'}(V)\) ein Tensor, der kovariant von Stufe \(r'\) und kontravariant von Stufe \(s'\) ist.

Dann wird das äußere Tensorprodukt von \(T\) und \(T'\) (manchmal auch Tensormultiplikation genannt) als folgende Abbildung definiert:

\[\begin{split}(T \otimes T')(v_1,\ldots,v_r,v'_1,\ldots,v'_{r'},&w_1,\ldots,w_s,w'_1,\ldots,w'_{s'}) := \\ &T(v_1,\ldots,v_r,w_1,\ldots,w_s)\cdot T'(v'_1,\ldots,v'_{r'},w'_1,\ldots,w'_{s'}).\end{split}\]

Wir sehen also, dass das Tensorprodukt von Tensoren unterschiedlicher Stufe eine Abbildung induziert, die per Definition einen Tensor höherer Stufe liefert, d.h.,

\[\otimes : T^r_s(V) \times T^{r'}_{s'}(V) \rightarrow T^{r+r'}_{s+s'}(V),\]

Mit Hilfe des äußeren Produkts von Tensoren in Definition 3.9 sind wir nun in der Lage ein äußeres Produkt für antisymmetrische Tensoren zu definieren.

Definition 3.10 (Äußeres Produkt von antisymmetrischen Tensoren)

Sei \(V\) ein endlich-dimensionaler, reeller Vektorraum mit \(\operatorname{dim}(V) = n\) und seien \(\Lambda_k(V), \Lambda_l(V)\) jeweils die Vektorräume der antisymmetrischen Tensoren der Stufe \(k\in\N\) und \(l\in\N\). Wir definieren das sogenannte äußere Produkt als die folgende Abbildung

\[\begin{split}\wedge : \Lambda_k(V) \times \Lambda_l(V) &\rightarrow \Lambda_{k+l}(V),\\ (\omega, \eta) &\mapsto \wedge(\omega,\eta) = \frac{(k+l)!}{k! \, l!} \Pi_-(\omega \otimes \eta).\end{split}\]

Häufig wird für das äußere Produkt die Infix-Notation verwendet, d.h., \(\omega \wedge \eta := \wedge(\omega,\eta)\).

Das folgende Lemma fasst die wichtigsten Eigenschaften des äußeren Produkts von antisymmetrischen Tensoren zusammen.

Lemma 3.9 (Eigenschaften des äußeren Produkts)

Sei \(V\) ein endlich-dimensionaler, reeller Vektorraum und \(\lambda \in \R\) ein Skalar. Seien außerdem folgende antisymmetrische Tensoren gegeben: \(\omega, \omega' \in \Lambda_k(V), \eta \in \Lambda_l(V), \tau \in \Lambda_m(V)\).

Dann besitzt das äußere Produkt \(\wedge\) von antisymmetrischen Tensoren die folgenden Eigenschaften:

\((\omega \wedge \eta) \wedge \tau = \omega \wedge (\eta \wedge \tau), \qquad \) (Assoziativität)
\((\omega + \lambda \omega') \wedge \eta = \omega \wedge \eta + \lambda \omega' \wedge \eta\quad\) und analog im 2. Argument, (Bilinearität)
\(\omega \wedge \eta = (-1)^{kl} \eta \wedge \omega. \qquad\) (Antikommutativität)

Proof. In der Hausaufgabe zu zeigen.

Mit Hilfe der obigen Eigenschaften, insbesondere der Assoziativität, lässt sich das äußere Produkt für \(k \in \N\) Tensoren verallgemeinern, wie folgende Bemerkung festhält.

Remark 3.13 (\(k\)-faches äußeres Produkt)

Sei \(V\) ein endlich-dimensionaler, reeller Vektorraum und seien \(\omega_i \in \Lambda_{n_i}(V), i=1,\ldots,k\) antisymmetrische Vektoren der Stufe \(n_i \in \N\).

Dann gilt für das \(k\)-fache äußere Produkt von antisymmetrischen Tensoren,

(3.5)¶\[\omega_1 \wedge \ldots \wedge \omega_k = \frac{(n_1 + \ldots + n_k)!}{n_1!\cdot \ldots \cdot n_k!} \Pi_-(\omega_1 \otimes \ldots \otimes \omega_k).\]

Das folgende Theorem erweist sich als nützliche Einsicht, die im Laufe der Vorlesung noch von Bedeutung sein wird. Es besagt, dass das äußere Produkt von Linearformen mittels einer Determinante berechnet werden kann.

Theorem 3.3 (Äußeres Produkt von Linearformen)

Sei \(V\) ein endlich-dimensionaler, reeller Vektorraum und \(k \in \N\). Seien außerdem \(\omega_1, \ldots, \omega_k \in V^\ast\) Linearformen auf \(V\) und \(v_1, \ldots, v_k \in V\) beliebige Vektoren.

Dann lässt sich der antisymmetrische, rein kovariante Tensor \(k\)-ter Stufe, der durch das äußere Produkt \(\omega_1 \wedge \ldots \wedge \omega_k \in \Lambda_k(V)\) gegeben ist berechnen als

\[\begin{split}(\omega_1 \wedge \ldots \wedge \omega_k)(v_1, \ldots, v_k) = \operatorname{det} \begin{pmatrix} \omega_1(v_1) & \cdots & \omega_k(v_1)\\ \vdots & & \vdots \\ \omega_1(v_k) & \cdots & \omega_k(v_k) \end{pmatrix}.\end{split}\]

Proof. Seien \(v_1,\ldots,v_k \in V\) beliebige Vektoren. Dann gilt nach der Definition des \(k\)-fachen äußeren Produkts in (3.5) folgender Zusammenhang

\[\begin{split}(\omega_1 \wedge \ldots \wedge \omega_k)(v_1, \ldots, v_k) &= \frac{(1+\ldots+1)!}{1!\cdot\ldots\cdot1!} \cdot \Pi_-(\omega_1 \otimes \ldots \otimes \omega_k)(v_1,\ldots,v_k) \\ &= k! \cdot \Pi_-(\omega_1 \otimes \ldots \otimes \omega_k)(v_1,\ldots,v_k) \\ &= k! \frac{1}{k!} \sum_{\pi\in \mathcal{S}_k}\operatorname{sgn}(\pi) (\omega_1 \otimes \ldots \otimes \omega_k)(v_{\pi(1)},\ldots,v_{\pi(k)}) \\ &= \sum_{\pi\in \mathcal{S}_k}\operatorname{sgn}(\pi) \, \omega_1(v_{\pi(1)})\cdot \ldots \cdot \omega_k(v_{\pi(k)}) \\ &= \operatorname{det} \begin{pmatrix} \omega_1(v_1) & \cdots & \omega_k(v_1)\\ \vdots & & \vdots \\ \omega_1(v_k) & \cdots & \omega_k(v_k) \end{pmatrix}.\end{split}\]

Bei der letzten Gleichung haben wir den Determinantenproduktsatz aus Satz 3.40 in [Bur20] verwendet.

Das folgende Lemma weist auf eine interessante Eigenschaft des Vektorraums der antisymmetrischen Tensoren hin, für den Fall, dass die Stufe der zugehörigen Tensoren größer als die Dimension des zu Grunde liegenden Vektorraums \(V\) ist.

Lemma 3.10

Sei \(V\) ein endlich-dimensionaler, reeller Vektorraum mit \(\operatorname{dim}(V) = n \in \N\). Sei außerdem \(\Lambda_k(V)\) der Vektorraum der antisymmetrischen Tensoren der Stufe \(k\in\N\) mit \(k > n\). Dann gilt schon \(\Lambda_k(V) = \lbrace 0 \rbrace\).

Proof. Da \(V\) ein endlich-dimensionaler Vektorraum mit \(\operatorname{dim}(V)=n \in \N\) ist, wissen wir, dass eine Basis \(B\) von \(V\) aus \(n\) Vektoren \(B := \lbrace b_1,\ldots,b_n \rbrace \in V\) existiert. Dies bedeutet insbesondere, dass die Vektoren von \(B\) ein maximales System von linear unabhängigen Vektoren sind, die gleichzeitig noch ein Erzeugendensystem bilden. Jeder weitere Vektor \(v \in V\), den wir zu diesem System hinzunehmen lässt sich somit als Linearkombination der Basisvektoren von \(B\) darstellen.

Sei nun \(\omega \in \Lambda_k(V)\) ein antisymmetrischer, rein kovarianter Tensor der Stufe \(k > n\). Da dieser insbesondere eine \(k\)-Multilinearform darstellt, können wir für beliebige Vektoren \(v_1, \ldots, v_k \in V\) schreiben:

(3.6)¶\[\begin{split}\omega(v_1, \ldots, v_k) &= \omega(\sum_{i=1}^n \alpha_i^1 b_i, \ldots, \sum_{i=1}^n \alpha_i^k b_i) = \sum_{j_1=1}^n \alpha_{j_1}^1 \omega(b_{j_1}, \sum_{i=1}^n \alpha_i^2 b_i, \ldots, \sum_{i=1}^n \alpha_i^k b_i) \\ &= \sum_{j_1=1}^n \ldots \sum_{j_k=1}^n \alpha_{j_1}^1 \ldots \alpha_{j_k}^k \cdot \omega(b_{j_1}, \ldots, b_{j_k}).\end{split}\]

Wir sehen also, dass der Tensor sich auf die Wirkung der Basisvektoren von \(B\) zurückzuführen lässt und alle Summanden die Form \(\omega(b_{j_1}, \ldots, b_{j_k})\) besitzen. Da wir \(k > n\) angenommen haben, müssen mindestens zwei Basisvektoren gleich sein für jeden dieser Summanden.

Betrachten wir nun einen einzelnen Summanden für den wir ohne Beschränkung der Allgemeinheit annehmen, dass der der \(s\)-te und \(t\)-te Eintrag gleich sind für \(1 \leq s \neq t \leq n\), d.h., \(b_{j_s}=b_{j_t}\). Da der Tensor \(\omega\) antisymmetrisch ist, gilt jedoch:

\[\begin{split}\omega(b_{j_1}, \ldots, b_{j_s}, \ldots, b_{j_t}, \ldots, b_{j_k}) &= (-1) \cdot \omega(b_{j_1}, \ldots, b_{j_t}, \ldots, b_{j_s}, \ldots, b_{j_k}) \\ &= - \omega(b_{j_1}, \ldots, b_{j_s}, \ldots, b_{j_t}, \ldots, b_{j_k}) = 0.\end{split}\]

Da also jeder Summand in (3.6) Null ist, handelt es sich also bei dem antisymmetrischen Tensor \(\omega\) um den Nulltensor, der alle Tupel \((x_1, \ldots, x_k) \in V^k\) auf die Null abbildet. Hieraus folgt nun die Behauptung, denn es gilt \(\Lambda_k(V) = \lbrace 0 \rbrace\) für \(k > n =\operatorname{dim}(V)\).

Mit der Aussage aus Lemma 3.10 wird klar, dass wenn wir die direkte Summe der Vektorräume von antisymmetrischen Tensoren der Stufe \(k\) bilden, wir nur bis zur Stufe \(k = n = \operatorname{dim}(V)\) gehen müssen, da anschließend nur Nullvektorräume hinzugefügt werden. Das heißt insbesondere, dass für den \(\R\)-Vektorraum der durch die direkte Summe gebildet wird gilt:

\[\Lambda(V) := \bigoplus_{k=1}^\infty \Lambda_k(V) = \bigoplus_{k=1}^n \Lambda_k(V).\]

Mit dieser Erkenntnis lässt sich die sogenannte Grassmann-Algebra für antisymmetrische Tensoren definieren, wie folgende Bemerkung festhält.

Remark 3.14 (Grassmann-Algebra)

Die Menge

\[\Lambda(V) := \bigoplus_{k=1}^n \Lambda_k(V) = \Lambda_1(V) \times \ldots \times \Lambda_n(V)\]

bildet zusammen mit den Verknüpfungen der Tensoraddition „\(+\)“ und der skalaren Multiplikation „\(\cdot\)“ in \(\R\) als direkte äußere Summe von Vektorräumen wiederum einen reellen Vektorraum \((\Lambda(V), +, \cdot)\).

Erweitert man diesen um die bilineare Verknüpfung, die durch das äußere Produkt \(\wedge\) in Definition 3.10 beschrieben wird, so erhält man eine Algebra \((\Lambda(V), +, \cdot, \wedge)\). Diese wird auch Grassmann-Algebra oder äußere Algebra genannt.

Mathematik für Physikstudierende C

Tensoren und Tensorprodukte

Inhalt

3.2. Tensoren und Tensorprodukte¶

3.2.1. Motivation¶

3.2.2. Das Tensorprodukt¶

3.2.3. Existenz und Konstruktion des Tensorprodukts¶

3.2.4. Natürliche Homo- und Isomorphismen des Tensorprodukts¶

3.2.5. Tensoren als Multilinearformen¶

3.2.6. Symmetrie und Antisymmetrie von Tensoren¶

3.2.7. Grassmann-Algebra¶