5.1. Maßtheorie¶

Wir wollen in diesem Kapitel formal die Maßtheorie einführen, die es uns erlaubt zu entscheiden welche Mengen messbar sind und wie sich das Volumen von Mengen in topologischen Räumen bestimmen lässt. Die hier beschriebenen Werkzeuge werden uns im nächsten Kapitel bei der Einführung des Lebesgue-Integrals als Verallgemeinerung des Riemann-Integrals sehr dienlich sein.

Intuitiv ordnet ein Maß $\mu$, welches auf einer Menge $\Omega$ definiert ist, wie z.B. dem $\R^n$, allen geeigneten Teilmengen $A\subseteq \Omega$ nichtnegative reelle Zahlen zu, d.h.

\[\mu(A)\in[0,\infty] := [0,\infty)\cup\{\infty\}.\]

Hierbei soll das Maß $\mu$ natürlich mit dem Volumen der Teilmenge $A$ zusammenhängen. Man beachte, dass wir auch explizit unendliche Maße zulassen, z.B., falls die Menge $\Omega$ schon der gesamte $\R^n$ ist.

Bevor wir den Begriff des Maßes formal definieren können und dessen Eigenschaften näher diskutieren, müssen wir jedoch noch mehr Verständnis für die zu Grunde liegenden Mengen und Mengensystem entwickeln.

5.1.1. Mengensysteme¶

Wir betrachten im Folgenden eine beliebige zu Grundmenge $\Omega$, welche endlich, abzählbar oder auch überabzählbar sein kann. Ein Maß soll nun Teilmengen von $\Omega$ einen Wert zuordnen weshalb wir die Potenzmenge $2^\Omega$ betrachten, welche die Menge aller möglichen Teilmengen von $\Omega$ bildet. Ein Maß ist dann (unter zusätzlichen Voraussetzungen, siehe Definition 5.5) eine spezielle Abbildung $\mu:\Sigma\to[0,\infty]$, wobei $\Sigma\subset 2^\Omega$ ein Mengensystem ist, welches man auch System der $\mu$-messbaren Mengen nennt.

Bemerkung

Mengen von Mengen nennen wir häufig auch Mengensysteme.

Bei der Konstruktion eines Maßes gibt es zwei teilweise konkurrierende Wünsche:

Möglichst vielen Mengen soll ein Volumen zugeordnet werden können, d.h., $\Sigma$ soll groß sein.
Das Maß disjunkt vereinigter Mengen soll gleich der Summe der einzelnen Maße sein.

Der erste Wunsch würde darauf hindeuten die Potenzmenge $2^\Omega$ als System der messbaren Mengen zu betrachten. Allerdings gibt es viele Fälle (siehe Das äußere Maß ist kein Maß) in welchen diese Wahl den zweiten Wunsch unmöglich machen. Deshalb ist die Strategie meist ein möglichst großes Teilmengensystem zu finden, s.d. der zweite Wunsch erfüllbar ist. Man steht also vor dem Problem geeignete Klassen von Mengensystemen zu betrachten.

Beginnt man also Minimalanforderungen an das System zu stellen führt das zunächst auf den Begriff eines Mengenrings.

Definition 5.1 (Mengenring)

Ein Mengensystem $\mathcal{R} \subset 2^{\Omega}$ heißt Mengen-Ring (im maßtheoretischen Sinne) auf einer Menge $\Omega$, falls die folgenden Eigenschaften erfüllt sind:

$\emptyset \in \mathcal{R}$
$A,B \in \mathcal{R} \Rightarrow (A \setminus B) \in \mathcal{R}$
$A,B \in \mathcal{R} \Rightarrow (A \cup B) \in \mathcal{R}$

Ein Mengenring hat zusätzlich folgende Eigenschaften, wobei wir für zwei Mengen $A,B$ mit

\[A\triangle B := (A\setminus B)\cup (B\setminus A)\]

die symmetrische Differenz bezeichnen.

Lemma 5.1

Es sei $\mathcal{R}$ ein Mengenring, dann gilt

$A,B \in \mathcal{R} \Rightarrow (A \cap B) \in \mathcal{R}$
$A,B \in \mathcal{R} \Rightarrow (A \triangle B) \in \mathcal{R}$

Proof. Die zweite Eigenschaft folgt direkt per Definition. Die erste Eigenschaft gilt, da

\[A\cap B = A\setminus (A\setminus B).\]

Remark 5.1 (Der Begriff Ring)

Aus der Algebra kennt man die Definition, dass die Struktur $(F,+,\cdot)$ Ring heißt, falls

$(F,+)$ eine abelsche Gruppe ist,
$(F,\cdot)$ eine Halbgruppe ist,
die Distributivgesetze gelten.

Betrachten wir für einen Mengenring $\mathcal{R}$ die Struktur $(\mathcal{R}, \triangle, \cap)$ so fällt auf, dass $(\mathcal{R},\triangle)$ eine abelsche Gruppe mit Nullelement $\emptyset$ ist. Insbesondere gilt $A\triangle A=\emptyset$ und somit existieren auch inverse Elemente. Weiterhin sind Mengenschnitte assoziativ und daher ist $(\mathcal{R}, \cap)$ eine Halbgruppe. Somit bildet $(\mathcal{R},\triangle,\cap)$ einen Ring mit neutralem Element $\emptyset$, insbesondere ist er kommutativ.

Zwar erlaubt ein Mengenring die wichtigsten (endlichen) Mengenoperationen, es fällt aber schnell auf, dass die Grundmenge $\Omega$ nicht zwangsweise in einem Mengenring enthalten sein. In vielen Fällen will man dies aber sicherstellen, was auf folgenden Begriff führt.

Definition 5.2

Es sei $\mathcal{R}$ ein Mengenring über der Menge $\Omega$, gilt auch $\Omega\in\mathcal{R}$, dann nennen wir $\mathcal{R}$ Mengenalgebra.

Remark 5.2 (Der Begriff Algebra)

Eine Algebra über einem Körper $\K$ ist ein $\K$-Vektorraum $V$ zusammen mit einer bilinearen Abbildung

\[\begin{split}\cdot:V\times V&\to \V,\\ (x,y)&\mapsto x\cdot y.\end{split}\]

Man beachte, dass das Symbol $\cdot$ hier nun doppelt verwendet wird, einmal für die Skalarmultiplikation von $V$ über $\K$ und für die Multiplikation in $V$.

Eine Verallgemeinerung besteht hier darin keinen Vektorraum $V$ zu betrachten sondern ein $F$-Modul über einen kommutativen Ring $(F,+,\cdot)$. Hier erhält man nun, dass jeder kommutative Ring $F$ mit einem Einselement eine Algebra über sich selbst ist, wobei die bilineare Abbildung

\[\cdot:F\times F\to F\]

gerade durch das Produkt auf dem Ring $F$ gegeben ist.

Für den Mengenring $(\mathcal{R},\triangle, \cap)$ ist die Grundmenge $\Omega$ das neutrale Element der Multiplikation $\cap$ und daher gilt, falls $\Omega\in\mathcal{R}$, dass $(\mathcal{R},\triangle, \cap)$ ein kommutativer Ring mit Eins und daher eine Algebra über sich selbst ist.

Die bisher betrachteten System erlauben lediglich endliche Mengenoperationen. Wir benötigen im Folgenden aber auch abzählbare Mengenoperationen, und definieren daher sogenannte $\sigma$-Algebren.

Definition 5.3 ($\sigma$-Algebra und Messraum)

Ein Mengensystem $\Sigma \subseteq 2^\Omega$ heißt $\sigma$-Algebra (von $\Omega$), wenn die folgenden Eigenschaften erfüllt sind

$\Omega\in \Sigma$
$A\in \Sigma \quad \Rightarrow \quad A^c:=\Omega \setminus A\in \Sigma$
$(A_n)_{n\in\N} \in \Sigma \quad \Rightarrow \quad \bigcup_{n\in \N} A_n\in \Sigma$.

Für eine $\sigma$-Algebra $\Sigma \subseteq \mathcal{P}(\Omega)$ von $\Omega$ nennen wir das Paar ($\Omega,\Sigma$) Messraum und die Mengen des Mengensystems $\Sigma$ heißen messbar.

Das Symbol $\sigma$ erinnert an den Begriff der Summe, insbesondere wegen der dritten Eigenschaft in Definition 5.3, also der Abgeschlossenheit unter abzählbarer Vereinigung von Teilmengen. Aus diesen drei Eigenschaften lässt sich auch direkt zeigen, dass $\sigma$-Algebren ebenfalls unter abzählbaren Schnitten abgeschlossen sind, wie das folgende Lemma zeigt.

Lemma 5.2 (Abgeschlossenheit unter abzählbaren Schnitten)

Es sei ($\Omega,\Sigma$) ein Messraum und es sei $(A_i)_{i\in_\N}$ eine Familie von Elementen der $\sigma$-Algebra $\Sigma$ mit $A_i \in \Sigma$ für $i \in \N$. Dann sind abzählbare Schnitte dieser Mengen auch Elemente der $\sigma$-Algebra $\Sigma$, d.h.,

\[\bigcap_{n \in \N} A_n \in \Sigma.\]

Proof. Es reicht die Aussage für $n=2$ zu zeigen. Seien dazu $A_1,A_2\in\Sigma$, dann folgt $A_1^C,A_2^C\in\Sigma$ und somit auch $A^C\cup A_2^C\in\Sigma$. Und somit folgt

\[A_1\cap A_2 = (A_1^C\cup A_2^C)^C \in \Sigma.\]

Aus der Definition 5.3 kann man sich leicht zwei Spezialfälle von $\sigma$-Algebren überlegen. Es wird klar, dass das Mengensystem $\{\emptyset, \Omega\}$ die kleinstmögliche $\sigma$-Algebra bildet, wohingegen die Potenzmenge $\mathcal{P}(\Omega)$ die größtmögliche $\sigma$-Algebra darstellt.

Für ein beliebiges Mengensystem $\mathcal{C}\subset 2^\Omega$ können wir zusätzlich die erzeugt $\sigma$-Algebra betrachten, welche die kleinste $\sigma$-Algebra ist die $\mathcal{C}$ enthält.

Definition 5.4 (Erzeugte $\sigma$-Algebra)

Es sei $\mathcal{C}\subset 2^\Omega$ ein Mengensystem, dann bezeichnen wir mit

\[\begin{split}\sigma(\mathcal{C}) := \bigcap_{\substack{\Sigma \text{ ist $\sigma$-Algebra}\\ \mathcal{C} \subset \Sigma}} \Sigma\end{split}\]

die von $\mathcal{C}$ erzeugte $\sigma$-Algebra.

Für die erzeugt $\sigma$-Algebra, haben wir folgende Eigenschaften.

Lemma 5.3

Es sei $\mathcal{C}\subset 2^\Omega$ ein Mengensystem, dann gilt

$\sigma(\mathcal{C})$ ist eine $\sigma$-Algebra.
$\sigma(\mathcal{C})$ ist die kleinste $\sigma$-Algebra die $\mathcal{C}$ enthält, d.h., falls $\mathcal{C}\subset\Sigma$ eine weitere $\sigma$-Algebra ist, so folgt $\sigma(\mathcal{C})\subset\Sigma$.
Falls $\mathcal{C}$ selbst eine $\sigma$-Algebra ist, so folgt $\sigma(\mathcal{C}) = \mathcal{C}$.

Proof. Übung.

5.1.2. Maße¶

Basierend auf dem Begriff einer $\sigma$-Algebra und eines Messraums können wir nun formal einführen, was wir unter einem Maß verstehen.

Definition 5.5 (Maß und Maßraum)

Sei $(\Omega, \Sigma)$ ein Messraum. Wir nennen eine Abbildung $\mu: \Sigma\to [0, \infty]$ Maß, wenn die folgenden beiden Eigenschaften erfüllt sind.

Die leere Menge hat das Maß Null, d.h., $\mu(\emptyset) = 0$,
Für eine Familie von disjunkten Mengen $(A_n)_{n\in\N}$ der $\sigma$-Algebra $\Sigma$ mit $A_i \cap A_j = \emptyset$ für $i \neq j$ gilt die sogenannte abzählbare oder $\sigma$-Additivität, d.h.,

\[\mu\left( \bigcup_{n\in\N}A_n \right) = \sum_{n\in\N}\mu (A_n).\]

Wir nennen das Maß $\mu$ endlich, wenn $\mu(\Omega)<\infty$. Das Tripel $(\Omega, \Sigma, \mu)$ wird als Maßraum bezeichnet.

Remark 5.3

Maße spielen insbesondere in der Wahrscheinlichkeitstheorie eine zentrale Rolle, um die Wahrscheinlichkeit von Ereignismengen anzugeben. Dabei wird nicht nur gefordert, dass das Maß $\mu$ endlich sein muss, sondern dass sogar $\mu(\Omega)=1$ gilt, damit es sich um ein Wahrscheinlichkeitsmaß handelt. Diese finden vor allem in der Quantenmechanik Anwendung.

Aus den beiden grundlegenden Eigenschaften eines Maßes lassen sich weitere nützliche Eigenschaften herleiten, wie das folgende Lemma beschreibt.

Lemma 5.4 (Eigenschaften von Maßen)

Sei $(\Omega, \Sigma, \mu)$ ein Maßraum. Dann gelten die folgenden Eigenschaften für das Maß $\mu \colon \Sigma \rightarrow [0,\infty]$.

1. Für $A,B \in \Sigma$ mit $B \subset A$ und $\mu(B) < \infty$ gilt:

\[\mu(A \setminus B) = \mu(A) - \mu(B) \qquad \text{(Subtraktivität)}\]

2. Für $A,B \in \Sigma$ mit $B \subset A$ gilt:

\[\mu(B) \leq \mu(A) \qquad \text{(Monotonie)}\]

3. Für $A,B \in \Sigma$ gilt stets:

\[\mu(A \cup B) = \mu(A) + \mu(B) - \mu(A \cap B).\]

Proof. In der Hausaufgabe zu zeigen.

Im Folgenden wollen wir ein paar Beispiele von geläufigen Maßen diskutieren.

Example 5.2 (Maße)

Wichtige Maße in der Mathematik und Physik sind beispielsweise die folgenden.

1. Das Zählmaß $m$ auf einer endlichen Menge $M$, mit

\[m(A):=|A|\qquad (A\subseteq M).\]

Hier sind insbesondere alle Teilmengen messbar, d.h., $(M, \mathcal{P}(M), m)$ bildet einen Maßraum.

2. Das Lebesgue–Maß $\lambda^n$ auf dem $\R^n$, das wir bald kennen lernen, zeichnet sich dadurch aus, dass es einer verschobenen Menge das gleiche Volumen zuordnet wie einer unverschobenen. Es besitzt also die nützliche Eigenschaft translations- und rotationsinvariant zu sein. Dies gilt ebenfalls für Spiegelungen. Außerdem ordnet das Lebesgue-Maß dem Einheitswürfel $[0,1]^n$ das Maß $1$ zu, was unserer Intuition entspricht. Andererseits stellt sich heraus, dass das Lebesgue-Maß nicht auf der gesamten Potenzmenge $\mathcal{P}(\R^n)$ definiert werden kann.

3. Das Dirac-Maß $\delta_x$ ist im Punkt $x \in \R^n$ konzentriert, und für jede Teilmenge $A\subset\R^n$ gilt

\[\begin{split}\delta_x(A) \equiv \int_A\delta_x := \begin{cases} 1, & \text{ falls } x \in A,\\ 0, & \text{ sonst}. \end{cases}\end{split}\]

Dieses Maß ist im Gegensatz zum Lebesgue-Maß nicht translationsinvariant, da es explizit von der Lage des Punkts $x\in\R^n$ abhängt. Es wird beispielsweise in der Elektrodynamik benutzt, um eine in $x$ lokalisierte, punktförmige Ladung zu beschreiben.

4. Häufig möchte man die Länge einer Kurve oder allgemeiner den Flächeninhalt einer $d$-dimensionalen Fläche im $\R^n$ messen. Auch das dafür benutzte Maß $\mu_d$ ist translations- und rotationsinvariant, es ordnet aber der $d$-dimensionalen Einheitsfläche $[0,1]^d\times\{0\} \subset\R^d\times\R^{n-d}=\R^n$ das Maß $1$ zu. Entsprechend hat aber für $d<n$ der Einheitswürfel das Maß $\mu_d([0,1]^n)=\infty$.

5. Man kann sogar sogenannte Hausdorff-Maße $\mu_d$ konstruieren, die Mengen beliebiger fraktaler Dimension $d\in[0,n]$ messen. Genau genommen definiert man hierbei die Dimension der Menge $A\subset \R^n$ durch $d(A):=\inf\{d'>0\mid \mu_{d'}(A)=0\}.$

6. Im Zusammenhang mit dem sogenannten Feynmanschen Pfadintegral der Quantenmechanik wird auf dem unendlich-dimensionalen Raum $\Omega$ der Weg zwischen zwei Punkten des Konfigurationsraumes $\R^d$ ein Wahrscheinlichkeitsmaß (siehe Remark 5.3) definiert. Dabei erhalten Pfade, die in der Nähe von Lösungskurven der DGL der Klassischen Mechanik sind, ein größeres Gewicht als beliebige Pfade.

Eine sehr nützliche Eigenschaft von gewissen Maßen auf topologischen Räumen ist die der Regularität, welche wir im Folgenden definieren wollen.

Definition 5.6 (Regularität von Maßen)

Es sei $(\Omega, \tau)$ ein topologischer Raum und $(\Omega, \Sigma, \mu)$ ein entsprechender Maßraum auf $\Omega$, so dass gilt $\tau \subset \Sigma$. Dann können wir die Regulariät des Maßes $\mu$ wie folgt definieren.

Wir nennen das Maß $\mu$ von außen regulär, wenn zu jeder messbaren Menge $A \in \Sigma$ und jedem $\epsilon > 0$ eine offene Obermenge $U \in \tau$ existiert mit $A \subset U$, so dass für das Maß $\mu(U\setminus A) < \epsilon$ gilt.
Wir nennen das Maß $\mu$ von innen regulär, wenn zu jeder messbaren Menge $A \in \Sigma$ und jedem $\epsilon > 0$ eine abgeschlossene Teilmenge $F \subset A$ gibt, so dass für das Maß $\mu(A\setminus F) < \epsilon$ gilt.

5.1.3. Borel-Maße¶

Neben $\sigma$-Algebren kennen wir auch Topologien als wichtige Klasse von Mengensystemen, da diese es z.B. erlauben Stetigkeit von Funktionen zu definieren. Wir betrachten nun ein Konzept welches den Begriff einer Topologie mit der einer $\sigma$-Algebra vereint, die sogenannte Borel-$\sigma$-Algebra.

Definition 5.7 (Borel-$\sigma$-Algebra)

Die Borel-$\sigma$-Algebra auf einem topologischen Raum $(\Omega, \tau)$ ist die von $\tau$ erzeugte $\sigma$-Algebra,

\[\B(\Omega) := \sigma(\tau).\]

Remark 5.4 (Borelsche $\sigma$-Algebra von $\R$)

Wir bemerken, dass die Borelsche $\sigma$-Algebra von $\R$ nicht alle Teilmengen von $\R$ enthält. Es lässt sich sogar zeigen, dass die borelsche $\sigma$-Algebra von $\R$ gleichmächtig zu $\R$ ist, während die Potenzmenge $2^\R$ eine echt größere Mächtigkeit als $\R$ besitzt.

Man erkennt an der Notaion, dass die Topologie $\tau$ meist unterschlagen wird. Man spricht meist auch vom topologischen Raum $\Omega$ ohne $\tau$ zu nennen. Ein Maß auf dieser $\sigma$-Algebra nennen wir auch Borel-Maß.

Definition 5.8

Es sei $\Omega$ ein topologischer Raum, dann heißt ein Maß $\mu$ auf $\B(\Omega)$ Borel-Maß.

5.1.3.1. Erzeugte Topologien¶

Das Konzept der erzeugten $\sigma$-Algebra lässt sich auch auf Topologien übertragen. Hierbei betrachtet man meist eine sogenannte Basis einer Topologie.

Definition 5.9

Es sei $(\Omega,\tau)$ ein topologischer Raum, ein System $\mathcal{C}\subset 2^\Omega$ heißt Basis für $\tau$, falls für jede Menge $U\in\tau$ Teilmengen aus $\mathcal{C}$ existieren, $J\subset\mathcal{C}$, s.d.,

\[\bigcup_{A\in J} A = U.\]

In diesem Fall schreiben wir auch $\tau(\mathcal{C})=\tau$.

Besonders relevant sind für uns die Mengensysteme, welche die kanonische Topologie für $\R$ erzeugt. Hierbei wissen wir, dass alle offene Intervalle der Form $(a,b)\subset \R$, sowie alle Intervalle der Form $(-\infty, b)$ und $(a, \infty)$ die euklidische Topologie in $\R$ erzeugen. Wir betrachten weiterhin ein derartiges Mengenssystem bestehend aus Intervallen, welche die Borel-$\sigma$-Algebra erzeugt.

Lemma 5.5

Es sei

\[\mathcal{C} = \{ [-\infty, c):c\in\R\}\]

dann gilt $\sigma(\mathcal{C}) = \B(\overline{\R})$.

5.1.3.2. Eigenschaften von Borel-Maßen¶

Für spezielle topologische Räume lässt sich eine wichtige Eigenschaft von Maßen über die Borel-$\sigma$-Algebra definieren.

Definition 5.10 (Lokale Endlichkeit von Maßen)

Sei $(\Omega, \tau)$ ein Haussdorf-Raum (siehe Definition 4.8) und sei $\B(\Omega) = \sigma(\tau)$ die Borel-$\sigma$-Algebra, die durch $\tau$ erzeugt wird. Wir nennen ein Maß $\sigma \colon \B(\Omega) \rightarrow [0, \infty]$ lokal endlich, falls jeder Punkt $x \in \Omega$ eine lokale Umgebung mit endlichem Maß besitzt.

Die lokale Endlichkeit ist essentiell bei der Untersuchung von Maßen auf topologischen Räumen, weil sie für jeden Punkt die Existenz einer Umgebung mit endlichem Maß garantiert. Wie wir später sehen werden ist das Lebesgue-Maß auf dem Raum $\R^n$ lokal endlich.

Basierend auf der oben definierten Borel-$\sigma$-Algebra lässt sich nun das sogenannte Borel-Maß einführen.

Definition 5.11 (Borel-Maß)

Ein lokal endliches Maß $\sigma \colon \B(\Omega) \rightarrow [0, \infty]$ auf der Borelschen $\sigma$-Algebra eines Hausdorff-Raums $(\Omega,\tau)$ heißt Borel-Maß.

5.1.4. Das Lebesgue Maß¶

Bei der Einführung des Riemann Integrals verwendet man Intervalle zur Unterteilung des Definitionsbereichs. Diese Partitionierung einer Menge lässt sich im $\R^n$ auf mehrdimensionale Quader verallgemeinern. Für $a = (a_1,\ldots,a_n) \in \R^n$ und $b = (b_1,\ldots,b_n) \in \R^n$ verwenden wir hierbei die Anordnungsrelation

\[a < b \qquad \Leftrightarrow \qquad a_i < b_i \quad i=1,\ldots,n\]

und analog für $a \leq b, a > b$ und $a \geq b$.

Definition 5.12 (Mehrdimensionale Quader)

und darüber im Folgenden offene, halboffene und abgeschlossene Quader im $\R^n$ respektive beschreiben durch

\[\begin{split}(a,b) &= \lbrace x \in \R^n : a < x < b \rbrace,\\ (a,b] &= \lbrace x \in \R^n : a < x \leq b \rbrace,\\ [a,b] &= \lbrace x \in \R^n : a \leq x \leq b \rbrace.\end{split}\]

Das Volumen bzw. der Lebesgue-Inhalt eines halboffenen Quaders $Q := (a,b] \subset \R^n$ definieren wir über

\[\lambda^n(Q) := \prod_{i=1}^n (b_i - a_i).\]

Wir wollen im Folgenden das Teilmengensystem $\mathcal{R}_{\text{Q}}\subset\ 2^{\R^n}$ aller halboffenen Quader betrachten,

\[\mathcal{R}_{\text{Q}} := \left\{ \bigsqcup_{i=1,\ldots,k} Q_i \colon Q_i \text{ ist halboffener Quader im } \R^n \right\}.\]

Wir fordern hierbei nicht, dass nur disjunkte Quader vereinigt werden dürfen. Jedoch kann man direkt herleiten, dass man jede Vereinigung von Quadern in eine disjunkte Umschreiben kann. Seien dazu $Q_1,\ldots,Q_k\subset\R^n$ halboffene Quader, wir erkennen, dass der Rand eines Quaders $Q_i=(a^i,b^i]$ genau $2n$ Hyperebenen der Form

\[\begin{split}x_j = a^i_j\\ x_j = b^i_j\end{split}\]

für $j=1,\ldots,n$ aufspannt. Weiterhin, können wir einen anderen Quader $Q_m=(a^k,b^k)$ mit einer Hyperebene $x_l=c\in\R$ zerteilen, im Falle $a^k_l < c < b^k_l$, indem wir zwei neue Quader definieren mit

\[\begin{split}\alpha^m&:=(a^m_1,\ldots,c,\ldots,a^m_n)\\ \beta^m&:=(b^m_1,\ldots,c,\ldots,b^m_n)\\ Q_m^1&=(a^m,\beta^m]\\ Q_m^2&=(\alpha^m,b^m].\end{split}\]

Iterativ gehen wir folgendermaßen vor:

Betrachte den ersten Quader $Q_1$, zerteile alle Quader $Q_i$ an allen seinen Hyperebenen und erhalte so neue Quader $W^1_j$.
Im $i+1$ten Schritt betrachte die Hyperebenen des Quaders $Q_{i+1}$ und zerteile damit alle Quader $W^i_j$ aus dem vorherigen Schritt und erhalte damit neue Quader $W^{i+1}_j$.

Führen wir diesen Prozess bis $i=k$ durch, so erhalten wir folgendes Resultat, welches in Abb. 5.2 visualisiert ist.

Abb. 5.2 Nicht disjunkte Quader werden in System disjunkter Quader überführt. Man erkennt insbesondere, dass die Vereinigung gleich bleibt und, dass sich jeder einzelne ursprüngliche Quader, aus den neuen Quadern zusammensetzbar ist.¶

Lemma 5.6

Es seien $Q_1,\ldots,Q_k\subset\R^d$ halboffene Quader, dann existieren paarweise disjunkte halboffene Quader $W_1,\ldots, W_M$ mit Indexmengen $J_i\subset\{1,\ldots,M\}$, s.d.

\[\bigcup_{i=1}^k Q_i = \bigcup_{j=^1}^M W_j\]

und für jedes $i\in\{1,\ldots,n\}$ gilt

\[\bigcup_{j\in J_i} W_j = Q_i.\]

Das System der halboffenen Quadern bildet eine besondere mathematische Struktur, einen Mengen-Ring.

Lemma 5.7 (Der von halboffenen Quadern erzeugte Ring)

Das System der halboffenen Quadern $\mathcal{R}_{\text{Q}}$ bildet einen Mengenring.

Proof. Um zu zeigen, dass es sich bei dem Mengensystem $\mathcal{R}_{\text{Q}}$ um einen Ring handelt müssen wir die Eigenschaften aus Definition 5.1 nachweisen.

1. Für einen beliebigen Punkt $a \in \R^n$ gilt $\emptyset = (a,a] \in \mathcal{R}_{\text{Q}}$.

2. Als nächstes müssen wir zeigen, dass für zwei Mengen $A,B \in \mathcal{R}_{\text{Q}}$ gilt, dass auch die Mengendifferenz in $\mathcal{R}_{\text{Q}}$ enthalten ist, d.h., dass gilt $(A \setminus B) \in \mathcal{R}_{\text{Q}}$. Nach {prf:ref}``disRect` existieren paarweise disjunkte halboffene Quader $S_j$, $j=1,\ldots,n$, und Indexmengen $I_A,I_B\subset\{1,\ldots,n\}$, s.d.,

\[\begin{split}A = \bigcup_{j\in I_A} S_j\\ B = \bigcup_{j\in I_B} S_j.\end{split}\]

Somit gilt dann

\[\begin{split}A\setminus B &= \left(\bigcup_{j\in I_A} S_j\right) \setminus \left(\bigcup_{j\in I_B} S_j\right)\\ &= \bigcup_{j\in I_A\setminus I_B} S_j\end{split}\]

was wieder eine Vereinigung von halboffenen Quadern ist und deshalb gilt $A\setminus B\in \mathcal{R}_{\text{Q}}$.

3. Zuletzt erkennen wir für zwei Mengen $A,B \in \mathcal{R}_{\text{Q}}$, dass mit der Zerlegung aus 2. gilt

\[A\cup B = \bigcup_{j=1}^n S_j\]

und somit ist auch $A\cup B\in\mathcal{R}_{\text{Q}}$ als Vereinigung halboffener Quader.

Damit haben wir gezeigt, dass das Mengensystem $\mathcal{R}_{\text{Q}}$, welches durch disjunkte halboffene Quader im $\R^n$ erzeugt wird, einen Ring bildet.

Wir können den Lebesgue-Inhalt nun auf Elemente von $\mathcal{R}_{\text{Q}}$ fortsetzen

Definition 5.13

Es sei $A\in\mathcal{R}_{\text{Q}}$ mit $A=\bigcup_{i=1}^n Q_i$ wobei $Q_1,\ldots,Q_n$ paarweise disjunkte halboffene Quader sind, dann setzen wir

\[\lambda^n(A):=\sum_{i=1}^{n} \lambda^n(Q_i).\]

Remark 5.5

Man erkennt leicht, dass der Wert $\lambda^n(A)$ nicht von der Wahl der Zerlegung $Q_1,\ldots,Q_n$ abhängt, der Lebesgue-Inhalt ist also wohldefiniert.

Für den Lebesgue-Inhalt auf $\mathcal{R}$ können wir folgende Eigenschaften zeigen.

Theorem 5.1

Der Lebesgue-Inhalt $\lambda^n$ auf $\mathcal{R}$ hat folgende Eigenschaften:

1. $\lambda^n(\emptyset) = 0$

2. Seien $A_1, \ldots, A_k \in \mathcal{R}$ disjunkte Mengen. Dann gilt:

\[\lambda^n \left( \bigcup_{i=1,\ldots,k} A_i \right) = \sum_{i=1}^k \lambda^n(A_i) \qquad (\text{endliche Additivität})\]

3. Für zwei Mengen $A, B \in \mathcal{R}$ mit $A \subset B$ gilt:

\[\lambda^n(A) \leq \lambda^n(B) \qquad (\text{Monotonie}).\]

4. Für zwei Mengen $A, B \in \mathcal{R}$ gilt:

\[\lambda^n(A \cup B) + \lambda^n(A \cap B) = \lambda^n(A) + \lambda^n(B).\]

5. Für beliebige Mengen $A_1, \ldots, A_k \in \mathcal{R}$ gilt:

\[\lambda^n\left( \bigcup_{i=1,\ldots,k} A_i\right) \leq \sum_{i=1}^k \lambda^n(A_i) \qquad (\text{endliche Subadditivität}).\]

6. Sei $(A_n)_{k\in\N}$ eine Folge von disjunkten Mengen in $\mathcal{R}$ und sei $B \in \mathcal{R}$, so dass $\bigcup_{k=1}^\infty A_k \subset B$, dann gilt

\[\sum_{k=1}^\infty \lambda^n(A_k) \leq \mu(B).\]

Proof. Ad 1.

Für $a\in\R^d$ haben wir

\[\lambda^n(\emptyset) = \lambda^n((a,a]) = \Pi_{i=1}^n (a_i - a_i) = 0.\]

Ad 2.

Für disjunkte Mengen $A_1,\ldots, A_k\in\mathcal{R}$ wählen wir für jedes $i\in\{1,\ldots,k\}$ paarweise disjunkte Quader $Q^i_1,\ldots, Q^i_{n_i}$, welche nach Lemma 5.6 existieren, s.d.,

\[A_i = \bigcup_{j=1}^{n_i} Q^i_j.\]

Da die $A_i$ paarweise disjunkt sind, gilt insbesondere

\[Q^i_j \cap Q^r_s = \emptyset\]

für $(i,j)\neq (r,s)$. Somit haben wir

\[\begin{split}\lambda^n\left(\bigcup_{i=1}^k A_i \right) &= \lambda^n\left(\bigcup_{i=1}^k \bigcup_{j=1}^{n_i} Q^i_j \right) \\&= \sum_{i=1}^k \sum_{j=1}^{n_i} \lambda^n(Q^i_j) \\&= \sum_{i=1}^k \lambda^n(A_i).\end{split}\]

Ad 3.

Es sei $A\subset B$, dann können wir $B$ disjunkt zerlegen mit

\[B = A \cup B\setminus A\]

und sehen dann unter Ausnutzung von 2.

\[\lambda^n(B) = \lambda^n((A\cap B)\cup B\setminus B) \overset{2.}{=} \lambda^n(A) + \underbrace{\lambda(B\setminus A)}_{\geq 0} \geq \lambda^n(A).\]

Ad 4.

Für zwei Mengen $A,B\in\mathcal{R}_{\text{Q}}$ sehen wir, dass

\[A\cup B = A \cup (B\setminus A),\]

gilt, wobei die Mengen auf der rechten Seite paarweise disjunkt sind. Mit 2. haben wir dann

\[\begin{split}\lambda^n(A\cup B) + \lambda^n(A\cap B) &= \lambda^n(A) + \lambda^n(B\setminus A) + \lambda^n(A\cap B) \\&= \lambda^n(A) + \lambda^n(B).\end{split}\]

Ad 5.

Nach 4. gilt für zwei Mengen $A,B\in\mathcal{R}$,

\[\lambda^n(A\cup B) = \lambda^n(A) + \lambda^n(B) - \lambda^n(A\cap B) \leq \lambda^n(A) + \lambda^n(B).\]

Diese Eigenschaft lässt sich direkt auf endliche viele Mengen $A_1,\ldots,A_k\in\mathcal{R}$ übertragen.

Ad 6.

Es sei $(A_i)_{i\in\N}\subset \mathcal{R}_{\text{Q}}$ eine Folge paarweiser disjunkter Mengen, s.d.,

\[\bigcup_{i\in\N} A_i\subset B\in \mathcal{R}_{\text{Q}}.\]

Dann gilt für $N\in\N$

\[\sum_{i=1}^N \lambda^n(A_i) \overset{2.}{=} \lambda^n\left(\bigcup_{i=1}^N\right) \overset{3.}{\leq} \lambda^n\left(\bigcup_{i=1}^\infty\right) \overset{3.}{\leq} \lambda^n(B).\]

Somit gilt mit $N\to\infty$

\[\sum_{i=1}^\infty \lambda^n(A_i) \leq \lambda^n(B).\]

5.1.4.1. Der Jordan-Inhalt und Jordan-messbare Mengen¶

Wir haben bisher einen Inhalt auf $\mathcal{R}_{\text{R}}$ definiert. Diese Klasse an Mengen ist aber relativ klein, weshalb der Begriff ausgedehnt werden soll. Eine Möglichkeit hier ist die Idee des Riemann-Integrals mit Ober- und Untersummen zu benutzen. Es stellt aber auch hier heraus, dass der Begriff zu einschränkend ist. Insbesondere führt deses Konzept nicht auf ein Maß. Wir werden es im Folgenden trotzdem betrachten.

Definition 5.14 (Jordan-messbare Mengen)

Sei $A \subset \R^n$ eine beliebige Teilmenge. Wir betrachten die folgenden endlichen Ober- und Untersummen für die Teilmenge $A$,

\[\begin{split}\iota^\ast(A) &:= \inf \left\{ \lambda^n(O) \, : A \subset O \in\mathcal{R}_{\text{R}}\right\},\\ \iota_\ast(A) &:= \sup \left\{ \lambda^n(U \, : A \supset U\in\mathcal{R}_{\text{R}} \right\}.\end{split}\]

Wir nennen die Teilmenge $A \subset \R^n$ Jordan-messbar, genau dann wenn $A$ beschränkt ist und die Ober- und Untersumme übereinstimmen, d.h., es gilt $\iota^\ast(A) = \iota_\ast(A)$. Für Jordan-messbare Mengen $A$ ist dann der Jordan-Inhalt $\iota$ gegeben durch:

\[\iota(A) = \iota^\ast(A) = \iota_\ast(A).\]

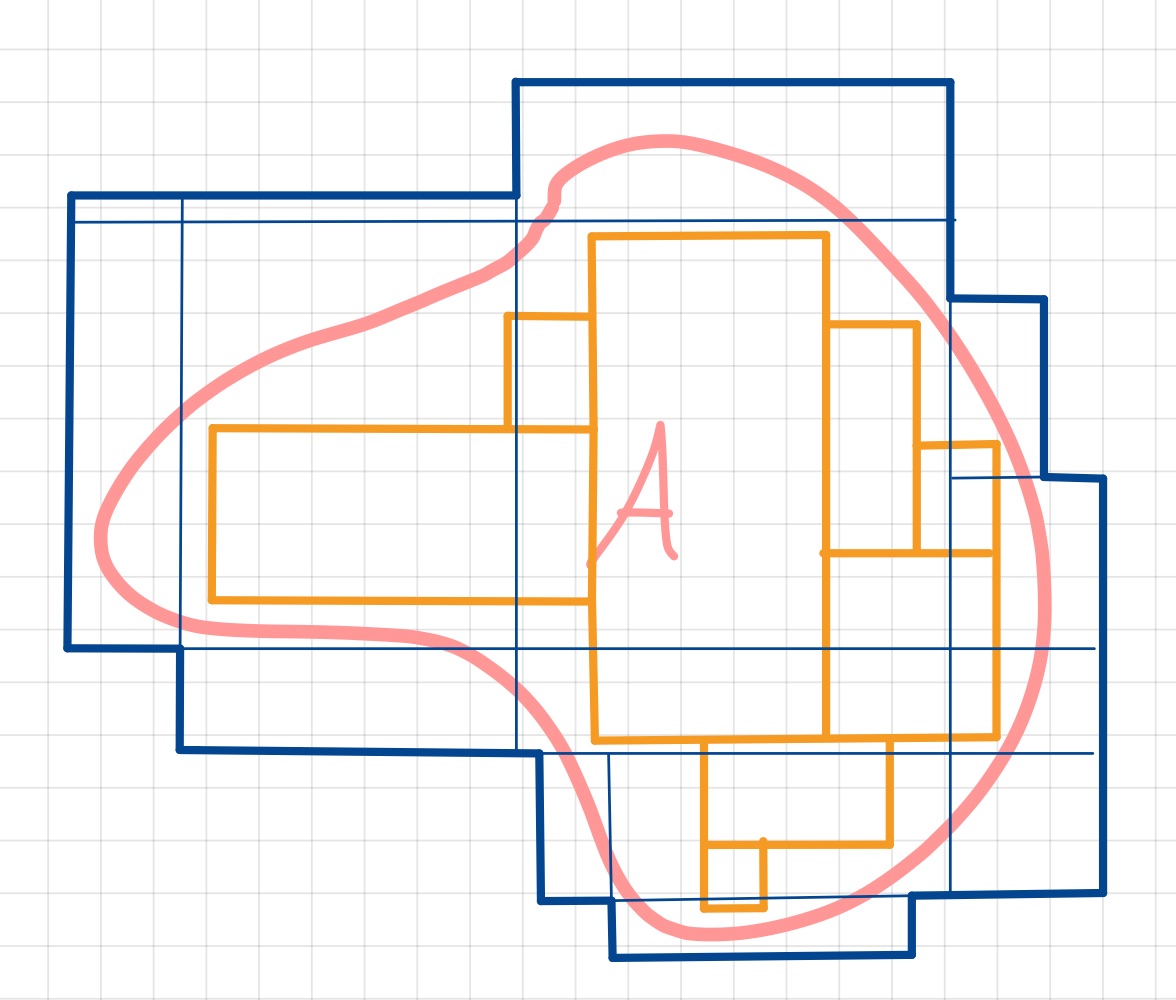
Abb. 5.3 Visualisierung einer Approximation für das äußere (blau) und das inner (orange) Maß.¶

Die Klasse der Jordan-messbaren Mengen ist erneut recht klein. Insbesondere hat dieses Konzept erneut Schwierigkeiten mit abzählbar unendlich großen Mengen umzugehen wie folgendes Beispiel zeigt.

Example 5.3

Wir betrachten die Menge

\[A = (0,1]\cap \mathbb{Q}\]

der rationalen Zahlen im Intervall $[0,1]$. Wir betrachten zunächst das äußere Maß und dazu eine Menge

\[J = \bigcup_{i=1}^N Q_i \supset A,\]

mit halboffenen Quader $Q_1,\ldots,Q_N$. Da aber $J$ und $(0,1]$ jeweils Elemente aus $\mathcal{R}_{\text{Q}}$ sind gilt auch $L = (0,1]\setminus J \in\mathcal{R}$. Wäre nun $L$ nicht leer, so gäbe es per Definition der halboffenen Quader eine offene Umgebung

\[U\subset L.\]

Da aber $A$ dicht in $(0,1]$ liegt und somit auch $J$ führt dies auf einen Widerspruch. Deshalb folgt $L=\emptyset$ und daher

\[(0,1]\subset J \Rightarrow 1\leq \iota^\ast(A).\]

Für das innere Maß betrachten wir

\[J = \bigcup_{i=1}^N Q_i \subset A,\]

angenommen $J$ wäre nicht leer, dann folgt dass eine offenen Umgebung $U$ existiert s.d.

\[U\subset J.\]

Da aber auch die irrationalen Zahlen $\R\setminus \mathbb{Q}$ dicht in $\R$ liegen folgt daher

\[\left[U\cap\R\setminus \mathbb{Q} \neq \emptyset\right] \Rightarrow \left[J \cap \R\setminus \mathbb{Q} \neq \emptyset\right] \Rightarrow \left[J\not\subset \mathbb{Q}\right]\]

was im Widerspruch zu $J\subset A$ steht, daher gilt

\[J=\emptyset\Rightarrow \iota_\ast(J) = 0\]

und somit

\[\iota_\ast(J) \neq \iota^\ast(J).\]

Die Menge der Jordan-messbaren Mengen bildet weiterhin keine $\sigma$-Algebra und daher ist der Jordan-Inhalt kein Maß im Sinne von Definition 5.5. Dies ist an folgendem Beispiel ersichtlich.

Example 5.4

Wir wollen den Jordan-Inhalt einer Punktmengen $\{a\}$ für $a\in\R$ berechnen. Mit der Argumentation aus Example 5.3 erkennen wir, dass das innere Maß gleich null ist, also

\[\iota_\ast(\{a\}) = 0.\]

Für das äußere Maß wählen wir eine Folge von offenen Quadern $Q_i:= (a-1/i, a] \supset \{a\}$ und erkennen, dass

\[\iota^\ast(\{a\})\leq \lim_{i\to\infty} \lambda^n(Q_i) = \lim_{i\to\infty} 1/i = 0\]

und damit ist jede Punktmenge Jordan-messbar.

Da aber $\mathbb{Q}$ abzählbar ist, können wir eine Folge $(q_i)_{i\in\N}$ finden, s.d.

\[A = (0,1]\cap \mathbb{Q} = \bigcup_{i\in\N} \{q_i\},\]

die Menge $A$ lässt sich also als abzählbare Vereinigung von Jordan-messbaren Mengen darstellen. Aus Example 5.3 wissen wir aber, dass $A$ nicht Jordan-messbar ist und somit bildet die Klassen der Jordan-messbaren Menge keine $\sigma$-Algebra.

5.1.4.2. Das äußere Lebesgue-Maß¶

Wir der letzte Abschnitt zeigt ist der Begriff der Jordan-messbarkeit einerseits zu einschränkend (siehe Example 5.3) und andererseits führt er nicht auf eine $\sigma$-Algebra. Wir werden diesen Begriff nun erweitern indem wir uns zunächst nur auf den äußeren Inhalt konzentrieren.

Bemerkung

Der innere und äußere Inhalt sind intuitiv nicht gleichberechtigt, da das Problem asymmetrisch ist. Konkret ist Subadditivität die inhärente Eigenschaft eines Maßes, da Mengenvereinigungen mehrfach auftretenden Elemente nicht berücksichtigen, während die Addition in $\R$ für positive Zahlen stets ein größeres Ergebnis liefert. Das äußere Maß ist auf natürliche Weise subadditiv und deshalb zu bevorzugen.

Definition 5.15 (Äußeres Lebesgue-Maß)

Das äußere Lebesgue-Maß $\lambda^* \colon 2^{\R^n} \rightarrow [0,\infty]$ ist definiert durch

\[\lambda^*(A) = \inf \left\{ \sum_{k=1}^\infty \mu^n(Q_k) : Q_k \text{ sind halboffene Quader mit } A \subset \bigcup_{k=1}^\infty Q_k \right\}.\]

Im Vergleich zum Jordan-Inhalt lassen wir nun also unendliche Vereinigungen zu und werten dann Reihen aus über welche das Infimum gebildet wird. Die erste wichtige Aussage in diesem Kontext geht auf Lebesgue zurück. Der Beweis des Satzes benutzt den Satz von Heine-Borel.

Theorem 5.2 (Heine-Borel)

Für eine Menge $\Omega\subset\R^n$ sind die folgenden beiden Aussagen äquivalent:

$\Omega$ ist beschränkt und abgeschlossen.
Jede offene Überdeckung von $\Omega$ enthält eine endliche Teilüberdeckung.

Proof. Siehe z.B. [For17].

Mit diesem Resultat können wir die folgende Aussage beweisen.

Theorem 5.3

Es sei $J\in\mathcal{R}_{\text{Q}}$ und $(Q_k)_{k\in\N}$ Folge halboffene Quader mit $J \subset \bigcup_{k=1}^\infty Q_k$. Dann gilt

\[\lambda^n(J) = \iota(J) = \leq \sum_{k=1}^\infty \lambda^n(Q_k).\]

Proof. Wir zeigen die Aussage zunächst für $J=Q$ wobei $Q$ ein halboffener Quader ist.

Idee: Verkleinere $Q$ und vergrößere die $Q_i$ um Heine-Borel anwenden zu können.

Es sei $\varepsilon>0$ gegeben. Für $Q=(a,b]$ können wir einen kleineren halboffenen Quader $Q_\varepsilon$ wählen, s.d.

\[\begin{split}\overline{Q_\varepsilon} \subset Q\\ \lambda^n(Q_\varepsilon) > \lambda^n(Q) - \varepsilon.\end{split}\]

Beachte, dass der Quader so gewählt wird, dass auch sein Abschluss noch in $Q$ enthalten ist, die zweite Bedingung gibt eine unter Schranke an wie klein der Quader gewählt werden darf. Man kann leicht nachrechnen, dass ein solcher Quader existiert.

Weiterhin wählen wir für jeden Quader $Q_k$ einen größeren Quader $Q_k^\varepsilon$, s.d.,

\[\begin{split}\text{Int}(Q_k^\varepsilon)\supset Q_k\\ \lambda^n(Q_k^\varepsilon) < \lambda^n(Q_k) + \frac{\varepsilon}{2^k},\end{split}\]

wobei $\text{Int}(\cdot)$ das Innere einer Menge bezeichnet.

Mit dieser Konstruktion gilt

\[\overline{Q_\varepsilon} \subset Q\subset \bigcup_{k\in\N} Q_k \subset \bigcup_{k\in\N}\text{Int}(Q_k^\varepsilon)\]

daher bilden die Mengen $\text{Int}(Q_k^\varepsilon)$ eine abzählbare offenen Überdeckung der kompakten Menge $\overline{Q_\varepsilon}$. Nach dem Satz von Heine-Borel (Theorem 5.2) existiert somit eine endliche Teilüberdeckung und daher ein $N\in\N$, s.d.,

\[\overline{Q_\varepsilon}\subset \bigcup_{k=1}^N\text{Int}(Q_k^\varepsilon).\]

Für endlich viele Quader können wir nun die Eigenschaften aus Theorem 5.1 benutzen und folgern

\[\begin{split}\lambda^n(Q) -\varepsilon &< \lambda^n(Q_\varepsilon) \leq \lambda^n\left(\bigcup_{k=1}^N\text{Int}(Q_k^\varepsilon\right) \\&\leq \sum_{k=1}^N \lambda^n(Q_k^\varepsilon) < \sum_{k=1}^N \lambda^n(Q_k) + \frac{\varepsilon}{2^k} \\&\leq \sum_{k=1}^\infty \lambda^n(Q_k) + \frac{\varepsilon}{2^k} = \sum_{k=1}^\infty \lambda^n(Q_k) +\varepsilon.\end{split}\]

Da $\varepsilon>0$ beliebig war folgt die Aussage indem wir $\varepsilon$ gegen $0$ schicken.

Sei nun $J\in\mathcal{R}_{\text{Q}}$, wobei $W_1,\ldots,W_N$ paarweise disjunkte halboffene Quader existieren, s.d.,

\[J = \bigcup_{i=1}^N W_i.\]

Dann sehen wir, dass für jedes $i=1,\ldots,N$ die Folge $(Q_k\cap W_i)_{k\in\N}$ erneut eine Folge halboffener Quader mit

\[W_i \subset \bigcup_{k\in\N} Q_k\cap W_i\]

ist und daher können wir den ersten Fall anwenden. Somit folgt

\[\iota(J) = \sum_{i=1}^N \lambda^n(W_i) \leq \sum_{i=1}^N \sum_{k=1}^\infty \lambda^n(W_i\cap Q_k) = \sum_{k=1}^\infty\sum_{i=1}^N \lambda^n(W_i\cap Q_k) = \sum_{k=1}^\infty \lambda^n(Q_k).\]

Analog zum Lebesgue-Inhalt auf $\mathcal{R}_\text{Q}$ in Theorem 5.1 können wir auch für das äußere Lebesgue-Maß ähnliche Eigenschaften zeigen.

Theorem 5.4 (Eigenschaften des äußeren Lebesgue-Maßes)

Das äußere Lebesgue-Maß $\lambda^*$ hat folgende Eigenschaften:

1. $\lambda^*(\emptyset) = 0$

2. Für zwei Mengen $A, B \in \R^n$ mit $A \subset B$ gilt:

\[\lambda^*(A) \leq \lambda^*(B) \qquad (\text{Monotonie}).\]

3. Für eine Folge $(A_k)_{k\in\N}$ von Teilmengen des $\R^n$ gilt:

\[\lambda^*\left( \bigcup_{k=1}^\infty A_k \right) \leq \sum_{k=1}^\infty \lambda^*(A_k) \qquad (\sigma\!-\!\text{Subadditivität}).\]

4. Für $J\in\mathcal{R}_{\text{Q}}$ gilt,

\[\lambda^*(J) = \iota(J).\]

5. Für jede Teilmenge $A \subset \R^n$ und jeden halboffenen Quader $Q$ gilt:

\[\lambda^*(A) = \lambda^*(A \setminus Q) + \lambda^*(A \cap Q).\]

Proof. Ad 1.

Da $\emptyset$ ein halboffener Quader ist gilt

\[0\leq \lambda^\ast(\emptyset) \leq \lambda^n(\emptyset) = 0.\]

Ad 2.

Es bezeichne

\[\mathcal{C}(B) = \{ (Q_i)_{i\in\N}: Q_i \text{ ist halboffener Quader, für }i\in\N, B\subset \bigcup_{i\in\N} Q_i \}\]

die Menge der möglichen Quaderüberdeckungen. Aus $A\subset B$ folgt dann $\mathcal{C}(B) \subset \mathcal{C}(A)$, da jede Überdeckung für $B$ auch eine Überdeckung für $A$ ist und daher

\[\lambda^\ast(A) = \inf_{\sum_{i=1}^\infty:(Q_i)_{i\in\N}\in \mathcal{C}(A)} \leq \inf_{\sum_{i=1}^\infty:(Q_i)_{i\in\N}\in \mathcal{C}(B)} = \lambda^\ast(B).\]

Ad 3.

Sei $\varepsilon>0$ gegeben. Per Definition des Infimums existiert für jede Menge $A_k$ eine Folge von halboffenen Quadern $Q_k^i, i\in\N$, s.d.

\[\begin{split}A_k \subset \bigcup_{i\in\N} Q_i\\ \lambda^\ast(A_k) > \sum_{i=1}^\infty \lambda^n(Q_k^i) - \frac{\varepsilon}{2^k}.\end{split}\]

Dann folgt aber auch, dass

\[\bigcup_{k\in\N} A_k \subset \bigcup_{k\in\N}\bigcup_{i\in\N} Q_k^i\]

und da die rechte Seite erneut eine Quaderüberdeckung ist folgt per Definition

\[\begin{split}\lambda^\ast\left(\bigcup_{k\in\N} A_k\right) &\leq \sum_{k=1}^\infty\sum_{i=1}^\infty \lambda^n(Q_k^i)\\ &< \sum_{k=1}^\infty \lambda^\ast(A_k) - \frac{\varepsilon}{2^k} = \sum_{k=1}^\infty \lambda^\ast(A_k) - \varepsilon.\end{split}\]

Die Aussage folgt indem wir $\varepsilon$ gegen 0 schicken.

Ad 4.

Es sei $J\in\mathcal{R}_{\text{Q}}$, per Definition folgt direkt

\[\lambda^\ast(Q)\leq \iota^\ast(Q).\]

Mit Theorem 5.3 folgt aber auch

\[\iota^\ast(Q)\leq \lambda^\ast(Q).\]

Ad 5.

Es seien zunächst $A$ und $Q$ halboffene Quader, dann ist auch $A\cap Q$ ein halboffener Quader und wir finden paarweise disjunkte halboffene Quader $Q_0,\ldots,Q_N$, s.d.

\[\begin{split}A\cap Q = Q_0\\ A = \bigcup_{i=1}^N Q_i\end{split}\]

und damit

\[\begin{split}\lambda^n(A) &= \lambda^n\left(\bigcup_{i=0}^N Q_i\right)\\ &= \lambda^n(A\cap Q) + \lambda^n\left(\bigcup_{i=1}^N Q_i\right)\\ &\geq \lambda^n(A\cap Q) + \lambda^n(A\setminus Q) \\ &\geq \lambda^n(A).\end{split}\]

Durch die Abschätzung nah oben und nach unten folgt dann

\[\lambda^n(A) = \lambda^n(A\cap Q) + \lambda^n(A\setminus Q).\]

Als nächsten Schritt betrachten wir eine Folge halboffener Quader $(Q_i)_{i\in\N}\mathcal{C}(A)$ und erhalten dann

\[\begin{split}\sum_{i=1}^\infty \lambda^n(Q_i) &= \sum_{i=1}^\infty \lambda^n(Q_i\cap Q) + \lambda^n(Q_i\setminus Q)\\ &\overset{2.}{\geq} \lambda^n(A\cap Q) + \lambda^n(A\setminus Q) &\overset{2.}{\geq} \lambda^n(A).\end{split}\]

Nehmen wir das Infimum über $\mathcal{C}(A)$ folgt

\[\lambda^n(A) \geq \lambda^n(A\cap Q) + \lambda^n(A\setminus Q) \geq \lambda^n(A)\]

und daher die Behauptung.

Als Korollar von Theorem 5.3 und den vorherigen Eigenschaften erhalten wir eine Abschätzung für das äußere Lebesgue-Maß sowohl von oben durch den äußeren Jordan-Inhalt als auch von unten durch den inneren Jordan-Inhalt.

Corollary 5.1

Es sei $A\subset\R^n$, dann gilt

\[\iota_\ast(A) \leq \lambda^\ast(A) \leq \iota^\ast(A).\]

Proof. Für jedes Element $J\in\mathcal{R}_{\text{Q}}$ und beliebige halboffene Quader $Q_i,\i\in\N$, s.d.,

\[J\subset A\subset \bigcup_{i\in\N} Q_i\]

folgt aus Theorem 5.3

\[\lambda^n(J)\leq \sum_{i=1}^\infty Q_i.\]

Dies gilt für jedes $J\in \mathcal{R}_{\text{Q}}$ mit $J\subset A$ und daher insbesondere auch für das Supremum, daher

\[\iota_\ast(A) \leq \sum_{i=1}^\infty Q_i.\]

Diese Aussage gilt wiederum für eine beliebige Folge halboffener Quader welche $A$ überdecken und daher auch für das Infimum, also

\[\iota_\ast(A) \leq \lambda^\ast(A).\]

Die andere Ungleichung folgt per Definition da jede endliche Überdeckung mit halboffenen Quadern (welche im Infimum für $\iota^\ast$ betrachtet werden) auch im Infimum über abzählbare Überdeckungen berücksichtigt wird, daher

\[\lambda^\ast(A)\leq\iota^\ast(A).\]

Die obige Eigenschaft liefert zusätzlich die Aussage, dass für Jordan-messbare Mengen $A$ gilt

\[\iota(A)\leq\lambda^\ast(A)\leq\iota(A)\Rightarrow \lambda^\ast(A) = \iota(A).\]

Remark 5.6 (Wirkung von Transformationen auf das äußere Lebesgue Maß)

Eine besondere Eigenschaft des äußeren Lebesgue Maßes ist es, dass es bewegungsinvariant ist, d.h., dass es unter Translationen und Rotationen den gleichen Wert behält. Dies ist für viele Anwendungen eine fundamentale Eigenschaft. Die folgende Bemerkung hält die Wirkung von geometrischen Transformationen auf das äußere Lebesgue Maß fest.

1. Sei $A \subset \R^n$ eine beliebige Teilmenge und $a \in \R^n$ ein beliebiger Vektor. Dann ist das äußere Lebesgue Maß translationsinvariant unter der Wirkung von $a$, d.h., es gilt

\[\lambda^*(A + a) = \lambda^*(A).\]

Außerdem gilt, dass die Teilmenge $A$ genau dann Lebesgue-messbar ist, wenn die verschobene Teilmenge $A + a$ Lebesgue-messbar ist.

2. Sei $A \subset \R^n$ eine beliebige Teilmenge und $M \in \R^{n\times n}$ eine beliebige Matrix. Dann gilt für das äußere Lebesgue Maß der folgende Zusammenhang unter der Wirkung der linearen Transformation $M$

\[\lambda^*(MA) = |\!\operatorname{det}(M)| \, \lambda^*(A).\]

Das heißt insbesondere, dass das äußere Lebesgue Maß invariant unter Transformationen der orthogonalen Gruppe (z.B. Rotationen und Spiegelungen) ist, da für diese Transformationen $|\!\operatorname{det}(M)| = 1$ gilt (siehe Kapitel 3.6 in [Ten21]).

Außerdem gilt, dass die Teilmenge $A$ genau dann Lebesgue-messbar ist, wenn die linear transformierte Teilmenge $MA$ Lebesgue-messbar ist.

5.1.4.3. Nullmengen¶

Eine relevante Klasse von Teilmengen des $\R^n$ bilden sogenannten Lebesgue-Nullmengen.

Definition 5.16 (Lebesgue-Nullmengen)

Eine Teilmenge $N \subset \R^n$ eine (Lebesgue-)Nullmenge, falls ihr äußeres Lebesgue-Maß Null ist, d.h., es gilt

\[\lambda^*(N) = 0.\]

Für die Klasse der Nullmengen können wir folgende Eigenschaften zeigen.

Lemma 5.8 (Eigenschaften von Lebesgue-Nullmengen)

Für Lebesgue-Nullmengen gelten die folgenden Eigenschaften:

Sei $(N_n)_{n\in\N}$ eine Familie von Nullmengen. Dann ist auch $\bigcup_{n\in\N} N_n$ eine Nullmenge.
Alle abzählbaren Mengen sind Nullmengen.
Alle Teilmengen von Nullmengen sind Nullmengen.

Proof.

Ad 1.

Auf Grund der $\sigma$-Subadditivität des äußeren Lebesgue-Maßes folgt direkt

\[0 \leq \mu^* \left( \bigcup_{n\in\N} N_n \right) \leq \sum_{n\in\N} \mu^*(N_n) = 0.\]

Da $\mu^* \left( \bigcup_{n\in\N} N_n \right)$ gilt ist also $\bigcup_{n\in\N} N_n$ auch eine Nullmenge.

Ad 2.

Es sei $A\subset\R^d$ eine abzählbare Menge, d.h., es existiert eine Folge $(a_k)_{k\in\N}\subset\R^d$, s.d.,

\[A = \bigcup_{k\in\N} a_k.\]

Es sei nun $\varepsilon>0$ gegeben, dann wählen wir die Folge halboffener Quader

\[Q_k := (a_k - \frac{\varepsilon}{2^k},a_k]\]

s.d.,

\[A\subset \bigcup_{k\in\N} Q_k.\]

Dann folgt aber,

\[\lambda^\ast(A) \leq \sum_{k\in\N} \lambda^n(Q_k) = \sum_{k\in\N} \frac{\varepsilon}{2^k} = \varepsilon.\]

Wir können nun $\varepsilon$ gegen 0 schicken und erhalte die Aussage.

Ad 3.

Es sei $N$ eine Nullmenge und $A\subset N$, dann folgt aus der Monotonie

\[0\leq \lambda^\ast(A)\leq \lambda^\ast(N) = 0.\]

Intuitiv könnten man meinen, dass lediglich abzählbare MEngen Lebesgue Nullmengen sind, dies ist jedoch nicht der Fall. Ein Beispiel ist die canto-Menge welche überabzählbar ist, aber Lebesgue-Maß null hat.

5.1.4.4. Das äußere Maß ist kein Maß¶

Für das äußere Lebesgue Maß kann man einige Eigenchaften zeigen (siehe Theorem 5.4) welche zwar eine Maß erinnern. Der größte Unterschied bisher ist, dass wir nur $\sigma$-Subadditivität und nicht $\sigma$-Additivität zeigen konnten. Insbesondere arbeitet das äußere Maß auf der gesamten Potenzmenge $2^{\R^d}$ und nicht auf einer kleineren $\sigma$-Algebra, man könnte also vermuten, dass diese Menge zu groß ist um $\sigma$-Additivität zeigen zu können, was tatsächlich der Fall ist.

Um das zu sehen betrachten wir die sogenannte Vitali Menge auf $\R$.

Für zwei Punkte $x,y\in\R$ definiert man die Äquivalenzrelation

\[x \sim y \quad \Leftrightarrow \quad x-y \in \Q.\]

d.h. zwei Punkte gehören der selben Äquivalenzklasse an sofern ihre Differenz rational ist. Es gilt also

\[[x] = \{y: y-x\in\Q\}\]

jede Klasse $[x]$ ist abzählbar und $[0] = \Q$. Falls $[x]\cap [y]\neq \emptyset$, so folgt, dass ein $z\in[x]\cap [y]$ existiert und damit

\[\begin{split}\left. \begin{matrix} z-x\in\Q\\ z-y\in\Q\\ \end{matrix} \right\} \Rightarrow x-y\in\Q\Rightarrow [x]=[y],\end{split}\]

daher sind zwei Äquivalenzklassen entweder gleich oder disjunkt. Da aber

\[\R = \bigcup_{x\in\R} [x]\]

gilt, muss es überabzählbar viele disjunkte Äquivalenzklassen geben, ansonsten wäre $\R$ selbst abzählbar. Mithilfe des Auswahl-Axioms können wir nun für jede einzelne Äquivalenzklasse einen Repräsentanten wählen, wobei wir die Menge der Repräsentanten $V$ als Vitali-Menge bezeichnen. Zwei Elemente $x,y\in V, x\neq y$ unterscheiden sich stets um eine irrationale Zahl, denn

\[x-y\in\Q \Rightarrow [x] = [y]\]

ist ein Widerspruch zur Konstruktion.

Es sei nun $(q_k)_{k\in\N}$ eine Abzählung der rationalen Zahlen und definiere die verschobenen Vitali Mengen

\[V_k :=\{x+q_k: x\in V\}.\]

Lemma 5.9

Mit den obigen Definitionen gilt

$\lambda^\ast(V) = \lambda^\ast(V_k)$ für alle $k\in\N$,
$V_k\cap V_l=\emptyset$ für $k\neq l$,
$\bigcup_{k\in\N} V_k = \R$.

Proof.

Ad 1.

Diese Tatsache folgt, da das äußere Lebesgue-Maß Translationsinvariant ist, siehe Remark 5.6.

Ad 2.

Für $x,y\in V$ gilt

\[\begin{split}x + q_k = y + q_l&\Rightarrow x-y\in\Q\\ \Rightarrow [x]=[y]&\Rightarrow x=y\\ \Rightarrow q_k=q_l&\Rightarrow k=l\end{split}\]

wobei wir in der zweiten Zeile erneut ausnutzen, dass die Elemente aus $V$ jeweils disjunkte Äquivalenzklassen erzeugen.

Ad 3.

Trivialerweise gilt

\[\bigcup_{k\in\N} V_k \subset \R.\]

Andererseits sei $x\in\R$ dann existiert $v\in V$ s.d. $[v] = [x]$. Somit gilt $x-v\in\Q$ und es existiert $k\in\N$, s.d.

\[q_k = x-v.\]

Somit folgt $x=v+q_k\in V_k$ und daher $x\in\bigcup_{k\in\N} V_k$.

Mithilfe einer Vitali-Menge können wir nun die $\sigma$-Additivität des äußeren Lebesgue-Maßes zum Widerspruch führen.

Lemma 5.10

Das äußere Lebesgue-Maß $\lambda^\ast$ ist nicht $\sigma$-Additiv auf $2^{\R}$.

Proof. Annahme: Das äußere Lebesgue-Maß sei $\sigma$-Additiv auf $2^{\R}$.

Die Mengen $V_k$ sind paarweise disjunkt und überdecken $\R$, daher folgt

\[0<\lambda^\ast(\R) = \lambda^\ast(\bigcup_{k\in\N} V_k) = \sum_{k\in\N} \lambda^\ast(V_k) = \sum_{k\in\N} \lambda^\ast(V)\]

und daher $\lambda^\ast(V)>0$. Diese Folgerung wollen wir nun zum Widerspruch führen. Dazu betrachten wir die folge halboffener Quader $Q_k:=(k,k]$ und erkennen unter Ausnutzung endlicher Additivität, dass

\[\lambda^\ast(V) \geq \lambda^\ast\left(V \cap \bigcup_{k=1}^N Q_k\right) = \sum_{k=1}^N \lambda^\ast(V\cap Q_k).\]

Somit folgt mithilfe der $\sigma$-Subadditivität

\[\lambda^\ast(V) \geq \sum_{k=1}^\infty \lambda^\ast(V\cap Q_k) \geq \lambda^\ast\left(\bigcup_{k\in\N} V\cap Q_k\right) = \lambda^\ast(V).\]

Da wir $\lambda^\ast(V)>0$ folgern konnten, muss daher ein $N\in\N$ existieren, s.d.,

\[\lambda^\ast(V\cap Q_N) >0.\]

Analog zum Beweis, dass die $V_k$ paarweise disjunkt sind, folgert man auch, dass die Mengen $\frac{1}{m}+(V\cap Q_N)$ für verschieden $m\in\N$ paarweise disjunkt sind und wegen der Translationsinvarianz folgt

\[\lambda^\ast(\frac{1}{m}+(V\cap Q_N)) = \lambda^\ast((V\cap Q_N)) >0.\]

Wir erkennen allerdings, dass

\[\bigcup_{m\in\N} \frac{1}{m}+(V\cap Q_N) \subset (-N,N+1]\]

und nutzen wir nun erneut die angenommene $\sigma$-Additivität so erhalten wir

\[\infty = \sum_{m=1}^\infty \lambda^\ast(\frac{1}{m}+(V\cap Q_N)) = \lambda^\ast\left(\bigcup_{m\in\N} \frac{1}{m}+(V\cap Q_N) \right)\leq \lambda^\ast((-N,N+1]) = 2N + 1\]

und somit

\[\infty \leq 2N + 1\]

was ein Widerspruch ist. Daher ist die Annahme der $\sigma$-Additivität falsch.

Ähnliche Konstruktionen können auch allgemein für $\R^n$ durchgeführt werden. Man hat allgemein die Aussage, dass $\lambda^\ast$ auf $\R^n$ kein Maß ist.

5.1.4.5. Das Lebesgue-Maße¶

Der vorherige Abschnitt zeigt, dass die Potenzmenge $2^{\R^n}$ zu groß ist, d.h. auf dieser $\sigma$-Algebra ist $\lambda^\ast$ kein Maß. Deshalb wollen wir nun eine Klasse messbarer Mengen definieren, welche dann eine kleinere $\sigma$-Algebra liefert.

Remark 5.7 (Das Jordan-Konzept)

Eine mögliche Idee um messbare Mengen zu definieren haben wir bereits beim Jordan-Inhalt kennengelernt. Hierbei wird zusätzlich zum äußeren Maß ein inneres Maß definiert. Beim Übergang vom äußeren Jordan-Inhalt zum äußeren Lebesgue-Maß werden endliche Vereinigungen durch unendliche ersetzt, weshalb man versuchen könnte, das nun auch hier zu tun, indem man das innere Lebesgue-Maß auch über unendliche Vereinigungen definiert

\[\lambda_\ast(A) := \sup\left\{\sum_{i=1}^\infty Q_i: \bigcup_{i\in\N} Q_i \subset A, Q_i\text{ disjunkte halboffener Quader}\right\}.\]

Offensichtlich folgt mit dieser Definition

\[\iota_\ast(A)\leq \lambda_\ast(A)\]

da das Supremum über mehr Ausschöpfungen gebildet wird. Nun sei aber $Q_i$ eine beliebiger Folge halboffener Quader, welche $A$ von innen ausschöpfen, dann gilt für jedes $N\in\N$

\[\iota_\ast(A) \geq \sum_{i=1}^N \lambda^n(Q_i)\]

und daher

\[\iota_\ast(A)\geq \sum_{i=1}^\infty \lambda^n(Q_i).\]

Diese Ungleichung erhalten wir deshalb so einfach, da für jedes $N\in\N$ auch $\bigcup_{i=1}^N Q_i\subset A$ gilt. Beim äußern Maßen konnten wir aber andersherum nicht einfach aus $A\subset \bigcup_{i=1}^\infty W_i$ auch $A\subset \bigcup_{i=1}^N W_i$ folgern.

Da die obige Ungleichung für beliebig Folgen halboffener Quader gilt, folgt

\[\iota_\ast(A) \geq \lambda_\ast(A).\]

Wir erkennen also, dass für das innere Maß keinen Unterschied macht ob wir endliche oder unendliche Vereinigungen betrachten.

Würden wir Messbarkeit über die Bedingung

\[\lambda_\ast(A)=\lambda^\ast(A)\]

definieren erhielten wir erneut keine $\sigma$-Algebra. Denn für die Menge $A=[0,1]\setminus\Q$ gilt

\[J\in\mathcal{R}_{\text{Q}}, J\subset A\Rightarrow J=\emptyset\]

und daher $\lambda_\ast(J) = 0$. Der Trick die Menge mit kleinen Quadern zu approximieren wie beim äußeren Maß funktioniert auch nicht, da wir in diesem Fall jeweils die Teilmengen Bedingung verletzt wäre.

Es gilt aber

\[\lambda^\ast(A) = \lambda^\ast([0,1]) - \underbrace{\lambda^\ast(\Q)}_{=0} = 1\]

und daher wäre $A$ nicht messbar, obwohl sowohl $\Q$, als auch $[0,1]$ messbar wären. Damit hätten wir erneut keine $\sigma$-Algebra konstruiert.

Es gibt verschiedene Ansätze Lebesgue-Messbarkeit zu definieren (welche alle äquivalent sind), wir wählen im Folgenden das Konzept von Carathéodory.

Definition 5.17 (Lebesgue-Maß)

Wir nennen eine Teilmenge $A \subset \R^n$ Lebesgue-messbar, genau dann wenn für alle Teilmengen $E \subset \R^n$ gilt:

\[\lambda^*(E) = \lambda^*(E \cap A) + \lambda^*(E \setminus A).\]

Wir notieren die Menge der Lebesgue-messbaren Mengen als

\[\mathcal{A}(\R^n) = \lbrace A \subset \R^n : A \text{ ist Lebesgue-messbar } \rbrace\]

Wir definieren das Lebesgue-Maß $\lambda \colon \mathcal{A} \rightarrow [0,\infty]$ messbarer Mengen durch

\[\lambda(A) = \lambda^*(A).\]

Remark 5.8

Es ist wichtig zu bemerken, dass diese Bedingung eine Einschränkung ist, da das äußere Lebesgue-Maß nicht additiv ist auf $2^{\R^n}$, es gilt lediglich

\[\lambda^*(E) \leq \lambda^*(E \cap A) + \lambda^*(E \setminus A).\]

für alle $A,E\subset\R^d$. Aus diesem Grund scheint die Einschränkung sinnvoll zu sein um Additivität zu erhalten.

Wir betrachten im Folgenden verschiedene Beispiele messbarer Mengen, was zeigt, dass $\mathcal{A}\neq \emptyset$.

Lemma 5.11 (Lebesgue-messbare Mengen)

Jede Lebesgue-Nullmenge ist Lebesgue-messbar, insbesondere ist $\emptyset$ Lebesgue-messbar.
Jeder halboffene Quader ist messbar.

Proof. ** Ad 1.**

Es sei $N$ eine Lebesgue-Nullmenge und $E\subset\R^d$, dann gilt

\[\lambda^\ast(E) \leq \underbrace{\lambda^\ast(E\cap\N)}_{=0} + \lambda^\ast(E\setminus N)\leq \lambda^\ast(E)\]

und daher $\lambda^\ast(E) = \lambda^\ast(E\cap\N) + \lambda^\ast(E\setminus N)$.

Ad 2.

Folgt aus Theorem 5.4 Eigenschaft 4.

Weiterhin erhält man über den Begriff der Lebesgue-messbarkeit endlich die erhoffte $\sigma$-Algebra Struktur.

Lemma 5.12

Die Klasse der Lebesgue-messbaren Mengen $\mathcal{A}$ bildet eine $\sigma$-Algebra.

Proof. 1. Von Lemma 5.11 erhalten wir zunächst, dass $\emptyset\in\mathcal{A}$.

2. Weiterhin sei $A\in\mathcal{A}$ messbar und $E\subset\R^d$ beliebig, dann gilt

\[\lambda^\ast(E) = \lambda^\ast(\underbrace{A\cap E}_{=E\setminus A^C}) + \lambda^\ast(\underbrace{E\setminus A}_{=E\cap A^C}) = \lambda^\ast(E\setminus A^C) + \lambda^\ast(E\cap A^c) \]

und daher ist auch $A^C\in\mathcal{A}$.

3. Wir zeigen zunächst, dass $\mathcal{A}$ unter endlichen Vereinigungen, Schnitten und Differenzen abgeschlossen ist.

Es seien $A,B\in\mathcal{A}$ und $E\subset\R^d$ dann gilt

\[\begin{split}\lambda^\ast(E) &= \lambda^\ast(E\cap A) + \underbrace{\lambda^\ast(E\setminus A)}_{\text{wende Messbarkeit von} B\text{ an}}\\ &=\lambda^\ast(E\cap A) + \lambda^\ast((E\setminus A)\cap B) + \lambda^\ast((E\setminus A)\setminus B)\\ &= \underbrace{\lambda^\ast(E\cap (A\cup B)\cap A) + \lambda^\ast((E\cap A\cup B)\setminus A)}_{\text{wende Messbarket von } A \text{ an}} + \lambda^\ast(E\setminus(A\cup B))\\ &= \lambda^\ast(E\cap (A\cup B)) + \lambda^\ast(E\setminus(A\cup B))\end{split}\]

und daher ist $A\cup B$ messbar. Weiterhin folgt $A\cap B = (A^C\cup B^C)^C\in\mathcal{A}$ und daher auch $A\cap B\in\mathcal{A}$. Außerdem gilt $A\setminus B = A\cap B^C$ und somit auch $A\setminus B\in\mathcal{A}$.

4. Sei nun $A_i\in\mathcal{A}$ für $i\in\N$ eine disjunkte Folge von Mengen und setze $A=\bigcup_{i\in\N} A_i$. Unter Ausnutzung von $A_1\in\mathcal{A}$ haben wir für $E\subset\R^d$

\[\begin{split}\lambda^\ast(E\cap (A_1\cup A_2)) &= \lambda^\ast(E\cap(A_1\cup A_2)\cap A_1) + \lambda^\ast(E\cap(A_1\cup A_2)\setminus A_1)\\ &= \lambda^\ast(E\cap A_1) + \lambda^\ast(E\cap A_2)\end{split}\]

und somit gilt für endliche Vereinigungen

\[\lambda^\ast(E\cap \bigcup_{i=1}^N A_i) = \sum_{i=1}^N \lambda^\ast(E\cap A_i).\]

Mit Monotonie folgt dann für jedes $N\in\N$

\[\lambda^\ast(E\cap A)\geq \lambda^\ast(E\cap \bigcup_{i=1}^N A_i) = \sum_{i=1}^N \lambda^\ast(E\cap A_i)\]

und daher mit der $\sigma$-Subadditivität

(5.1)¶\[\lambda^\ast(E\cap A) \geq \sum_{i=1}^\infty \lambda^\ast(E\cap A_i)\geq \lambda^\ast\left(\bigcup_{i\in\N} E\cap A_i\right) = \lambda^\ast(E\cap A).\]

Weiterhin wissen wir nach 3., dass endliche Vereinigungen messbarer Mengen messbar sind, daher

\[\begin{split}\lambda^\ast(E) &= \lambda^\ast\left(E\cap \bigcup_{i=1}^N A_i\right) + \lambda^\ast\left(E\setminus \bigcup_{i=1}^N A_i\right)\\ &\geq \sum_{i=1}^N \lambda^\ast(E\cap A_i) + \lambda^\ast(E\setminus A)\end{split}\]

für alle $N\in\N$ und somit

\[\lambda^\ast(E)\geq \sum_{i=1}^\infty \lambda^\ast(E\cap A_i) + \lambda^\ast(E\setminus A)\geq \lambda^\ast(E\cap A) + \lambda^\ast(E\setminus A) \geq \lambda^\ast(E).\]

Daraus schließen wir mit , dass :eqref:`eq:LebesgueAlgebra`

\[\lambda^\ast(E) = \sum_{i=1}^\infty \lambda^\ast(E\cap A_i) + \lambda^\ast(E\setminus A) = \lambda^\ast(E\cap A) + \lambda^\ast(E\setminus A).\]

5.\ Es bleibt die Aussage für eine belibige nicht notwendigerweise disjunkte Folge $A_i\in\mathcal{A}, i\in\N$ zu zeigen. Dazu definieren wir die Mengen $B_1:=A_1$,

\[B_k := A_i\setminus \left(\bigcup_{i=1}^k B_i \right)\]

wobei wir erkennen, dass die $B_i$ paarweise disjunkt sind und insbesondere gilt

\[\bigcup_{k\in\N} B_k = \bigcup_{i\in\N} A_i.\]

Nach 4. ist damit auch diese Vereinigung messbar.

Mit dieser Aussage können wir weitere messbare Mengen identifizieren.

Lemma 5.13

Offene und abgeschlossene Teilmengen des $\R^n$ sind Lebesgue-messbar.

Proof. Es sei $U\subset\R^d$ offen, wir betrachten die Menge

\[\bigcup_{a,b\in \Q^d, (a,b]\subset U} (a,b]\subset U\]

Sei nun $x\in U$, dann existiert auch $a,b\in\Q^d$, s.d. $x\in(a,b]\subset U$ und somit $x\in\bigcup_{a,b\in \Q^d, (a,b]\subset U}$, woraus wir schließen

\[\bigcup_{a,b\in \Q^d, (a,b]\subset U} (a,b] = U.\]

Somit ist $U$ abzählbare Vereinigung messbarer Mengen und daher selbst messbar.

Abgeschlossene Mengen sind als Komplemente offener und daher messbarer Mengen, selbst messbar.

Da wir nun eine $\sigma$-Algebra zu Verfügung haben können wir ein Maß definieren.

Definition 5.18 (Lebesgue-Maß)

Wir definieren das Lebesgue-Maß $\lambda^n:\mathcal{A}\to[0,\infty]$ über die Einschränkung des äußeren Maßes, d.h.,

\[\lambda^n(A):= \lambda^\ast(A)\text{ für } A\in\mathcal{A}.\]

Gefahr

ToDo

Theorem 5.5 (Regularität des Lebesgue Maßes)

Das Lebesgue Maß ist von außen und innen regulär im Sinne von Definition 5.6, d.h., für jede Lebesgue-messbare Teilmenge $A \subset \R^n$ gilt

1. für jedes $\epsilon > 0$ existiert eine offene Menge $U$ mit $A \subset U$ für die gilt $\mu(U \setminus A) < \epsilon$,

2. für jedes $\epsilon > 0$ existiert eine abgeschlossene Menge $F$ mit $F \subset A$ für die gilt $\mu(A \setminus F) < \epsilon$.

Proof. ToDo.

Theorem 5.6 (Charakterisierung Lebesgue-messbarer Mengen)

Die folgenden drei Aussagen sind äquivalent, so dass sie eine Charakterisierung der Lebesgue-messbaren Mengen darstellen.

1. Eine Teilmenge $A \subset \R^n$ ist Lebesgue messbar.

2. Für jedes $\epsilon > 0$ existiert eine offene Menge $U$ und eine abgeschlossene Menge $F$, so dass $F \subset A \subset U$ und es gilt $\mu(U \setminus F) < \epsilon$.

3. Für jedes $\epsilon > 0$ existiert eine offene Menge $U$ mit $A \subset U$ für die gilt $\mu(U \setminus A) < \epsilon$.

Proof. ToDo

Man kann für die Borel-$\sigma$-Algebra von $\R^n$ zeigen, dass gilt

\[\B(\R^n) = \sigma(\lbrace A \subset \R^n \text{ offen }\rbrace) ) = \sigma(\lbrace A \subset \R^n \text{ abgeschlossen }\rbrace)\]

Die letzte Gleichung gilt, da $\sigma$-Algebren abgeschlossen unter Komplementbildung sind. Zusammen mit Lemma 5.13 folgt dann schon, dass die Borel-$\sigma$-Algebra $\B(\R^n)$ eine Teilmenge der Lebesgue messbaren Mengen ist. Der folgende Satz zeigt, dass es eine echte Teilmenge ist indem er den Unterschied der Mengen als Lebesgue Nullmengen charaterisiert.

Theorem 5.7

Eine Teilmenge $A \subset \R^n$ ist genau dann Lebesgue-messbar, wenn eine Teilmenge $B \in \B(\R^n)$ und eine Nullmenge $N \subset \R^n$ existiert, so dass $A = B \cup N$ ist, wobei $B\cap N=\emptyset$.

Proof. ToDo

Mathematik für Physikstudierende C

Maßtheorie

Inhalt

5.1. Maßtheorie¶

5.1.1. Mengensysteme¶

5.1.2. Maße¶

5.1.3. Borel-Maße¶

5.1.3.1. Erzeugte Topologien¶

5.1.3.2. Eigenschaften von Borel-Maßen¶

5.1.4. Das Lebesgue Maß¶

5.1.4.1. Der Jordan-Inhalt und Jordan-messbare Mengen¶

5.1.4.2. Das äußere Lebesgue-Maß¶

5.1.4.3. Nullmengen¶

5.1.4.4. Das äußere Maß ist kein Maß¶

5.1.4.5. Das Lebesgue-Maße¶