5.3. Integrationstechniken¶

In diesem Abschnitt beschäftigen wir uns mit Rechenmethoden und Rechenregeln, die es uns erlauben Funktionen mehrerer Variablen bezüglich des Lebesgue-Maßes zu integrieren. Insbesondere lernen wir dadurch Verfahren kennen um Volumina und Flächen zu berechnen. Um diese Regeln formal zu zeigen benötigen wir zunächst etwas Theorie.

5.3.1. Produktalgebren¶

Für zwei Messräume \((\Omega_1,\Sigma_1), (\Omega_2,\Sigma_2)\) wollen wir nun einen Produktraum erhalten. Hierbei werden wir auf Konzepte des Tensorproduktes zurückgreifen und benutzen deshalb die gleiche Notation. Wir definieren dann die Produkt-\(\sigma\)-Algebra,

\[\Sigma_1\otimes\Sigma_2 := \sigma\left(\Sigma_1\times\Sigma_2\right),\]

wobei

\[\Sigma_1\times\Sigma_2 = \left\{A_1\times A_2: A_1\in\Sigma_1, A_2\in\Sigma_2\right\}.\]

Wir arbeiten nicht auf Vektorräumen darum konstruieren wir kein Tensorprodukt im Sinnen von Abschnitt 3.2, aber die grundlegenden Konzepte sind ähnlich, weshalb es üblich ist, hier diese Notation zu verwenden. Weiterhin erkennen wir, dass mit dieser Konstruktion \(\Sigma_1\otimes\Sigma_2 \) eine \(\sigma\)-Algebra auf \(\Omega_1\times\Omega_2\) ist.

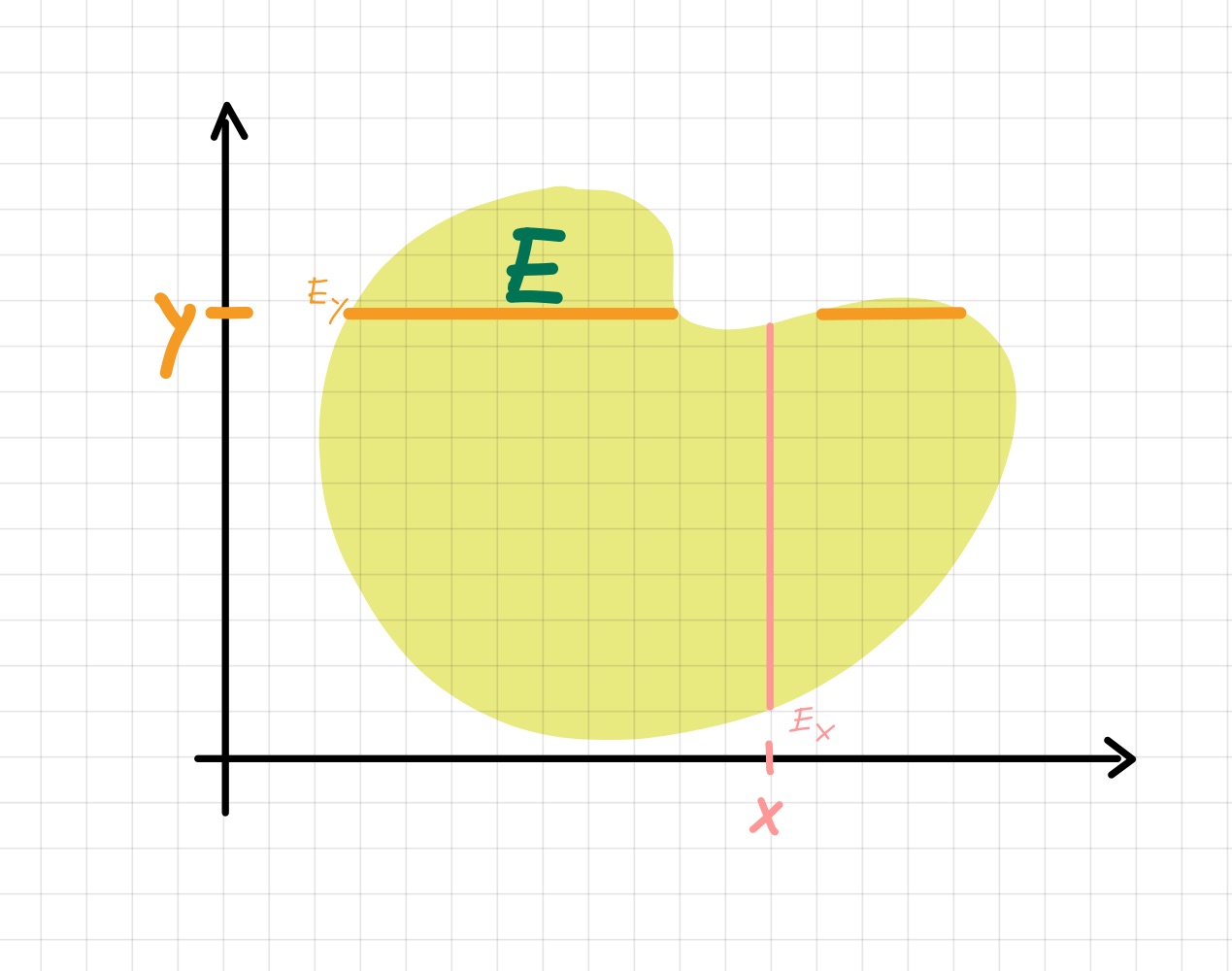
Abb. 5.5 Visualisierung von Mengenschnitten.¶

Für eine Menge \(E\subset\Omega_1\times\Omega_2\) betrachtet man in diesem Kontext oft sogenannte Schnitte

\[\begin{split}E_x := \{y\in \Omega_2: (x,y)\in E\}\subset\Omega_2\\ E^y := \{x\in \Omega_1: (x,y)\in E\}\subset\Omega_1\end{split}\]

wofür man folgende Aussage hat.

Lemma 5.24

Es seien \((\Omega_1,\Sigma_1), (\Omega_2,\Sigma_2)\) Messräume, dann gilt für eine Menge \(E\in \Sigma_1\otimes\Sigma_2\), dass \(E_x\in \Sigma_2, E_y\in\Sigma_1\) für alle \(x\in\Omega_1,y\in\Omega_2\).

Proof. Wir betrachten das Teilmengensystem

\[\M = \{E\subset\Omega_1\times\Omega_2: E_x\in\Sigma_2, E^y\in\Sigma_1,\quad\forall x\in\Omega_1, y\in\Omega_2\}\]

d.h. alle Mengen, welche die gewünschte Bedingung erfüllen. Wir sehen, dass für \(A\in\Sigma_1,B\in\Sigma_2\) gilt

\[\begin{split}(A\times B)_x = \begin{cases} B &\text{ falls }x\in A\\ \emptyset &\text{ sonst} \end{cases}\end{split}\]

und daher \((A\times B)_x\in\Sigma_2\) für alle \(x\in\Omega_1\). Analog zeigt man \((A\times B)^y\in\Sigma_1\) für alle \(y\in\Omega_2\) und daher gilt

\[\Sigma_1\times\Sigma_2\subset \M.\]

Weiterhin ist \(\M\) eine \(\sigma\)-Algebra, denn es gilt \(\emptyset\in\M\), weiterhin \((E^C)_x = (E_x)^C\)und analog \((E^C)^y= (E^y)^C\) und daher gilt

\[E\in\M\Rightarrow E^C\in\M.\]

Weiterhin gilt für eine Folge von Mengen \(E_i\in\M,i\in\N\)

\[\left(\bigcup_{i\in\N} E_i\right)_x = \bigcup_{i\in\N} (E_i)_x\]

analog für den anderen Schnitt und daher

\[\bigcup_{i\in\N} E_i\in\M.\]

Somit folgt

\[\Sigma_1\otimes\Sigma_2=\sigma(\Sigma_1\times\Sigma_2)\subset \sigma(\M) = \M.\]

Speziell für \(\Omega_1=\R^n, \Omega_2=\R^m\) könnte man sich nun fragen wie sich die Produkt-Algebra für die bekannten Borel und Lebesgue Algebren verhält. Zumindest für die Borel \(\sigma\)-Algebra haben wir folgende Aussage.

Lemma 5.25

Für \(n,m\in\N\) gilt

\[\B(\R^n)\otimes \B(\R^m) = \B(\R^{n+m}).\]

Proof. Offensichtlich gilt für den Mengen-Ring

\[\mathcal{R}(\R^{n+m})=\left\{\bigcup_{i=1}^N Q_i: Q_i\subset\R^{n+m}\text{ ist halboffener Quader} \right\},\]

dass

\[\mathcal{R}(\R^{n+m})\subset \B(\R^n)\otimes \B(\R^m).\]

Weiterhin wissen wir aber auch nach Erzeugte Topologien, dass \(\sigma(\mathcal{R}(\R^{n+m})) = \B(\R^{n+m})\) und somit

\[\B(\R^{n+m})\subset \B(\R^n)\otimes \B(\R^m).\]

Für die andere Richtung sei \(A_1\in\B(\R^n) A_2\in\B(\R^m)\), dann gilt

\[A_1\times A_2 = \left(A_1\times\R^m\right) \cap (\R^n\times A_2) =\pi_1^{-1}(A_1) \cap \pi_2^{-1}(A_2)\]

wobei \(\pi_1:\R^{n+m}\to\R^n,\pi_2:\R^{n+m}\to\R^m\) die Projektionen

\[\begin{split}\pi_1(z_1,\ldots,z_{n+m})&= (z_1,\ldots, z_n)\\ \pi_2(z_1,\ldots,z_{n+m})&= (z_{n+1},\ldots, z_{n+m})\end{split}\]

sind. Da Projektionen stetig sind, sind sie Borel-messbar nach ?? und daher gilt

\[\begin{split}\pi_1^{-1}(A_1)\in B(\R^{n+m})\\ \pi_2^{-1}(A_2)\in B(\R^{n+m}).\end{split}\]

Daraus folgern wir, dass

\[A_1\times A_2 \in \B(\R^{n+m})\]

und somit

\[\B(\R^n)\otimes \B(\R^m)\subset\B(\R^{n+m}).\]

Für die Lebesgue \(\sigma\)-Algebren gilt diese Identität nicht, allgemein kann man zeigen, dass

\[\mathcal{A}(\R^n)\otimes\mathcal{A}(\R^m)\subset \mathcal{A}(\R^{n+m})\]

allerdings ist die Menge auf der rechten Seite echt größer wie das folgende Beispiel zeigt.

Example 5.5

Wir betrachten die zwei Lebesgue-Algebren für \(n=m=1\), dh. \(\mathcal{A}(\R)\). Nach Abschnitt 5.1.4.4 gibt es Mengen \(V\subset\R\) sogenannte Vitali-Mengen s.d. \(V\not\in\mathcal{A}(\R)\). Weiterhin erkennen wir, dass für das Lebesgue-Maß auf \(\R^2\) folgt, dass

\[\lambda^{2}(V\times\{0\}) = 0\]

dies folgt mit der Argumentation aus Aufgabe??. Daher ist \(V\times\{0\}\in \mathcal{A}(\R^2)\) da es eine Nullmenge ist.

Wir erkennen aber, dass sich \(V\) als Schnitt dieser Produkt-Menge darstellen lässt, nämlich

\[V = (V\times\{0\})^0\]

wäre nun \(V\times\{0\}\in \mathcal{A}(\R)\otimes\mathcal{A}(\R)\) so würde mit Lemma 5.24 folgen, dass auch der Schnitt \(V\in\mathcal{A}(\R)\) gilt, was ein Widerspruch ist, daher

\[V\times\{0\} \not\in \mathcal{A}(\R)\otimes\mathcal{A}(\R).\]

Das abstrakte Konzept, welches sich hinter diesem Beispiel verbirgt wir mit dem Begriff Vollständigkeit eines Maßes bezeichnet.

Definition 5.25

Ein Maßraum \((\Omega,\Sigma,\mu)\) heißt vollständig, falls für jede \(\mu\)-Nullmenge \(N\in\Sigma, \mu(N)=0\) gilt

\[A\subset N \Rightarrow A\in \Sigma.\]

Remark 5.11

Wir wissen, dass jede Menge die bezüglich des äußeren Maßes \(\lambda^\ast\) eine Nullmenge ist auch Lebesgue-messbar ist. Daher ist das Lebesgue-Maß ein vollständiges Maß.

Weiterhin lässt sich ein beliebiges Maß vervollständigen, indem wir die \(\sigma\)-Algebra

\[\overline{\Sigma}:=\{A\cup N: A\in\Sigma, N\subset B\in\Sigma\text{ mit }\mu(B)=0\}\]

betrachten zusammen mit dem Maß

\[\overline{\mu}(B)= \overline{\mu}(A\cup N):= \mu(A).\]

Hier lässt sich nun folgendes zeigen.

Lemma 5.26

Für \(n,m\in\N\) gilt

\[\overline{\mathcal{A}(\R^n)\otimes\mathcal{A}(\R^m)}= \mathcal{A}(\R^{n+m}).\]

Proof. Siehe z.B. [Bog07] Theorem 1.5.6.

5.3.2. Produktmaße¶

Wir wollen nun Maße auf der Produktalgebra betrachten.

Definition 5.26 (Produktmaß)

Es seien \((\Omega_1,\Sigma_1,\mu_1), (\Omega_2,\Sigma_2,\mu_2)\) zwei Maßräume, dann heißt ein Maß \(\mu\) auf dem Messraum \((\Sigma_1\otimes\Sigma_2, \Omega_1\times\Omega_2)\) Produktmaß, falls

\[\mu(A_1\times A_2) = \mu_1(A_1)\cdot\mu_2(A_2)\quad\forall A_1\in\Sigma_1, A_2\in\Sigma_2.\]

Remark 5.12

In Grassmann-Algebra haben wir das Tensorprodukt zweier lineare Abbildungen \(T_1,T_2\) definiert über

\[(T_1\otimes T_2)(v_1,v_2) := T_1(v_1)\cdot T_2(v_2).\]

Es sei hier erwähnt, dass das Maß keine lineare Abbildung ist, insbesondere haben wir keinen Vektorraum gegeben. Die Produktstruktur ist trotzdem ähnlich, weshalb eine gewisse Analogie zwischen dem Tensorprodukt und dem Produktmaß herrscht.

Remark 5.13

In den obigen Produkten können einzelnen Terme jeweils unendlich werden, hierbei benutzt man die Konvention

\[0 * a = 0\quad\forall a\in\overline{\R}.\]

Man kann zeigen, dass ein Produktmaß stets existiert siehe ??. Allerdings ist es nicht notwendigerweise eindeutig bestimmt, hierfür benötigt man die sogenannte \(\sigma\)-Endlichkeit.

Definition 5.27

Es sei \((\Omega,\Sigma,\mu)\) ein Maßraum, das Maß \(\mu\) heißt \(\sigma\)-endlich, falls eine Folge von Mengen \(A_i\in\Sigma,i\in\N\) existiert, s.d., \(\mu(A_i)<\infty\) und

\[\bigcup_{i\in\N} A_i = \Omega.\]

Remark 5.14

Das wichtigste Beispiel für uns ist das Lebesgue-Maß auf \(\R^n\) welches bezüglich der Borelschen \(\sigma\)-Algebra zwar nicht endlich aber \(\sigma\)-endlich ist. Insbesondere ist es damit auch \(\sigma\)-endlich bezüglich der Lebesgue \(\sigma\)-Algebra \(\mathcal{A}\).

Für \(\sigma\)-endliche Maße kann man zeigen, dass ein eindeutig bestimmtes Produktmaß existiert.

Theorem 5.10

Es seien \((\Omega_1,\Sigma_1,\mu_1), (\Omega_2,\Sigma_2,\mu_2)\) zwei \(\sigma\)-endliche Maßräume, dann existiert eine eindeutig bestimmtes Produktmaß

\[\mu_1\otimes \mu_2:\Sigma_1\otimes\Sigma_2\to[0,\infty],\]

s.d. die Bedingung

\[(\mu_1\otimes\mu_2)(A\times B) = \mu_1(A)\cdot\mu_2(B)\quad\forall A\in\Sigma_1, B\in\Sigma_2,\]

erfüllt ist.

Proof. See Bogachev ref missing.

Anhand von Example 5.5 haben wir gesehen, dass die Lebesgue \(\sigma\)-Algebra auf \(\R^{n+m}\) größer ist als die Produkt \(\sigma\)-Algebra. Allerdings kann man zeigen, dass das Produktmaß zumindest auf der kleineren Produktalgebra übereinstimmt.

Lemma 5.27

Es gilt

\[\lambda^{n+m} = \overline{\lambda^n\otimes\lambda^m},\]

insbesondere folgt damit für eine beliebige Menge \(E\in \mathcal{A}(\R^n)\otimes\mathcal{A}(\R^m)\)

\[\lambda^{n+m}(E) = (\lambda^n\otimes\lambda^m)(E).\]

Proof. Siehe z.B. [Bog07] Theorem 1.5.6.

Speziell für \(A_1\in\mathcal{A}(\R^n), A_2\in\mathcal{A}(\R^m)\) folgt damit

\[\lambda^{n+m}(A^1\times A^2)=\lambda^{n}(A^1)\cdot\lambda^{m}(A^2).\]

5.3.3. Das Prinzip von Cavalieri¶

Im vorherigen Abschnitt haben wir Produkte von Maßen betrachtet. Insbesondere haben wir erkannt, dass wir für Mengen der Form \(A\times B\), dass Lebesgue-Maß multiplikativ aufteilen können,

\[\lambda^{n+m}(A\times B) = \lambda^n(A)\,\lambda^m(B).\]

Unser Ziel ist es nun das Lebesgue-Maß beliebige messbare Mengen \(E\subset\R^{n+m}\) mithilfe der niedrigdimesnionaleren Lebesgue-Maße auszudrücken. Dies führt auf das sogenannte Prinzip von Cavalieri.

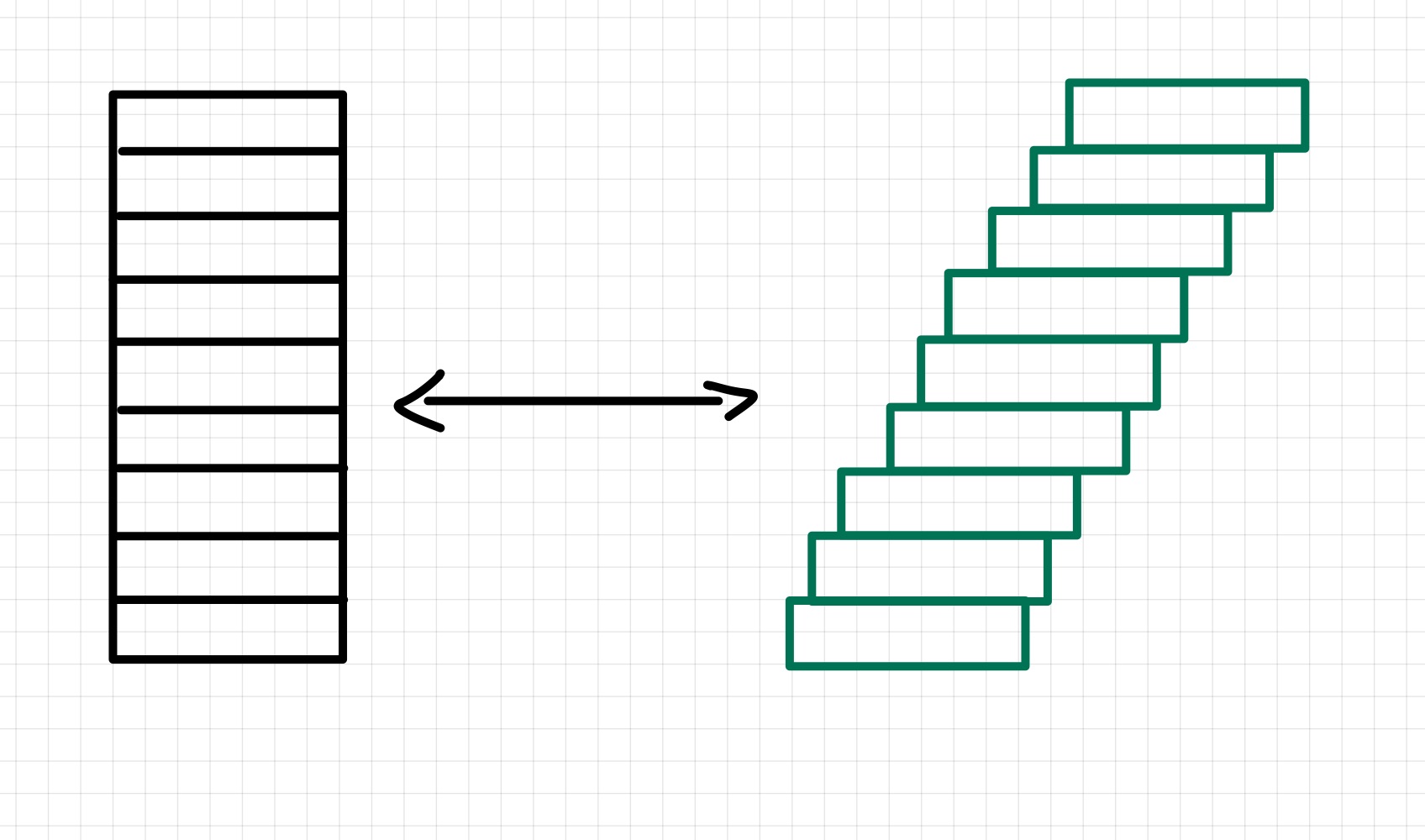
Abb. 5.6 Visualisierung für das Prinzip von Cavalieri, beide Objekte haben die gleiche Fläche.¶

Das Prinzip beruht auf der Intuition, dass zwei Körper, das gleiche Volumen haben, sofern alle ihre Schnittflächen welche parallel zu einer Grundfläche verlaufen gleich sind. Für \(\R^2\) ist dieses Prinzip in Abb. 5.6 dargestellt. Formal bedeutet das, dass wir für eine messbare Menge \(E\), den Inhalt über das Integral der Schnitte ausdrücken wollen, es gibt hier also drei Größen

\[\lambda^{n+m}(E), \int_{\R^n} \lambda^m(E_x) d\lambda^n(x), \int_{\R^m} \lambda^m(E_y) d\lambda^m(y)\]

welche wir in Beziehung zueinander setzten wollen.

Ein Konzept was man in diesem Kontext benötigt, sind sogenannte monotone Klassen.

Definition 5.28 (Monotone Klasse)

Es sei \(\Omega\) eine Menge, ein Teilmengensystem \(\mathcal{C}\subset 2^\Omega\) heißt monotone Klasse, falls

Für eine aufsteigende Folge von Mengen \(A_i\in\mathcal{C}, A_i\subset A_{i+1}, i\in\N\) gilt auch

\[\bigcup_{i\in\N} A_i\in\mathcal{C}.\]
Für eine absteigende Folge von Mengen \(A_i\in\mathcal{C}, A_i\supset A_{i+1}, i\in\N\) gilt auch

\[\bigcap_{i\in\N} A_i\in\mathcal{C}.\]

Offensichtlich ist jede \(\sigma\)-Algebra eine monotone Klasse,die Umkehrung dieser Aussage gilt nicht im Allgemeinen.

Betrachtet man analog zur kleinsten von \(\mathcal{C}\) erzeugten \(\sigma\)-Algebra die kleinste von \(\mathcal{C}\) erzeugt monotone Klasse \(\text{M}\big[\mathcal{C}\big]\) so gilt folgendes hilfreiches Lemma.

Lemma 5.28 (Monotone Klassen Lemma)

Es sei \(\mathcal{C}\) eine Mengenalgebra, dann gilt

\[\sigma(\mathcal{C}) = \text{M}\big[\mathcal{C}\big].\]

Proof. Siehe z.B. [Tao07] Lemma 1.7.14.

Remark 5.15

Für zwei \(\sigma\)-Algebren ist das kartesische Produkt \(\Sigma_1\times\Sigma_2\) i.A. keine Mengenalgebra, die Menge

\[\Sigma_1\diamond\Sigma_2:= \left\{\bigcup_{i=1}^N A^1_i\times A^2_i: A^1_i\in\Sigma_1, A^2_i\in\Sigma_2\quad i=1,\ldots,n\right\}\]

allerdings schon und sie erzeugt offensichtlich auch die Produkt-\(\sigma\)-Algebra,

\[\sigma(\Sigma_1\diamond\Sigma_2) = \Sigma_1\otimes\Sigma_2.\]

Diese Tatsache nutzen wir im Folgenden aus, um das Prinzip von Cavalieri zu zeigen.

Mithilfe des monotone Klassen Lemmas und den vorherigen Überlegungen können wir nun das Prinzip von Cavalieri beweisen.

Theorem 5.11 (Das Prinzip von Cavalieri)

Sei \(E \in \mathcal{A}(\R^n)\otimes\mathcal{A}(\R^m)\) mit \(\lambda^{n}\otimes\lambda^{m}(E) < \infty\), dann gilt für fast alle \(x\in\R^n,y\in\R^m\), dass die Schnitte \(E_x, E^y\) auch Lebesgue-messbar sind, die Funktionen

\[\begin{split}x \mapsto \lambda^m(E_x)\\ y \mapsto \lambda^n(E^y)\end{split}\]

sind messbar und es gilt

\[\begin{split}\lambda^{n}\otimes\lambda^{m}(E) &= \int_{\R^n} \lambda^m(E_x) d\lambda^n(x)\\ &= \int_{\R^m} \lambda^n(E^y) d\lambda^m(y).\end{split}\]

Proof. Es sei \(\mathcal{C}\subset\mathcal{A}(\R^n)\otimes\mathcal{A}(\R^m)\) das System aller Mengen s.d. die Aussage gilt. Dann ist \(\mathcal{C}\) eine monotone Klasse und

\[\mathcal{A}(\R^n)\diamond\mathcal{A}(\R^m)\subset \mathcal{C}.\]

Mit dem monotone Klassen Lemma (Lemma 5.28) folgt dann

\[\mathcal{A}(\R^n)\otimes\mathcal{A}(\R^m) = \sigma(\mathcal{A}(\R^n)\diamond\mathcal{A}(\R^m)) = \text{M}\big[\mathcal{A}(\R^n)\diamond\mathcal{A}(\R^m)\big] \subset \text{M}\big[\mathcal{C}\big] = \mathcal{C}.\]

Ein Korollar aus der obigen Aussage ist, dass fast alle Schnitte einer \(\lambda^n\otimes\lambda^m\) Nullmenge selbst Nullmengen bezüglich \(\lambda^n\), bzw. \(\lambda^m\) sind.

Corollary 5.2

Es sei \(E\in\mathcal{A}(\R^n)\otimes\mathcal{A}(\R^m)\) eine Nullmenge, dann folgt, dass für fast alle \(x\in\R^n,y\in\R^m\) auch \(\lambda^m(E_x)=0=\lambda^n(E^y)\) gilt.

Proof. Für die Funktion \(f:x\mapsto \lambda^m(E_x)\) gilt mit dem Prinzip von Cavalieri, dass

\[0 = \lambda^{n}\otimes\lambda^{m}(E) = \int_{\R^n} f(x)d\lambda^n(x)\]

und daher mit ??, dass

\[f(x)=\lambda^m(E_x)=0\]

für fast alle \(x\in\R^n\). Die Aussage für \(\lambda^n(E^y)\) folgt analog.

Diese Korollar erlaubt es uns die Aussage von Cavalieri auf alle Mengen \(E\in \mathcal{A}(\R^{n+m})\) zu verallgemeinern.

Lemma 5.29

Die Aussage von Theorem 5.11 (Prinzip von Cavalieri) gilt auch für Mengen \(E\in \mathcal{A}(\R^{n+m})\).

Proof. Es sei \(E\in \mathcal{A}(\R^{n+m})\), nach Lemma 5.26 existieren Mengen \(\tilde{E}\in\mathcal{A}(\R^n)\otimes\mathcal{A}(\R^m)\), \(N\subset \tilde{N}\), s.d.

\[\begin{split}E = \tilde{E}\cup N\\ (\lambda^n\otimes\lambda^m)(\tilde{N}) = 0.\end{split}\]

Insbesondere ist dann

\[E\setminus \tilde{N} = \left(\tilde{E}\setminus \tilde{N} \right)\cup \underbrace{\left(N\setminus \tilde{N}\right)}_{=\emptyset} = \tilde{E}\setminus \tilde{N}\in \in\mathcal{A}(\R^n)\otimes\mathcal{A}(\R^m)\]

daher können wir Theorem 5.11 auf \(E\setminus \tilde{N}\) anwenden. Da aber fast alle Schnitte \(\tilde{N}_x,\tilde{N}^y\) Nullmengen sind, gilt die Aussage, dann für fast alle \(x,y\in E\).

Mit dieser Aussage können wir nun ein Beispiel betrachten, in welchem wir die Fläche eines Kreises berechnen.

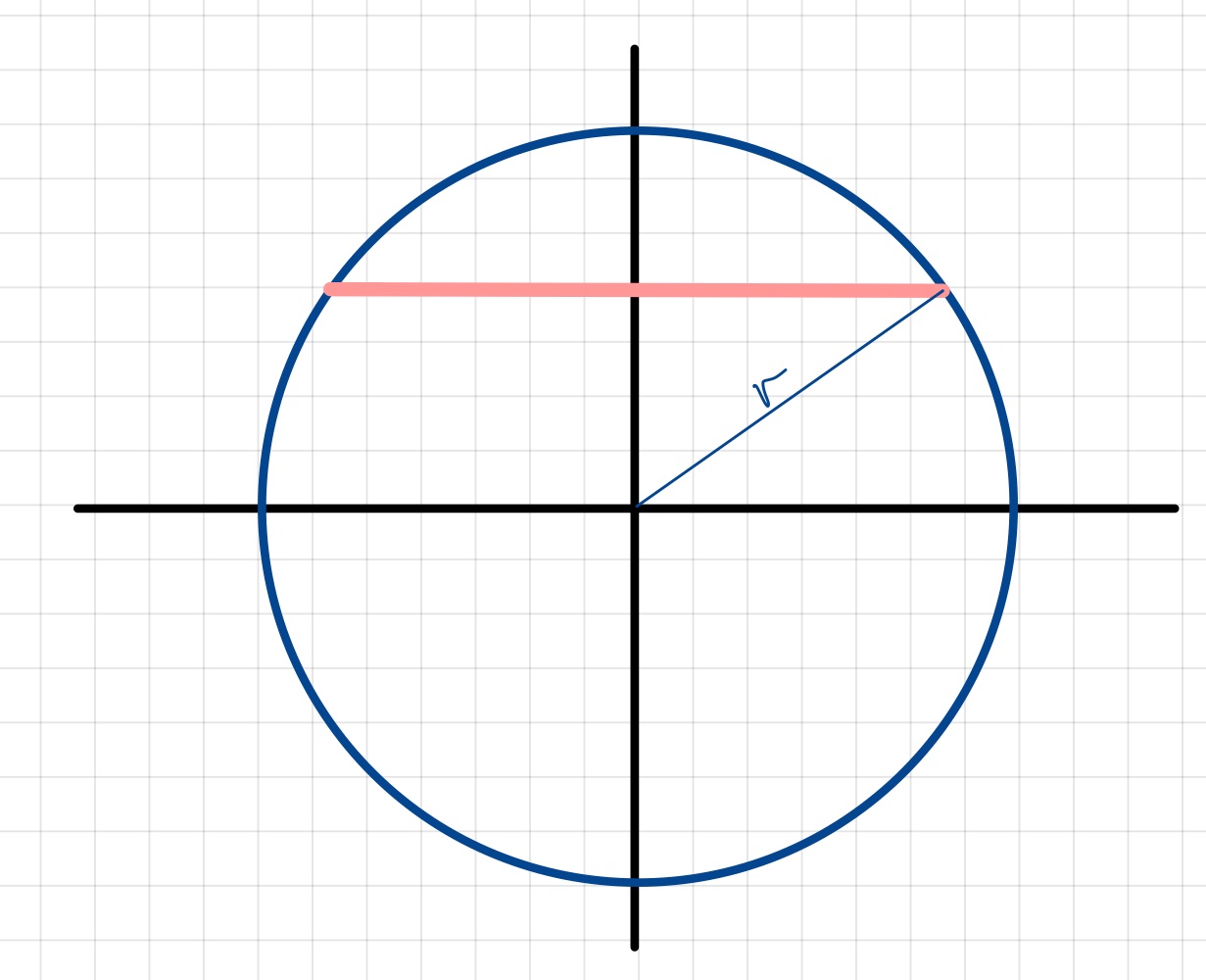
Abb. 5.7 Visualisierung für Example 5.6.¶

Example 5.6

Wir betrachten den \(2\)-dimensionale Ball

\[B_r^2:=\{x\in\R^2: |x|\leq r\},\]

wir erkennen, dass sich ein Schnitt für \(\abs{y}\leq r\) jeweils ergibt durch

\[(B_r^2)_y = \{x:(x,y)\in B_r^2\} = \{x\leq\sqrt{r^2-y^2}\} = [-\sqrt{r^2-y^2},\sqrt{r^2-y^2}]\]

und ansonsten leer ist.

Somit erhalten wir

\[\begin{split}\lambda^1((B_r^2)_y) = \begin{cases} 2 \sqrt{r^2-y^2}&\text{ falls }y\leq r\\ \emptyset\text{ sonst} \end{cases}.\end{split}\]

Damit erhalten wir mithilfe des Prinzips von Cavalieri

\[\begin{split}\lambda^2(B_r^2) &= \int_{\R} \lambda^1((B_r^2)_y) d\lambda^1(y) = \int_{[-r,r]} 2 \sqrt{r^2-y^2} d\lambda^1(y)\\ &= 2\int_{-r}^r \sqrt{r^2 - y^2} dy = \lim_{t\to r}\left[y \sqrt{r^2-y^2} +r^2\arctan\left(\frac{y}{\sqrt{r^2-y^2}}\right)\right]^t_{-t}\\ &= r^2\pi.\end{split}\]

Das Volumen einer Kugel in \(n\)-Dimensionen lässt sich mithilfe des folgenden Lemmas berechnen.

Lemma 5.30

Für die \(n\)-dimensionale Kugel

\[B_r^n:=\{x\in\R^n: |x|\leq r\}\]

gilt

\[\begin{split}\lambda^n(B_r^n) = r^n\, \begin{cases} \frac{1}{(n/2)!} \pi^{n/2}&\text{ falls }n \text{ gerade,}\\ \frac{2}{1\cdot 3\cdot\ldots n} (2\pi)^{(n-1)/2}&\text{ falls }n \text{ ungerade.} \end{cases}\end{split}\]

Proof. Siehe Hausaufgabe.

5.3.4. Der Satz von Tonelli-Fubini¶

Das Prinzip von Cavalieri erlaubt es uns nun das Maß einer Menge über ihr das Produktmaß bzw. über Integrale auszudrücken. Insbesondere gilt für Indikatorfunktionen und messbare Mengen \(E\in\mathcal{A}(\R^{n+m})\), dass

\[\int_{\R^{n+m}} \bone_E d\lambda^{n+m} = \int_{\R^{n}} \int_{\R^{m}} \bone_{E_x}(y) d\lambda^m(y)d\lambda^n(x) = \int_{\R^{m}} \int_{\R^{n}} \bone_{E_y}(x) d\lambda^m(x)d\lambda^n(y).\]

Da das Integral aber gerade über einfache Funktionen und somit über Indikatorfunktionen definiert ist, liegt die Vermutung nahe, dass die Aussage auch für beliebige messbare Funktionen \(f:\R^{n+m}\to\overline{R}\) gilt. Dieses Resultat ist als Satz von Tonelli bekannt und erlaubt uns Integrale über Funktionen mehrere Variablen durch Doppelintegrale darzustellen. Hierbei ist jedoch anumerken, dass der Satz von Tonelli nur für nicht-negative Funktionen gilt.

Theorem 5.12 (Satz von Tonelli)

Es sei \(f:\R^{n+m}\to [0,\infty]\) eine Lebesgue-messbare Funktion, dann gilt für fast alle \(x\in\R^n,y\in\R^m\), dass die Funktionen \(x\mapsto f(x,y), y\mapsto f(x,y)\) auch Lebesgue-messbar sind. Insbesondere sind auch die Funktionen

\[\begin{split}x \mapsto \int_{\R^m} f(x,y) d\lambda^m(y)\\ y \mapsto \int_{\R^n} f(x,y) d\lambda^n(x)\end{split}\]

messbar und es gilt

\[\begin{split}\int_{\R^{n+m}} f(x,y) d\lambda^{n+m}(x,y) &= \int_{\R^n}\int_{\R^m} f(x,y) d\lambda^{n}(x)d\lambda^m(y)\\ &= \int_{\R^m}\int_{\R^n} f(x,y) d\lambda^{m}(y)d\lambda^n(x).\end{split}\]

Proof. Man beweist die Aussage zunächst für Funktionen \(f:\R^{n+m}\to\overline{R}\) welche bezüglich \(\mathcal{A}(\R^n)\otimes\mathcal{A}(\R^m)\) messbar sind. Hierfür erkennt man durch mehrfache Anwendung des Satzes von Beppo Levi (Lemma 5.21) unter Ausnutzung der \(\sigma\)-Endlichkeit von \(\mathcal{A}(\R^n)\) und \(\mathcal{A}(\R^m)\), dass es reicht die Aussage auf Mengen endlichen Maßes zu zeigen. Da sich nach Lemma 5.20 aber jede Funktion durch einfache Funktionen approximieren lässt und das Integral linear ist, reicht es die Aussage für Indikatorfunktionen zu zeigen. Hier folgt die Aussage aber aus dem Prinzip von Cavalieri, Theorem 5.11.

Benutzten wir nun Corollary 5.2 so folgt die Behauptung auch für Funktionen welche bezüglich \(\mathcal{A}(\R^{n+m})\) messbar sind.

In der obigen Aussage haben wir gefordert, dass die Funktionen nicht-negativ sind. Um eine analogen Aussage auch für Funktionen mit wechselndem Vorzeichen zu erhalten müssen wir fordern, dass

\[\int_{\R^{n+m}} \abs{f(x,y)} d\lambda^{n+m}(x,y) <\infty\]

gilt. Dies ist Aussage des Satzes von Fubini.

Theorem 5.13 (Satz von Fubini)

Es sei \(f:\R^{n+m}\to \overline{\R}\) eine Lebesgue-integrierbare Funktion, dann gilt für fast alle \(x\in\R^n,y\in\R^m\), dass die Funktionen \(x\mapsto f(x,y), y\mapsto f(x,y)\) auch Lebesgue-messbar sind. Insbesondere sind auch die Funktionen

\[\begin{split}x \mapsto \int_{\R^m} f(x,y) d\lambda^m(y)\\ y \mapsto \int_{\R^n} f(x,y) d\lambda^n(x)\end{split}\]

messbar und es gilt

\[\begin{split}\int_{\R^{n+m}} f(x,y) d\lambda^{n+m}(x,y) &= \int_{\R^n}\int_{\R^m} f(x,y) d\lambda^{n}(x)d\lambda^m(y)\\ &= \int_{\R^m}\int_{\R^n} f(x,y) d\lambda^{m}(y)d\lambda^n(x).\end{split}\]

Proof. Folgt aus dem Satz von Tonelli, Theorem 5.12.

5.3.5. Die Jacobische Transformationsformel¶

Die Intuition hinter dem Prinzip von Cavalieri ist, dass man über parallele Schnitte integriert und erkennt, dass das Volumen so erhalten bleibt. Wir fragen uns nun, wie sich das Volumen verhält, wenn man zwei Mengen vergleicht deren parallele Schnitte nicht unbedingt gleich sind, aber welche über eine Abbildung ineinander überführbar sind.

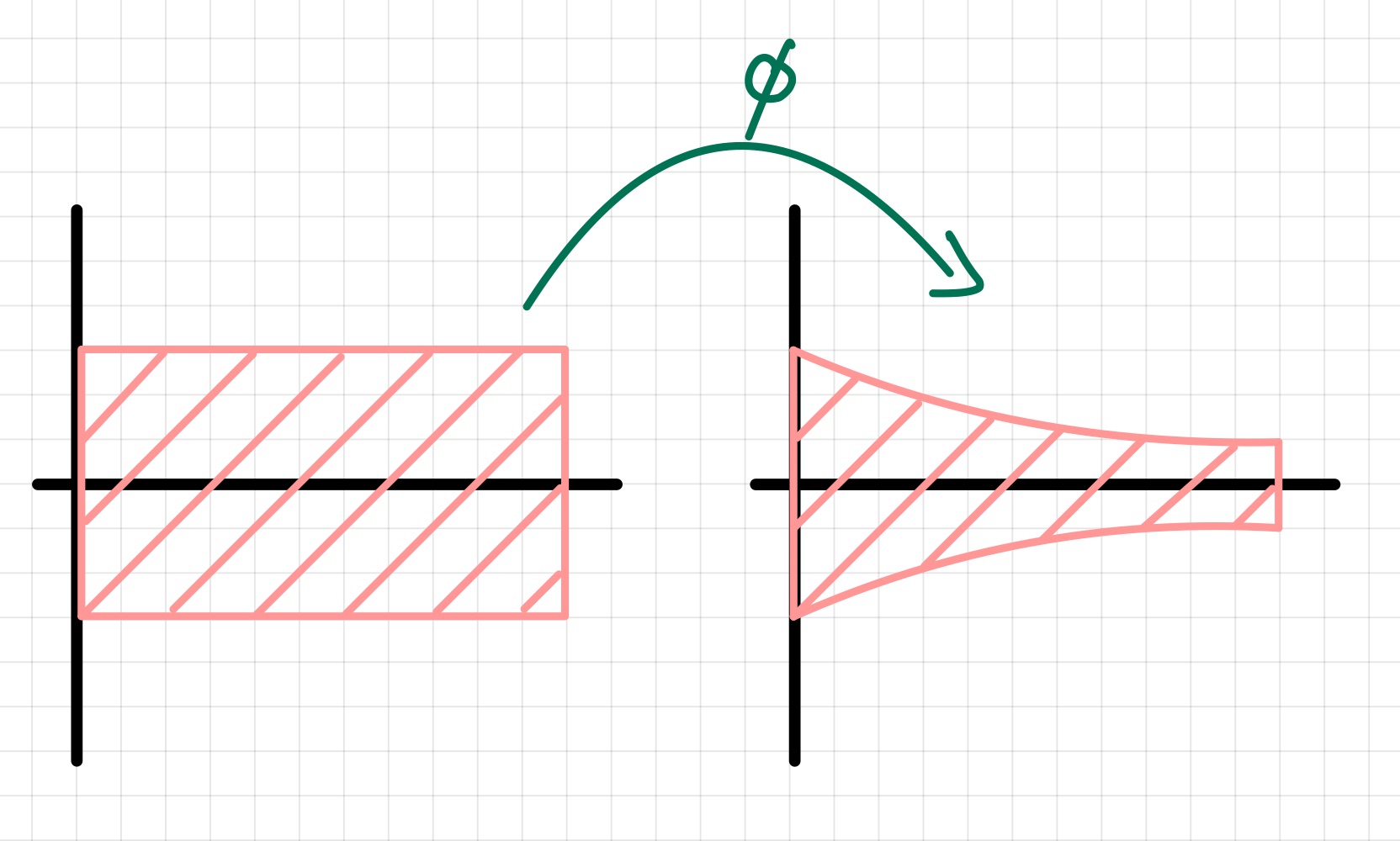
Abb. 5.8 Visualisierung von Mengentransformationen.¶

In Remark 5.6 haben wir für eine Matrix \(M\) und eine Lebesgue-messbare Menge \(A\) bereits die Identität

\[\lambda(MA) = |\det(M)| \, \lambda(A)\]

kennengelernt. Wir verllgemeinern diese Aussage nun, indem wir beliebige \(C^1\)-Diffeomorphismen betrachten.

Theorem 5.14 (Jacobische Transformationsformel)

Seien \(U, V \subset \R^n\) offene Teilmengen und die Abbildung

\[\Phi \colon U \rightarrow V := \Phi(U)\]

sei ein \(C^1\)-Diffeomorphismus, d.h., dass die Abbildung \(\Phi\) invertierbar ist, und dass sowohl \(\Phi\) als auch die Umkehrabbildung \(\Phi^{-1}\) stetig differenzierbar sind. Sei außerdem \(f \colon V \rightarrow \R\) eine Lebesgue-integrierbare Funktion.

Dann gilt, dass die Verknüpfung \(f \circ \Phi \colon U \rightarrow \R\) auch Lebesgue-integrierbar ist und es gilt die folgende Integrationsregel

\[\int_{\Phi(U)} f(y)\,d\lambda^n(y) = \int_U (f \circ \Phi)(x) \cdot \abs{\det(D\Phi(x))} d\lambda^n(x). \]

Hierbei ist man \(\det(D\Phi(x))\) die Jacobi-Determinante.

Proof. Siehe z.B. [Bog07] Theorem 3.7.1.

Remark 5.16

Für \(n=1\) ist diese Regel schon als Substitutionsregel bekannt.

Example 5.7

ToDo

Mathematik für Physikstudierende C

Integrationstechniken

Inhalt