5.2. Lebesgue-Integral¶

Anhand des in Das Lebesgue Maß konstruierten Maßes wollen wir nun einen neuen Begriff des Integrals herleiten. Unsere Motivation hierbei war anstatt den Definitionsbereich, den Bildbereich einer Funktion \(f:\Omega\to\R\) zu zerteilen. Dies führt auf das Problem, dass man Urbildern

\[f^{-1}(I)\]

für Mengen \(I\subset\R\) ein Maß zuordnen muss. Dies soll im Folgenden mithilfe des Lebesgue-Maßes geschehen. Um \(f^{-1}(I)\) allerdings im Lebesgue-Maß auswerten zu können, müssen wir voraussetzen, dass diese Menge messbar ist, was zu speziellen Anforderungen an die Funktion \(f\) führt, welche wir im nächsten Abschnitt behandeln.

5.2.1. Messbare Funktionen¶

Wir beginnen mit der Definition von messbaren Funktionen. Wir benutzen hierbei den Begriff eines Messraums der anders als ein Maßraum nur eine Grundmenge und eine \(\sigma\)-Algebra voraussetzt und kein Maß beinhaltet.

Definition 5.19 (Messbarkeit von Funktionen)

Es seien \((\Omega_1,\Sigma_1), (\Omega_1,\Sigma_1)\) zwei Messräume und \(f:\Omega_1\to\Omega_2\) eine Funktion, dann nennen wir \(f\) messbar, falls

\[f^{-1}(A)\in\Sigma_1\quad\forall A\in\Sigma_2\]

Für ein Teilmengensystem \(\mathcal{C}\subset 2^{\Omega_2}\) benutzten wir auch die Schreibweise

\[f^{-1}(\mathcal{C}) = \{ f^{-1}(C): C\in\mathcal{C}\},\]

womit sich die Messbarkeit einer Funktion äquivalent auch durch die Bedingung

\[f^{-1}(\Sigma_2)\subset\Sigma_1\]

schreiben lässt. In diesem Kapitel wollen wir speziell Funktionen \(f:\Omega\to\overline{\R}\) betrachten wobei \(\Omega\subset\R^n\).

Definition 5.20

Wir nennen eine Funktion \(f:\R^n\to\overline{\R}\) Borel-messbar, falls

\[f^{-1}(\mathcal{B}(\overline{\R}))\subset \mathcal{B}(\R^n).\]

Analog nennen wir \(f\) Lebesgue-messbar, falls

\[f^{-1}(\mathcal{B}(\overline{\R}))\subset \mathcal{A}(\R^n).\]

Eine wichtige Aussage in dem Kontext von messbaren Funktionen ist die Tatsache, dass sich Urbild mit dem \(\sigma\)-Operator vertauschen lässt, wobei für \(\mathcal{C}\subset 2^\Omega\) die Menge \(\sigma(\mathcal{C})\) gerade die kleinste \(\sigma\)-Algebra ist welche \(\mathcal{C}\) enthält siehe Abschnitt 5.1.1.

Lemma 5.14

Es sei \(f:\Omega_1\to\Omega_2\) eine Funktion und \(\mathcal{C}\subset 2^{\Omega_2}\) ein Teilmengensystem, dann gilt

\[f^{-1}(\sigma(\mathcal{C})) = \sigma(f^{-1}(\mathcal{C})).\]

Proof. ToDo Vorlesung ab 29:52.

Mit diesem Lemma können wir die folgenden Aussagen zeigen.

Lemma 5.15

Borel-messbare Funktionen sind Lebesgue-messbar
Stetige Funktionen sind Borel-messbar.

Proof. ToDo Vorlesung ab 17:12

5.2.2. Charakterisierung über Niveaumengen¶

Im Falle von Borel und Lebesgue-Messbarkeit haben wir als Zielalgebra \(\B(\overline{\R})\) betrachtet. Dank der Charakterisierung der Topologie über Intervalle hat man die Möglichkeit statt aller messbarer Mengen nur Niveaumengen einer Funktion zu betrachten. Dies führt auf das folgende sehr praktische Lemma.

Lemma 5.16

Es sei \((\Omega,\Sigma)\) ein Messraum, eine Funktion \(f:\Omega\to\overline{\R}\) eine Funktion ist genau dann messbar bezüglich \(\Sigma\), falls für die Niveaumengen gilt

\[\{f< c\}\in\Sigma\quad\forall c\in\R.\]

Proof. Wir betrachten das Mengensystem

\[\mathcal{C}:=\{[-\infty,c):c\in\R\}\]

und erkennen, dass

\[f^{-1}(\mathcal{C}) = \{\{f<c\}:c\in\R\}.\]

Weiterhin gilt wegen Lemma 5.5 und Lemma 5.14, dass

\[\sigma(f^{-1}(\mathcal{C})) = f^{-1}(\sigma(\mathcal{C})) = f^{-1}(\B(\overline{\R}))\]

und daher ist Messbarkeit bezüglich \(\Sigma\) äquivalent zu

\[\sigma(f^{-1}(\mathcal{C})) \subset \Sigma\]

was aber wiederum äquivalent zu

\[f^{-1}(\mathcal{C}) \subset \Sigma\]

ist.

Remark 5.9

Für uns ist vor allem der Fall von Bedeutung, wenn \(\Sigma\) im obigen Lemma die Borel \(\sigma\)-Algebra oder die Lebesgue \(\sigma\)-Algebra auf \(\R^n\) ist. Da wir aber keine speziellen Eigenschaften dieser \(\sigma\)-Algebren ausnutzen und lediglich die Tatsache ausnutzen, dass die Zielalgebra \(\B(\overline{\R})\) ist, ist es leichter die Aussagen mit allgemeinem \(\Sigma\) zu formulieren.

Mithilfe dieses Lemma können wir die folgende Aussage zeigen.

Lemma 5.17

Es sei \((\Omega,\Sigma)\) ein Messraum und \(f,g:\Omega\to\overline{\R}\) zwei bezüglich \(\Sigma\) messbare Funktionen, dann gilt

\(f+g\) ist messbar,
\(\lambda f\) ist messbar für alle \(\lambda\in\overline{\R}\),
\(f\cdot g\) ist messbar,
falls \(g\neq 0\) ist \(f/g\) messbar,
\(\max\{f,g\}, \min\{f,g\}\) sind messbar

bezüglich \(\Sigma\).

Proof. Siehe Übung.

Für Folgen von messbaren Funktionen gilt auch, dass deren Grenzwerte messbar sind.

Lemma 5.18

Es sei \((\Omega,\Sigma)\) ein Messraum, \(f_n \colon \Omega\to\overline{\R},n\in\N\) eine Folge von bezüglich \(\Sigma\) messbaren Funktionen, dann sind

\(\inf_{n\in\N} f_n\) und \(\sup_{n\in\N} f_n\),
\(\liminf_{n\to\infty} f_n\) und \(\limsup{n\to\infty} (f_n)\)

auch messbar bezüglich \(\Sigma\).

Proof. ToDo, siehe Vorlesung Minute 80:30.

5.2.3. Das Lebesgue-Integral einfacher Funktionen¶

Für das Riemann-Integral werden Treppenfunktionen benutzt, welche auf einem diskretisierten Definitionsbereich definiert sind. Als Analogon betrachtet man hier sogenannte einfache Funktionen, welche mithilfe der Indikatorfunktionen

\[\begin{split}\bone_A(x):= \begin{cases} 1&\text{ falls }x\in A,\\ 0&\text{ sonst,} \end{cases}\end{split}\]

für verschiedenen Mengen \(A\subset \R^n\) definiert sind.

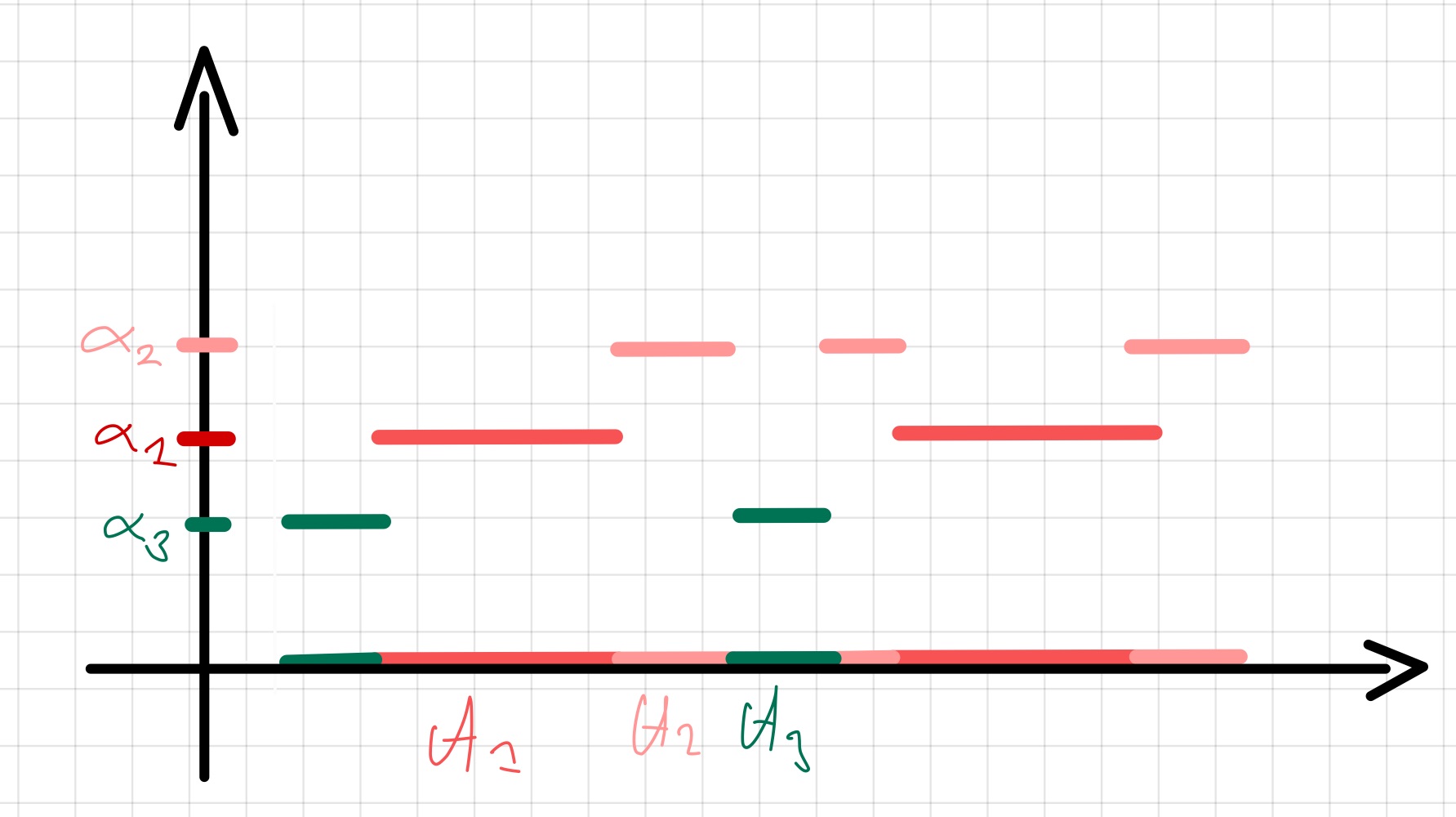
Abb. 5.4 Visualisierung einer einfachen Funktion.¶

Definition 5.21

Eine Funktion \(f:\R^n\to\overline{\R}\) heißt einfach, falls Koeffizienten \(\alpha_i\in\overline{\R}\) und messbare Mengen \(A_i\in\mathcal{A}(\R^n)\) für \(i=1,\ldots,N\) existieren, s.d.,

\[f = \sum_{i=1}^N \alpha_i \bone_{A_i}.\]

Man erhält über die Definition direkt ein Lemma, dass einfache Funktionen Lebesgue-messbar sind.

Lemma 5.19

Es sei \(f:\R^n\to\overline{\R}\) eine einfache Funktion, dann ist \(f\) Lebesgue-messbar.

Proof. Siehe Vorlesung ab Minute 8:45.

Für einfache Funktionen können wir analog zum Riemann-Integral das Lebesgue-Integral definieren, indem wir das Maß der einzelnen Mengen multipliziert mit den Funktionswerten summieren, welche eine einfache Funktion erzeugen.

Remark 5.10 (Wohldefiniertheit)

Es ist wichtig anzumerken, dass für eine einfache Funktion \(f\) verschiedene Zerlegungen in Mengen \(A_i\) und Koeffizienten \(\alpha_i\) existieren. Allerdings erkennen wir, dass der Wert des Integrals unabhängig von der Wahl der Zerlegung ist und das Intergal somit wohldefiniert ist.

5.2.4. Das Lebesgue-Integral nicht-negativer Funktionen¶

Die wichtige Eigenschaft, welche die Betrachtung von einfachen Funktion so relevant macht, ist dass sich messbare Funktionen beliebig gut durch einfache Funktionen approximieren lassen. Diese Tatsache formulieren wir in folgendem Lemma.

Lemma 5.20

Sei \(f \colon \Omega \to [0,\infty]\) eine Lebesgue-messbare Funktion, dann existiert eine monoton wachsende Folge \((f_i)_{i_\in N}\) von einfachen Funktionen mit

\[\begin{split}f_i&\leq f_{i+1}\\ f_i &= 0\text{ in }\Omega^C\\ f&=\lim_{i\to\infty} f_i.\end{split}\]

Proof. Siehe Vorlesung ab Minute 13:00.

Mithilfe der Tatsache, dass sich messbare Funktionen beliebig gut durch einfache Funktionen approximieren lassen, können wir nun das Lebesgue-Integral für nicht-negative messbare Funktionen einführen.

Definition 5.22 (Lebesgue-Integral nicht-negativer Funktionen)

Es sei \(f:\Omega\to[0,\infty]\) Lebesgue-messbar und nach Lemma 5.20 \((f_i)_{i\in\N}\) eine monoton wachsende Folge von einfachen Funktionen mit \(\lim_{i\to\infty} f_i = f\), dann ist das Lebesgue-Integral von \(f\) definiert durch

\[\int_{\Omega} f \,d\lambda^n = \lim_{i\rightarrow \infty} \int_{\R^n} f_i \,d\lambda^n.\]

Wir zeigen im Folgenden wichtige Eigenschaften des Lebesgue-Integrals.

Theorem 5.8 (Eigenschaften des Lebesgue-Integrals)

Das Lebesgue-Integral ist wohldefiniert, d.h., sein Wert ist unabhängig von der gewählten Folge von einfachen Funktionen \((f_n)_{n\in\N}\). Darüber hinaus ist das Lebesgue-Integral linear und monoton, d.h., für nicht-negative, Lebesgue-messbare Funktionen \(f,g \geq 0,\alpha\in\overline{\R}\) gilt

\[\begin{split}\int_\Omega f+\alpha\,g\,d\lambda^n = \int_\Omega f\,d\lambda^n + \alpha\, \int_\Omega g d\lambda^n\\ f \leq g \quad \Rightarrow \quad \int_\Omega f\, d\lambda^n \leq \int_\Omega g\, d\lambda^n.\end{split}\]

Proof. Siehe Vorlesung ab Minute 30:00.

Anstatt der Folge von einfachen Funktionen, kann man auch eine beliebige monotone Folge von messbaren Funktionen benutzen um das Integral zu approximieren. Diese Aussage ist unter dem Satz von der monotonen Konvergenz oder dem Konvergenzsatz von Beppo Levi bekannt.

Lemma 5.21 (Satz von Beppo Levi)

Es sei \(f_i:\R^n\to[0,\infty],i\in\N\) eine Folge nicht-negativer Lebesgue-messbarer Funktionen mit

\[\begin{split}f_i\leq f_{i+1}\qquad\text{(Monotonie))},\\ \lim_{i\to\infty} f_i = f\qquad\text{(Konvergenz)},\end{split}\]

wobei \(f:[0,\infty]\to\overline{\R}\) auch Lebesgue-messbar ist, dann gilt

\[\lim_{i\to\infty} \int_{\R^n} f_i \,d\lambda^n = \int_{\R^n} f \,d\lambda^n\]

Proof. Ref missing.

Eine weitere Aussage in diesem Kontext ist das Lemma von Fatou, welches eine Abschätzung für eine nicht notwendigerweise konvergierende Folge von Funktionen zeigt.

Lemma 5.22 (Lemma von Fatou)

Es sei \(f_i:\R^n\to[0,\infty],i\in\N\) eine Folge nicht-negativer Lebesgue-messbarer Funktion, dann ist

\[f(x) := \liminf_{i\to\infty} f_i(x)\]

nicht-negativ und Lebesgue-messbar und es gilt

\[\liminf_{i\to\infty} \int_{\R} f_i\, d\lambda^n \geq \int_\R^n f\, d\lambda^n.\]

Proof. Ref missing.

5.2.5. Das Lebesgue-Integral integrierbarer Funktionen¶

Wir wollen nun das Lebesgue-Integral auf messbaren Funktionen mit wechselndem Vorzeichen betrachten. Dafür spalten wir eine Funktionen in ihren positiven und ihren negativen Teil auf und bilden das Integral über diese Funktionen. Um die beiden Teile aufsummieren zu können, müssen wir allerdings fordern, dass beide endlich sind.

Definition 5.23 (Lebesgue-Integral integrierbarer Funktionen)

Sei \(f \colon \R^n \rightarrow \R\) eine Lebesgue-messbare Funktion, wir nennen die Funktion \(f\) Lebesgue-integrierbar, falls

\[\int_{\R^n} \abs{f} d\lambda^n < +\infty\]

gilt. Für eine Lebesgue-integrierbare Funktion \(f\), definieren wir entsprechende positive integrierbare Funktionen

\[f^+ := \max \lbrace f, 0 \rbrace, \qquad f_- := \max{-f, 0},\]

so dass gilt \(f = f^+ - f_-\). Dann können wir das Lebesgue-Integral von \(f\) definieren als

\[\int_{\R^n} f\, d\lambda^n := \int_{\R^n} f^+\, d\lambda^n - \int_{\R^n} f_-\, d\lambda^n.\]

Lemma 5.23

Das Lebesgue-Integral ist ein linearer und monotoner Operator auf der Menge der Lebesgue-integrierbaren Funktionen.

Proof. ToDo

Auch für integrierbare Funktionen gibt es einen wichtigen Konvergenzsatz, der Konvergenzsatz von Lebesgue oder auch der Satz von der dominierten Konvergenz.

Theorem 5.9

Es sei \(f_i:\R^n\to\R\) eine Folge Lebesgue-messbarer Funktionen mit \(\lim_{i\to\infty} f_i =f\) und \(\abs{f}\leq g\) wobei \(g\) eine Lebesgue-integrierbare Funktion ist, dann gilt \(f\) ist Lebesgue-integrierbar und

\[\lim_{i\to\infty} \int_{\R^n} f_i\, d\lambda^n = \int_{\R^n} f\, d\lambda^n.\]

Proof. Ref missing.

5.2.6. Fast überall Eigenschaften¶

Definition 5.24

Seien \(f,g \colon \R^n \rightarrow \overline{\R}\) Lebesgue-messbare Funktionen. Wir sagen \(f = g\) fast sicher bezüglich des Lebesgue-Maßes genau dann, wenn eine Lebesgue-Nullmenge \(N\) existiert, so dass gilt

\[f(x) = g(x) \quad \forall x \in \R^n \setminus N.\]

Mathematik für Physikstudierende C

Lebesgue-Integral

Inhalt

5.2. Lebesgue-Integral¶

5.2.1. Messbare Funktionen¶

5.2.2. Charakterisierung über Niveaumengen¶

5.2.3. Das Lebesgue-Integral einfacher Funktionen¶

5.2.4. Das Lebesgue-Integral nicht-negativer Funktionen¶

5.2.5. Das Lebesgue-Integral integrierbarer Funktionen¶

5.2.6. Fast überall Eigenschaften¶