7.3. Wegintegrale¶

Der vorhergehende Abschnitt beschäftigt sich mit der komplexen Ableitung. Darauf aufbauend wollen wir in diesem Abschnitt einen Integralbegriff für komplexe Funktionen entwickeln. Für Funktionen \(f:\C\to\C\) entsteht hierbei die Schwierigkeit durch den komplexen Definitionsbereich. Für Funktionen \(g:[a,b]\to\C\) wobei \([a,b]\subset\R\) ein reelles Intervall ist können wir mithilfe des Riemann-Integrals folgendes Integral definieren.

Definition 7.3

Es seien \(a<b\) zwei reelle Zahlen und \(g:[a,b]\to\C\) eine stetige Funktion, dann definieren wir das Integral

\[\int_a^b g(t)\, dt = \int_a^b \Re(g)(t)\,dt + i\int_a^b \Im(g)(t)\, dt.\]

Wir versuchen also im Folgenden einen ähnlichen Integrationsbegriff für Funktionen \(f:\C\to\C\) zu erhalten.

7.3.1. Integration über stetig differenzierbare Wege¶

Wir beginnen diesen Abschnitt mit der grundlegenden Definition von Wegen und Kurven, welche die Grundlage der komplexen Integration bilden.

Definition 7.4 (Weg und Kurve)

Für zwei reelle Zahlen \(a<b\) betrachten wir eine Abbildung \(\gamma:[a,b]\to\C\).

Falls die Abbildung stetig ist, so nennen wir \(\gamma\) Weg mit Anfangspunkt \(\gamma(a)\) und Endpunkt \(\gamma(b)\).
Ein Weg heißt geschlossen, falls \(\gamma(a)=\gamma(b)\).
Ein Weg heißt stetig differenzierbar, falls \(\gamma^\prime\) existiert und stetig ist.

Remark 7.3

Wir beachten, dass wir bei der Definition der Differenzierbarkeit eines Weges den klassischen Begriff der Differenzierbarkeit benutzten und nicht den der Holomorphie, da der Definitionsbereich von \(\gamma:[a,b]\to\C\) rein reell ist.

Damit können wir nun das Wegintegral definieren.

Definition 7.5

Es sei \(U\subset\C\) eine offene Teilmenge und \(f:U\to\C\) eine stetige Funktion, für einen stetig differenzierbaren Weg \(\gamma:[a,b]\to\C\) definieren wir das Wegintegral

\[\int_\gamma f(z)\, dz := \int_a^b f(\gamma(t))\gamma^\prime(t)dt.\]

Ist \(\gamma\) geschlossen so schreiben wir

\[\oint_\gamma f(z)\, dz:=\int_\gamma f(z)\, dz.\]

Remark 7.4

Wir erkennen in der Definition des Wegintegrals konzeptionelle Ähnlichkeiten zur Transformationsregel Theorem 5.14.

7.3.2. Integration über stückweise differenzierbare Wege¶

Wir wollen nicht nur Wege \(\gamma:[a,b]\to\C\) betrachten welche auf dem ganzen Intervall \([a,b]\) stetig differenzierbar sein sondern wollen auch stetige Abbildungen mit endliche vielen Knickstellen zulassen.

Definition 7.6

Für zwei reelle Zahlen \(a<b\) sei \(\gamma:[a,b]\to\C\) ein Weg.

1. Falls endlich viele Punkte \(a=t_0<t_1<\ldots t_N =b\) existieren s.d. \(\gamma\rvert_{[t_j,t_{j+1}]}\) stetig differenzierbar ist, für alle \(j=0,\ldots, N-1\), so heißt \(\gamma\) Integrationsweg mit Zerlegung \((t_0,\ldots,t_N)\).

2. Falls endlich viele Punkte \(a=t_0<t_1<\ldots < t_N =b\) existieren, s.d. für alle \(j=0,\ldots, N-1\) gilt

\[\gamma(t) = \gamma(t_j) + \frac{t - t_j}{t_{j+1} - t_j} \big(\gamma(t_{j+1}) - \gamma(t_j))\quad\text{ für } t\in(t_j,t_{j+1}\big)\]

so heißt \(\gamma\) Polygonzug mit Zerlegung \((t_0,\ldots,t_N)\).

3. Falls \(\gamma\) ein Polygonzug mit Zerlegung \((t_0,\ldots,t_N)\) ist und falls für alle \(j=0,\ldots,N-1\) gilt

\[\big(\gamma(t_{j+1}) - \gamma(t_j)) \in \{ \alpha_j, \alpha_j i\}\]

für reelle Faktoren \(\alpha_j\in\R\), so heißt \(\gamma\) Treppenzug.

Remark 7.5

Jeder Polygonzug ist ein Integrationsweg.

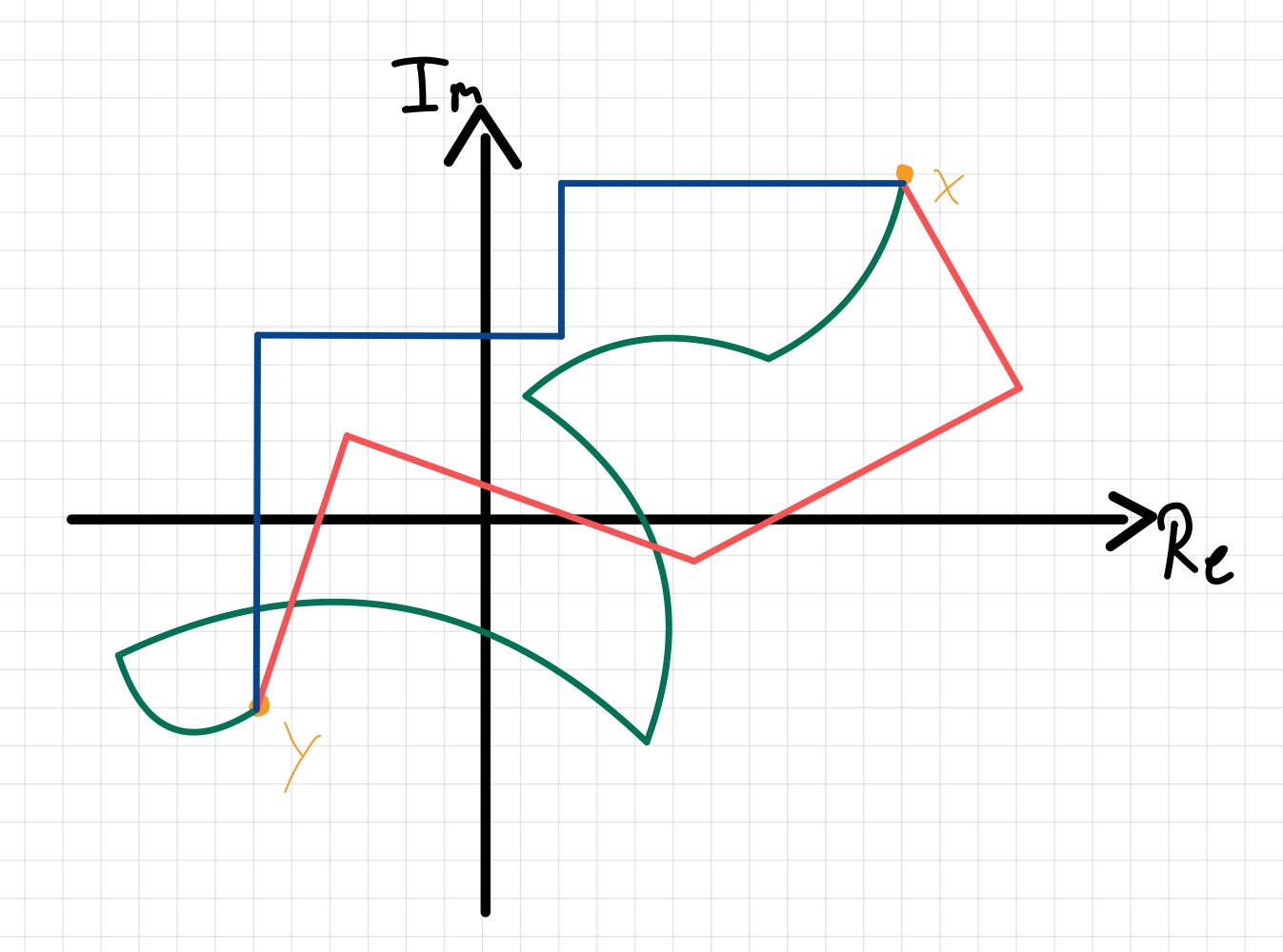
Abb. 7.1 Visualisierung eines Integrationswegs in grün, eines Polygonzugs in rot und eines Treppenzugs in blau.¶

Analog definiert man hier den Begriff des Integrals.

Definition 7.7

Es sei \(U\subset\C\) eine offene Teilmenge und \(f:U\to\C\) eine stetige Funktion, für einen Integrationsweg \(\gamma:[a,b]\to\C\) mit Zerlegung \((t_0,\ldots,t_N)\) definieren wir das Wegintegral

\[\int_\gamma f(z)\, dz:= \sum_{j=0}^{N-1} \int_{\gamma\rvert_{[t_j,t_{j+1}]}} f(z)\,dz.\]

Remark 7.6

Für einen Weg \(\gamma\) können verschiedene Zerlegungen \((t_0,\ldots,t_N)\) s.d., \(\gamma\) ein Integrationsweg bezüglich dieser Zerlegung ist. Man erkennt aber leicht, dass de Wert des Wegintegrals unabhängig von der Wahl der Zerlegung ist

Die Definition des Wegintegral ist unabhängig von Umparametrisierungen eines Weges, dies ist Inhalt des folgenden Lemmas.

Lemma 7.4

Es sei \(U\subset\C\) offen, \(\gamma:[a,b]\to U\) ein stetig differenzierbarer Weg und \(\phi:[c,d]\to[a,b]\) eine stetig differenzierbare Abbildung mit \(\phi(c)=a,\phi(d)=b\). Ist \(f:U\to\C\) stetig, so gilt

\[\int_{\gamma\circ\phi} f(z)\, dz = \int_\gamma f(z)\, dz.\]

Proof. ToDo.

Insbesondere rechtfertigt diese Aussage, dass wir für den Strahl

\[[p,q]:=\{z\in\C: z = p+t(q-p), 0\leq t\leq 1\}\]

setzten

\[\int_{[p,q]} f(z)\, dz = \int_0^1 f(p+t(q-p))\cdot (q-p)\, dt.\]

7.3.3. Stammfunktionen¶

Analog zum Begriff einer Stammfunktion in \(\R\) betrachten wir dieses Konzept nun für Funktionen \(f\C\to\C\).

Definition 7.8

Es sei \(U\subset\C\) offen, eine holomorphe Funktion \(F:U\to\C\) heißt Stammfunktion einer Funktion \(f:U\to\C\), falls

\[F^\prime = f.\]

Remark 7.7

Wir beachten, dass in der obigen Definition die komplexe Ableitung benutzt wird.

Für reelle Funktionen schafft der Hauptsatz der Differentiations- und Integrationsrechnung (HDI) einen Zusammenhang zwischen dem Integral der Ableitung und der Stammfunktion. Mithilfe des Wegintegrals wollen wir nun ein ähnliches Konzept erarbeiten und bemerken zunächst folgende Tatsache.

Lemma 7.5 (Integral einer Ableitung)

Es sei \(U\subset\C\) offen und \(f:U\to\C\) sei eine holomorphe Funktion, dann gilt

\[\int_\gamma f^\prime(z)\, dz= f(\gamma(b)) - f(\gamma(a))\]

für jeden Integrationsweg \(\gamma:[a,b]\to U\).

Proof. Sei \(\gamma:[a,b]\to\C\) zunächst stetig differenzierbar, dann gilt

\[\int_\gamma f^\prime(z)\, dz = \int_a^b f^\prime(\gamma(t))\gamma^\prime(t)\, dt =(\#).\]

Die Abbildung \((f\circ \gamma):[a,b]\to\C\) ist reell differenzierbar und mit der Kettenregel auf \(\R\) gilt

\[(f\circ\gamma)^\prime = (f^\prime\circ\gamma)\cdot\gamma.\]

Daher folgt

\[(\#) = \int_a^b (f\circ \gamma)^\prime(t)\, dt.\]

Nach dem Hauptsatz der Integrations und Differentialrechnung für reelle Funktionen folgt dann

\[(\#) = f(\gamma(b)) - f(\gamma(a)). \]

Anstatt allgemeiner offener Teilmengen \(U\subset\C\) zu betrachten schränkt man sich oft auf Gebiete ein.

Definition 7.9

Eine offenen Menge \(U\subset\C\) heißt Gebiet, falls sie zusammenhängend ist, das heißt für zwei in \(U\) offene Mengen \(A,B\subset U,A\neq\emptyset\neq B\) gilt

\[\big[A\cup B = U\big] \Rightarrow A\cap B \neq \emptyset.\]

Für Gebiete gibt es folgende hilfreiche Charakterisierungen.

Lemma 7.6

Eine Menge \(U\subset\C\) ist genau dann ein Gebiet, falls eine der folgenden Bedingungen gilt.

Die Menge \(U\) ist wegzusammenhängend, d.h., für \(x,y\in U\) existiert stets ein Weg \(\gamma:[a,b]\to U\) mit \(\gamma(a)=x,\gamma(b)=y\).
Die Menge \(U\) ist polygonzusammenhängend, d.h., für \(x,y\in U\) existiert ein Polygonzug \(\gamma:[a,b]\to U\) mit \(\gamma(a)=x,\gamma(b)=y\).
Die Menge \(U\) ist treppenzusammenhängend, d.h., für \(x,y\in U\) existiert ein Treppenzug \(\gamma:[a,b]\to U\) mit \(\gamma(a)=x,\gamma(b)=y\).

Proof. Siehe z.B. [Nee17] Lemma 3.12.

Auf Gebieten können wir mithilfe von Lemma 7.5 folgende Aussage zeigen.

Lemma 7.7

Es sei \(U\subset\C\) ein Gebiet, eine Funktion \(f:U\to\C\) ist genau dann konstant wenn \(f^\prime=0\) gilt.

Proof. Falls \(f\) konstant ist folgt per Definition \(f^\prime=0\). Ist umgekehrt \(f^\prime=0\) dann finden wir für beliebige \(x,y\in U\) einen Polygonzug \(\gamma:[a,b]\to U, \gamma(a)=x,\gamma(b)=y\) mit Zerlegung \((t_0,\ldots,t_N)\), da \(U\) ein Gebiet ist. Dieser Weg ist insbesondere ein Inetgrationsweg und mit Lemma 7.5 folgt dann

\[f(x) - f(y) = \int_\gamma f^\prime(z)\, dz = 0.\]

Da \(x,y\in U\) beliebig waren ist \(f\) konstant.

Im Folgenden formulieren wir ein zentrales Resultat für Stammfunktionen holomorpher Funktionen.

Theorem 7.2 (Existenz von Stammfunktionen)

Es sei \(U\subset\C\) offen, dann besitzt eine stetige Funktion genau dann eine Stammfunktion, falls

\[\oint_\gamma f(z)\, dz =0\]

für jeden geschlossenen Integrationsweg \(\gamma\) gilt.

Fixieren wir einen Punkt \(p\in\C\) und ist zusätzlich \(U\) zusammenhängend, so ist eine Stammfunktionen \(F:U\to\C, F(p)=c\in\C\) gegeben durch

\[F(w):= c+ \int_{\gamma_w} f(z) \,dz\]

wobei \(\gamma_w\) ein beliebiger Integrationsweg von \(p\) nach \(w\) ist.

Proof. Siehe z.B. [Nee17] Satz 3.17.

Die Bedingung an \(f\), dass alle Wegintegrale über geschlossene Wege wegfallen ist in der Praxis schwer nachzuprüfen. Für holomorphe Funktionen hat man allerdings folgendes praktische Korollar.

Corollary 7.1

Sei \(f:B_r(p)\to\C\) eine holomorphe Funktion auf der komplexen Scheibe \(B_r(p)\subset\C\) um \(p\) mit Radius \(r>0\), dann besitzt \(f\) eine Stammfunktion.

7.3.4. Integration über nicht differenzierbare Wege¶

Mithilfe des Konzepts der Stammfunktion können wir nun das Integral über beliebige Wege definieren.

Definition 7.10

Es sei \(\gamma:[a,b]\to U\) ein Weg, eine Zerlegung \((a=t_0,\ldots, t_N=b), t_j<t_{j+1}\) heißt zulässig, falls offenen Scheiben \(B^j\subset U\) existieren, s.d.

\[\gamma([t_j,t_{j+1}])\subset B^j\quad j=0,\ldots,N-1.\]

Für eine holomorphe Funktion \(f:U\to\C\) wissen wir dann, dass für einen Weg \(\gamma\) mit zulässiger Zerlegung \((t_0,\ldots,t_N)\) auf jeder Kreisscheibe \(B^j\subset U\) eine Stammfunktion \(F_j\) existiert, s.d.,

\[\int_\gamma f(z)\, dz= \sum_{j=0}^{N-1} \int_{\gamma\rvert_[t_j,t_{j+1}]} f(z)\, dz= \sum_{j=0}^{N-1} F_j(\gamma(t_{j+1})) - F_j(\gamma(t_{j})).\]

Der Ausdruck auf der rechten Seite ist allerdings auch definiert, falls \(\gamma\) nicht differenzierbar ist, was auf folgende Definition führt.

Definition 7.11

Es sei \(U\) offen und \(\gamma:[a,b]\to U\) ein Weg mit zulässiger Zerlegung \((t_0,\ldots,t_N)\) und offenen Kreisscheiben \(B_j,j=0,\ldots,N-1\). Für eine holomorphe Funktion \(f\) mit Stammfunktionen \(F_j\) auf \(B_j\) definieren wir

\[\int_\gamma f(z)\, dz = \sum_{j=1}^N F_j(\gamma(t_{j+1}))- F(\gamma(t_j)).\]

Remark 7.8

Für offenes \(U\subset\C\) und einen Weg \(\gamma:[a,b]\to U\) exsitiert stets eine zulässige Zerlegung und der Wert des Integrals ist unabhängig von der Wahl der Zerlegung, siehe [Nee17].

Mathematik für Physikstudierende C

Wegintegrale

Inhalt