Maß- und Integrationstheorie
5. Maß- und Integrationstheorie¶
Im ersten Semester haben wir bereits das Riemann Integral zur Berechnung des Flächeninhalts zwischen einer Funktion \(f \colon [a,b] \rightarrow \R\) und der x-Achse eingeführt (siehe Kapitel 7 in [Bur20]). Die grundlegende Idee hierbei war es die x-Achse in (unterschiedlich große) Intervalle zu unterteilen und mittels dieser Zerlegung Rechtecke zwischen dem Graphen der Funktion und der x-Achse zu konstruieren. Durch das Produkt der Seitenlängen dieser Rechtecke lässt sich nämlich deren Flächeninhalt leicht berechnen und die Summe all dieser Flächeninhalte approximiert den wahren Flächeninhalt zwischen dem Graphen und \(f\) und der x-Achse. Dieses Vorgehen ist zur Erinnerung nochmal in Abbildung Abb. 5.1 illustriert.
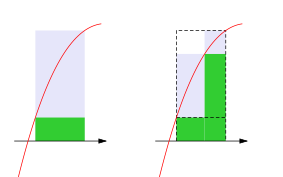
Abb. 5.1 Illustration zweier Approximationen des Riemann Integrals einer Funktion durch den Flächeninhalt von Rechtecken. Die grünen und lila Rechtecke visualisieren die Unter- bzw. Obersummen bezüglich des in rot dargestellten Graphen der Funktion. Quelle: Wikipedia; Riemannsches Integral.¶
Da wir bisher nur die Integration von eindimensionalen Funktionen auf kompakten Intervallen kennengelernt haben, wollen wir in diesem Kapitel den Begriff des Integals auf mehrdimensionale Funktionen \(f \colon \R^n \rightarrow \R\) erweitern. Das Riemann Integral lässt sich problemlos auf mehrdimensionalen Funktionen verallgemeinern, indem man das Integral nicht durch den Flächeninhalt von Rechtecken approximiert, sondern hierfür das Volumen von entsprechenden Quadern \(Q \subset \R^n\) berechnet. Es lässt sich insbesondere zeigen, dass jede stetige mehrdimensionale Funktion auf einem (nicht-ausgeartetem) Quader Riemann integrierbar ist.
Es hat sich jedoch in der Entwicklung der Mathematik herausgestellt, dass der Begriff des Riemann Integrals zu starke Forderungen an die zu Grunde liegenden Funktionen stellt und damit wichtige und interessante Funktionsklassen nicht integrierbar waren. Als Beispiel hierfür seien fraktale Mengen und Funktionen genannt, welche auch zur Modellierung von Prozessen in der Natur genutzt werden.
Aus diesem Grund hat sich ein eigenes Feld innerhalb der modernen Analysis gebildet - die sogenannte Maßtheorie. Es widmet sich hauptsächlich der Untersuchung von Maßen zur Berechnung von Längen, Flächen und Volumina in unterschiedlichen mathematischen Strukturen und Räumen. Es wird klar, dass Integration und die Berechnung von Volumina eng miteinander zusammen hängen, denn ist \(A\subset\R^n\) eine (messbare) Teilmenge, dann ist ihr Maß gleich dem Integral ihrer charakteristischen Funktion, d.h.,
In einem gewissen Sinn sind Maße ein fundamentaleres Konzept als das der Integration, da sich jede Integration auf die Berechnung von Maßen stützt.
Eins der berühmtesten Beispiele zur Motivation der Maßtheorie ist im Folgenden erklärt.
Example 5.1 (Dirichlet-Funktion)
Wir betrachten das kompakte Intervall \([0,1] \subset \R\) und definieren hierauf die sogenannte Dirichlet-Funktion \(\mathbb{1}_\Q \colon [0,1] \rightarrow \{0,1\}\) mit
Diese Abbildung kann als charakteristische Funktion der rationalen Zahlen \(\Q\) aufgefasst werden. Man sieht leicht ein, dass diese Funktion nicht Riemann-integrierbar ist, da alle Untersummen stets \(0\) und alle Obersummen stets \(1\) sind.
Um eine Funktion wie die Dirichlet-Funktion in Example 5.1 zu integrieren sieht man zunächst ein, dass die rationalen Zahlen \(\Q\) in den reellen Zahlen \(\R\) als abzählbare Menge eine sogenannte Nullmenge im Sinne der Maßtheorie repräsentieren. Wir werden im Laufe der Vorlesung die nötigen Werkzeuge der Maßtheorie einführen um diesen Umstand zu verstehen und einen verallgemeinerten Begriff des Integrals definieren, der diese Nullmenge berücksichtigt - das Lebesgue Integral. Dieses Integral ist eine echte Verallgemeinerung des Riemann Integrals und wir werden einsehen, dass die Menge der Lebesgue-integrierbaren Funktionen eine Obermenge der Menge der Riemann-integrierbaren Funktionen ist. Außerdem verhält sich das Lebesgue Integral bei Grenzwertbildungen einfacher als das Riemann Integral.
Als Referenz empfehlen wir hier wiederum das Skript von Prof.Dr.Hermann Schulz-Baldes (FAU) [SB18], aber besonders auch das Buch von Prof.Terence Tao zur Einführung in die Maßtheorie [Tao07] welches einen sehr intuitiven Einblick in die Materie gibt. Eine weitere sehr ausführliche Referenz, welche im Folgenden zitiert wird, ist das Buch von Prof.Vladimir I. Bogachev [Bog07].