1.3. Phasenflüsse und Phasenportraits¶

In diesem Abschnitt führen wir die grundlegende mathematischen Konzepte zur Analyse von kontinuierlichen dynamischen Systemen ein. Insbesondere diskutieren wir Flüsse als Lösungen von autonomen gewöhnlichen Differentialgleichungen und definieren sogenannte Phasenportraits, die es uns erlauben dynamische Systeme geometrisch zu interpretieren.

1.3.1. Phasenflüsse¶

Wir beginnen zunächst damit eine Klasse von Funktionen einzuführen, welche die Beschreibung zeitabhängiger Systeme vereinfacht. Die folgende Definition ist zunächst sehr allgemein für beliebige dynamische Systreme gehalten und wird später im Kontext von konkreten Anwendungsbeispielen spezieller diskutiert.

Definition 1.6 (Fluss und dynamisches System)

Sei \(U \subset \R^n\) eine offene Teilmenge und \(I=\R^+_0\), dann heißt eine Abbildung \(\Phi:I\times U\rightarrow U\) (Phasen-)Fluss, falls gilt,

\(\Phi(0, x) = x\) für alle \(x\in U\),
\(\Phi(t, \Phi(s,x)) = \Phi(s + t, \Phi(0, x)) = \Phi(s + t, x)\) für alle \(x\in U\) und alle \(s,t\in I\).

Das Tripel \((I, U, \Phi)\) heißt dynamisches System.

Zur Vereinfachung der Notation schreibt man häufig auch das erste Argument des Flusses als Index wie folgt

\[\Phi_t(x) \coloneqq \Phi(t, x).\]

Für die Analyse von dynamischen Systemen beschreibt der Fluss die Bewegung im Phasenraum in Abhängigkeit zur Zeit. Im Folgenden wollen wir speziell die Lösungen einer autonomen DGL

\[\dot{x} = F(x).\]

für \(F\in C^1(U;\R^n)\) als Fluss interpretieren. Hierbei soll das zweite Argument des Flusses jeweils den Anfangswert \(x_0\in U\) angeben und \(\Phi(x_0) = \Phi(\cdot, x_0)\) dann eine Lösung der DGL sein, d.h.,

\[\frac{\d}{\d t} \Phi(x_0) = F(\Phi(x_0))\]

So werden durch den Phasenfluss die Lösungen des dynamischen Systems in Abhängigkeit vom Anfangszustand angegeben. Im folgenden Beispiel betrachten wir den Fluss eines Vektorfeldes, das die rechte Seite eines gewöhnlichen Differentialgleichungssystems beschreibt.

Example 1.6

Sei \(I\subset \R_0^+\) ein offenes Zeitintervall. Wir interessieren uns für Lösungen des autonomen gewöhnlichen Differentialgleichungssystems

\[\dot{\vec{x}}(t) = F(\vec{x}) \quad \forall t\in I,\]

dessen rechte Seite durch das Vektorfeld \(F \colon \R^2 \rightarrow \R^2\) mit \(F(x,y) \, \coloneqq \, (y, -x)\) gegeben ist. Abbildung \xxx illustriert das Vektorfeld in \(\R^2\).

Wir wollen den Fluss des Vektorfeldes \(F\) angeben, der die Bewegung entlang der Lösungskurven der durch das Vektorfeld gegebenen gewöhnlichen Differentialgleichung beschreibt. Dieser ist gegeben durch

\[\Phi(t,(x,y)) = (\cos(t)x + \sin(t)y, -\sin(t)x + \cos(t)y).\]

Das die Funktion \(\Phi \colon I \times \R^2 \rightarrow \R^2\) ein Fluss ist, lässt sich leicht verifizieren durch Nachrechnen der beiden Eigenschaften eines Flusses aus Definition \ref.

1. Es gilt \(\Phi(0, (x,y)) = (x,y)\) für beliebige Paare \((x,y) \in \R^2\), da

\[\Phi(0, (x,y)) = (1\cdot x + 0\cdot y, - 0 \cdot x + 1 \cdot y) = (x,y).\]

2. Es gilt \(\Phi(t, \Phi(s,(x,y)) = \Phi(s + t, (x,y))\) für beliebige Paare \((x,y) \in \R^2\) und Zeitpunkte \(s,t \in I\), da wegen der Additionstheoreme von Sinus und Cosinus gilt

\[\begin{split}\Phi(t, \Phi(s,(x,y))) &= \Phi(t, (\cos(s)x + \sin(s)y, -\sin(s)x + \cos(s)y)) \\ &= [\cos(t)(\cos(s)x + \sin(s)y) + \sin(t)(-\sin(s)x + \cos(s)y), \\ & \ \ -\sin(t)(\cos(s)x + \sin(s)y) + \cos(t)(-\sin(s)x + \cos(s)y)]\\ &= \ [ (\cos(t)\cos(s) - \sin(t)\sin(s))x + (\cos(t)\sin(s) + \sin(t)\cos(s))y, \\ & \quad (-\sin(t)\cos(s) - \cos(t)\sin(s))x + (\cos(t)\cos(s) - \sin(t)\sin(s))y ] \\ &= (\cos(s+t)x + \sin(s+t)y, -\sin(s+t)x + \cos(s+t)y).\end{split}\]

Nun verfizieren wir noch, dass der Fluss tatsächlich Lösungen des gewöhnlichen Differentialgleichungssystems realisiert. Es gilt

\[\begin{split}\dot{\Phi}(t, (x,y)) &= \frac{d}{dt}(\cos(t)x + \sin(t)y, -\sin(t)x + \cos(t)y) \\&= (-\sin(t)x + \cos(t)y, -\cos(t)x - \sin(t)y) \\&= F(\Phi(t,(x,y)), \quad \forall t \in I, (x,y) \in U.\end{split}\]

Offensichtlich ist der Fluss \(\Phi \colon I \times \R^2 \rightarrow \R^2\) Lösung des gewöhnlichen Differentialgleichungssystems.

1.3.2. Lokale Flüsse¶

Nach dem Satz von Picard-Lindelöf Theorem 1.1 wissen wir, dass für jeden Anfangswert \(x_0\in U\) ein \(\epsilon(x_0)>0\) existiert, so dass es lokal eine eindeutige Lösung \(\phi: [-\epsilon(x_0), \epsilon(x_0)]\) gibt, falls die rechte Seite \(F\) lokal Lipschitzstetig bezüglich der \(y\)-Variablen ist. In diesem Fall müssen wir das Zeitintervall \(I(x_0)=[-\epsilon(x_0), \epsilon(x_0)]\) wählen und können also nicht wie in Definition 1.6 auf ganz \(I = \R^+_0\) als Zeitintervall arbeiten. Stattdessen können wir nur Tupel der Form \((t, x_0) \in I(x_0) \times \{x_0\}\) betrachten, wobei \(x_0\in U\) fixiert ist und \(t\) aus dem lokalen Existenzintervall \(I(x_0)\) gewählt werden kann.

Diese Einschränkung führt uns auf den Begriff des lokalen Phasenflusses.

Definition 1.7 (Lokaler Fluss)

Sei \(U \subset \R^n\) eine offene Teilmenge und der erweiterte Phasenraum \(G\subset \R^+_0\times U\) sei gegeben als

\[G = \bigcup_{x_0\in U} I(x_0) \times \{x_0\},\]

wobei \(0\in I(x_0)\) für jedes \(x_0\in U\) gelte.

Dann heißt eine Abbildung \(\Phi: G\rightarrow U\) lokaler (Phasen-)Fluss, falls

\(\Phi(0,x) = x\) für alle \(x\in U\),
\(\Phi(t, \Phi(s, x)) = \Phi(s+t, x)\) für alle \(x\in U\) und alle \(s,t\) mit \(s, s+t\in I(x)\) und \(t\in I(\Phi(s,x))\).

Im nächsten Lemma werden wir sehen, dass die Lösung eines autonomen gewöhnlichen Differentialgleichungssystems tatsächlich als solch ein lokaler Fluss interpretiert werden kann. In diesem Fall spircht man auch vom Fluss einer Differentialgleichung.

Lemma 1.3

Sei \(U\subset\R^n\) eine offene Teilmenge und es sei \(F \colon U \rightarrow \R^n\) eine lokal Lipschitzstetige Abbildung. Dann existieren Intervalle \(I(x_0)\), so dass es für den erweiterten Phasenraum

\[G = \bigcup_{x_0\in U} I(x_0)\times\{x_0\}\]

eine Funktion \(\Phi \colon G\rightarrow \R^n\) gibt, mit folgenden Eigenschaften

\(\frac{\d}{\d t} \Phi(t, x_0) = F(\Phi(t, x_0))\) für alle \((t,x_0)\in G\),
\(\Phi\) ist ein lokaler Fluss auf \(G\).

Proof. Da die rechte Seite \(F\) des autonomen gewöhnlichen Differentialgleichungssystems nach Voraussetzung lokal Lipschitzstetig ist, existiert nach dem Satz von Picard-Lindelöf Theorem 1.1 für jedes \(x_0\in U\) ein \(\epsilon(x_0)>0\), so dass eine Lösung des Differentialgleichungssystems \(\Phi_{x_0} \colon [-\epsilon(x_0),\epsilon(x_0)] \rightarrow U\) mit dem Anfangswert \(x_0\) existiert, d.h.,

\[\begin{split}\dot{\Phi}_{x_0}(t) &= F(\Phi_{x_0}(t)) \quad \forall t \in [-\epsilon(x_0),\epsilon(x_0)],\\ \Phi_{x_0}(0) &= x_0.\end{split}\]

Daher können wir den erweiterten Phasenraum als

\[G = \bigcup_{x_0\in U} [-\epsilon(x_0),\epsilon(x_0)] \times\{x_0\}\]

wählen und die Abbildung \(\Phi\) als Einschränkung auf die Funktionen \(\Phi_{x_0}\) so definieren, dass

\[\begin{split}\frac{\d}{\d t} \Phi(t, x_0) &= \dot{\Phi}_{x_0}(t) = F(\Phi_{x_0}(t)) = F(\Phi(t, x_0))\\ \Phi(0, x_0) &= \Phi_{x_0}(0) = x_0\end{split}\]

für alle \((t, x_0)\in G\). Damit haben wir sowohl die erste Aussage des Lemmas als auch die erste Flusseigenschaft aus Definition 1.6 gezeigt.

Die zweite Flusseigenschaft ist eine direkte Folgerung aus der Eindeutigkeit der Lösung des gewöhnlichen Differentialgleichungssystems. Wir führen den Beweis trotzdem im Folgenden explizit aus. Es sei \(x_0\in U, s\in [-\epsilon(x_0), \epsilon(x_0)]\) und zusätzlich \(t\) so gewählt, dass \(s+t \in [-\epsilon(x_0), \epsilon(x_0)]\) und \(t\in [-\epsilon(\Phi(s,x_0)), \epsilon(\Phi(s,x_0))]\). Per Definition löst die Funktion

\[\phi_1(\tau) \ \coloneqq \ \Phi(s + \tau, x_0)\]

sowie auch die Funktion

\[\phi_2(\tau) \ \coloneqq \ \Phi(\tau, \Phi(s,x_0))\]

das gewöhnliche Differentialgleichungssystem auf dem Intervall \([t, \epsilon(x_0)]\), da \(\Phi\) eine Lösung ist. Weiterhin wissen wir auf Grund der ersten Flusseigenschaft, dass

\[\phi_1(0) = \Phi(s, x_0) = \Phi(0, \Phi(s, x_0)) = \phi_2(0).\]

Somit stimmen also beide Funktionen an einem Punkt überein und sind somit schon auf dem gesamten Intervall \([t, \epsilon(x_0)]\) gleich, was eine direkte Folgerung aus dem Eindeutigkeitssatz 8.20 aus [Ten21] ist. Wir haben also insgesamt

\[\Phi(s + \tau, x_0) = \phi_1(\tau) = \phi_2(\tau) = \Phi(\tau, \Phi(s,x_0))\]

für jedes \(\tau\in [t, \epsilon(x_0)]\), was die zweite Flusseigenschaft aus Definition 1.6 zeigt.

1.3.3. Phasenporträts¶

Die teilweise abstrakten Konzepte und Eigenschaften von Phasenflüssen aus den vorangegangenen Abschnitten werden wir im Folgenden mit einfachen geometrischen Anschauungen illustrieren. Dafür benötigen wir zunächst die folgenden Definitionen.

Definition 1.8 (Phasenporträt)

Es sei \(\Phi:G\rightarrow U\) ein Phasenfluss eines gewöhnlichen Differentialgleichungssystems für den erweiterten Phasenraum \(G = I \times U\subset \R^+_0\times \R^n\). Dann können wir folgende Begriffe für den Fluss einführen:

Für jedes \(x_0\in U\) heißt die Funktion \(t\mapsto \Phi(t, x_0)\) Bahnkurve durch \(x_0\).
Die Menge \(\mathcal{O}(x_0) := \{\Phi(t, x_0): (t, x_0)\in G\}\) heißt Orbit oder Trajektorie durch \(x_0\).
Ein Punkt \(x_0 \in U\) heißt Ruhelage, falls \(\mathcal{O}(x_0) = \{x_0\}\).
Ein Anfangswert \(x_0\in U\) heißt periodisch mit Periode \(T>0\), falls \(\Phi(T, x_0) = x_0\).

Wir nennen die Zerlegung des erweiterten Phasenraums \(G\) in Orbits ein Phasenporträt des dynamischen Systems \((I,U, \Phi)\).

Phasenporträts erlauben es uns das charakteristische Verhalten kontinuierlicher dynamischer Systeme zu visualisieren und graphisch zu analysieren. An ihnen lassen sich beispielsweise die Existenz und Stabilität von Fixpunkten und periodischen Orbits direkt erkennen. Da ein Phasenporträt den gesamten Phasenraum zerlegt werden typischerweise nur einige charakteristische Orbits gezeichnet um die Übersichtlichkeit zu gewährleisten. Aus dem gleichen Grund beschränkt man sich in der Regel außerdem auf ein- und zweidimensionale Phasenräume.

Ein klassisches Beispiel aus der Mechanik ist besonders gut geeignet, um die eben eingeführten Konzepte näher zu diskutieren - die gedämpfte Schwingungsgleichung.

Example 1.7 (Gedämpfte Schwingungsgleichung)

Die gedämpfte Schwingungsgleichung ist gegeben durch

(1.7)¶\[m\ddot{x}(t) + r\dot{x}(t) + kx(t)=0\]

und beschreibt beispielsweise die horizontale (eindimensionale) Auslenkung eines Federpendels, das durch Reibungsverluste Schwingungsenergie über die Zeit verliert.

Hierbei bezeichnet

\(x(t)\) die horizontale Auslenkung des Federpendels zum Zeitpunkt \(t\),
\(m\) die Masse des Objekts,
\(r\) die Dämpfungskonstante,
\(k\) die Federkonstante.

Durch Einführung der Variablen \(p(t):= m\dot{x}(t)\) als Impuls erhalten wir das folgende gewöhnliche Differentialgleichungssystem

\[\begin{split}\dot{p}(t) &= - \frac{r}{m}p(t) -kx(t), \\ \dot{x}(t) &= \frac{1}{m}p(t).\end{split}\]

Dies lässt sich in kompakter Form schreiben als:

\[\begin{split}\begin{pmatrix} \dot{p} \\ \dot{x} \end{pmatrix}(t) = \begin{pmatrix} -\frac{r}{m} & -k \\ \frac{1}{m} & 0\end{pmatrix} \begin{pmatrix}p \\ x\end{pmatrix}(t)\end{split}\]

Betrachten wir speziell den ungedämpften Fall für \(r=0\), d.h. ohne Reibungsverluste, so geht die Gleichung in die Bewegungsgleichung für einen harmonischen Oszillator über. In diesem Fall erhalten wir zum Anfangswert \((p,x) \in U \subset \R^2 \) die Lösung

\[\begin{split}\Phi(t, (p,x)) = \begin{pmatrix} p \cos(\omega t) - m x \sin(\omega t) \\ \frac{p}{\omega m}\sin(\omega t) + x\cos(\omega t) \end{pmatrix},\end{split}\]

wobei \(\omega=\sqrt{\frac{k}{m}}\) die Eigenfrequenz des Systems ist.

Wir wollen im Folgenden die Phasenporträts der gedämpften Schwingungsgleichung und des harmonischen Oszillators illustrieren.

In beiden Abbildungen wird die horizontale Auslenkung \(x(t)\) des Federpendels auf der x-Achse und der Impuls \(p(t) = m\dot{x}(t)\) auf der y-Achse aufgetragen.

Das in Abb. 1.3 dargestellte Phasenportrait illustriert anschaulich, dass im Fall des harmonischen Oszillators ohne Dämpfung die Orbits elliptisch sind und somit jeder Startwert \(x_0 \in U\) periodisch ist.

# Dieser Code-Block definiert das Vektorfeld und den Fluss
import numpy as np

def F(x,p, m=1, r=0, k=1):
    return (1/m) * p, -k*x - (r/m) * p

def phi(x, p,  k=1, m=1, r=0, t_0=0, T=None, num_pts=40):
    omega = np.sqrt(k/m)
    delta = r/(2*m)
    
    if T is None:
        T = 2 * np.pi * 1/omega
    t = np.linspace(t_0, T, num_pts)
    
    sqrt = np.lib.scimath.sqrt
    
    lamda_1 = (-delta + sqrt(delta**2 - omega**2)) 
    lamda_2 = (-delta - sqrt(delta**2 - omega**2)) 
    
    c_2 = (p/m - lamda_1 * x)/(lamda_2 - lamda_1)
    c_1 = x - c_2
    
    phi_1 = np.real(c_1 * np.exp(lamda_1 * t) + c_2 * np.exp(lamda_2 * t))
    phi_2 = m*np.real(c_1 * lamda_1 * np.exp(lamda_1 * t) + c_2 * lamda_2 * np.exp(lamda_2 * t))
    
    #phi_1 = 1/(omega*m) * p * np.sin(omega * t) + x * np.cos(omega * t)
    #phi_2 = p * np.cos(omega * t) - m * x * np.sin(omega * t)
    
    return phi_1, phi_2

# Dieser Code Block produziert den Output und die Plots
import matplotlib.pyplot as plt
from matplotlib import cm
from myst_nb import glue

cmap = plt.get_cmap('viridis')
fig, ax = plt.subplots(1,2, figsize=(16,8))
num_pts = 20
size = 2
m = 0.5
k = 1
x = np.linspace(-size,size, num_pts)
p = np.linspace(-size,size, num_pts)
X, P = np.meshgrid(x, p)
X_Q, P_Q = F(X,P, m=m, k=k)
norms = np.sqrt(P_Q**2 + X_Q**2)
colors = cmap(norms/np.max(norms))
ax[0].quiver(X, P, X_Q, P_Q, color = np.reshape(colors, (num_pts**2, 4)))
ax[0].set_title('Vektorplot der Funktion F')
ax[0].set_aspect('equal')
ax[0].axis([-size,size,-size,size])
start_values = [(0.5,0), (1,0), (2,0), (3,0), (4,0)]
for (x,p) in start_values:
    phi_1, phi_2 = phi(x,p, m=m, k=k)
    color = cmap(np.sqrt(phi_1[0]**2 + phi_2[0]**2)/np.max(norms))
    ax[1].plot(phi_1, phi_2, color = color)
    for idx in np.linspace(0, len(phi_1)*3/4, 4):
        idx = int(idx)
        plt.arrow(phi_1[idx], phi_2[idx], phi_1[idx + 1] - phi_1[idx], phi_2[idx + 1] - phi_2[idx],
                  shape='full', lw=0, length_includes_head=True, head_width=.1, color = color)

ax[1].quiver(X, P, X_Q, P_Q, color = np.reshape(colors, (num_pts**2, 4)))
ax[1].set_aspect('equal')
ax[1].set_title('Phasenporträt')
ax[1].axis([-size,size,-size,size]);

glue("harmonic_oscillator", fig, display=False)

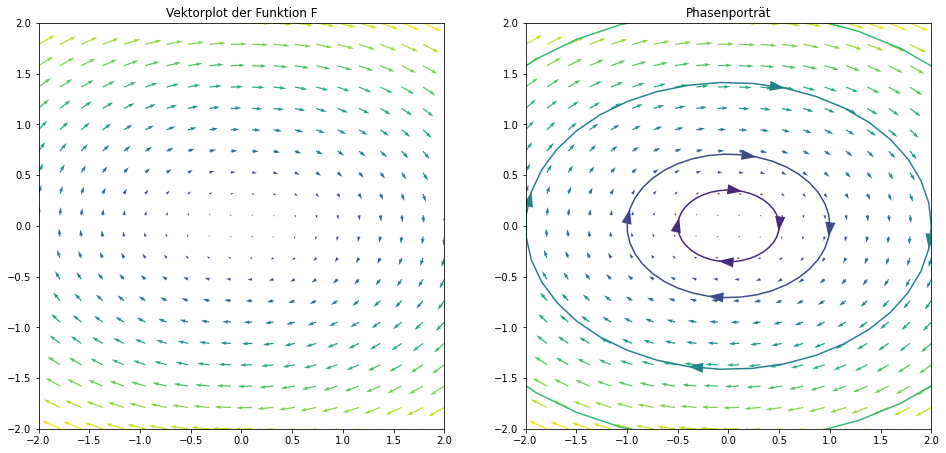
Abb. 1.3 Visualisierung des Phasenporträts und einiger Orbits für den Phasenfluss des harmonischen Oszillators aus Example 1.7. Das Phasenporträt zeigt das charakteristische Verhalten von Lösungen der gedämpften Schwingungsgleichung für reibungsfreie Prozesse, d.h., für eine Dämpfungskonstante \(r = 0\).¶

Betrachten wir nun für eine positive Dämpfungskonstante \(r > 0\) den Fall der allgemeinen gedämpften Schwingungsgleichung, so sieht man am dargestellen Phasenportrait in Abb. 1.4, dass die Trajektorien in den Ursprung konvergieren, der als Orbit in Ruhelage einen Fixpunkt des dynamischen Systems darstellt. Dies macht auch physikalisch Sinn, da jedes Federpendel auf Grund der Reibung nach endlicher Zeit zum Stillstand kommt.

# Dieser Code Block produziert den Output und die Plots
import matplotlib.pyplot as plt
from matplotlib import cm
from myst_nb import glue
import warnings
warnings.filterwarnings('ignore')
cmap = plt.get_cmap('viridis')
fig, ax = plt.subplots(1,2, figsize=(16,8))
num_pts = 20
size = 2
m = 0.5
k = 1
r = 0.3
x = np.linspace(-size,size, num_pts)
p = np.linspace(-size,size, num_pts)
X, P = np.meshgrid(x, p)
X_Q, P_Q = F(X,P, m=m, k=k, r=r)
norms = np.sqrt(P_Q**2 + X_Q**2)
colors = cmap(norms/np.max(norms))
ax[0].quiver(X, P, X_Q, P_Q, color = np.reshape(colors, (num_pts**2, 4)))
ax[0].set_title('Vektorplot der Funktion F')
ax[0].set_aspect('equal')
ax[0].axis([-size,size,-size,size])
start_values = [(0.0,0.5), (1,0), (0,-1.5), (-2,0), (0.0,2.5)]
for (x,p) in start_values:
    phi_1, phi_2 = phi(x,p, m=m, k=k,r=r, T=10, num_pts= 100)
    color = cmap(np.sqrt(phi_1[0]**2 + phi_2[0]**2)/np.max(norms))
    ax[1].plot(phi_1, phi_2, color = color)
    for idx in np.linspace(0, len(phi_1)*3/4, 4):
        idx = int(idx)
        plt.arrow(phi_1[idx], phi_2[idx], phi_1[idx + 1] - phi_1[idx], phi_2[idx + 1] - phi_2[idx],
                  shape='full', lw=0, length_includes_head=True, head_width=.1, color = color)

ax[1].quiver(X, P, X_Q, P_Q, color = np.reshape(colors, (num_pts**2, 4)))
ax[1].set_aspect('equal')
ax[1].set_title('Phasenporträt')
ax[1].axis([-size,size,-size,size]);

glue("damped_oscillator", fig, display=False)

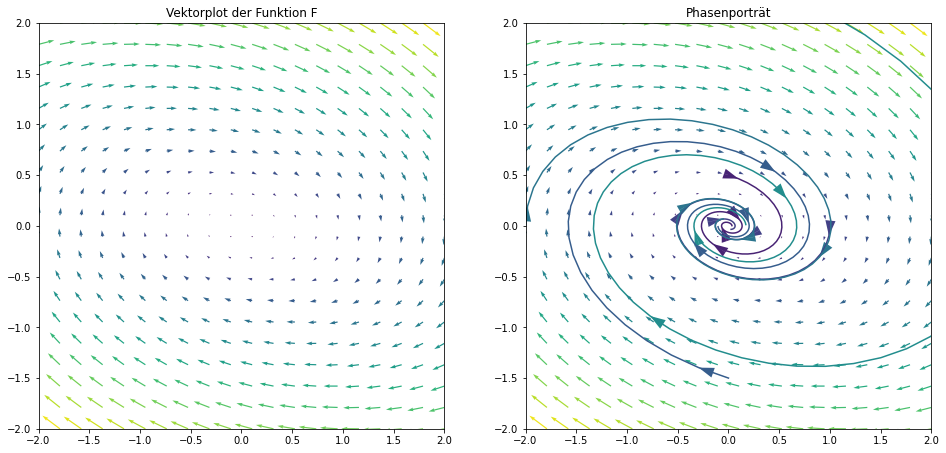
Abb. 1.4 Visualisierung des Phasenporträts und einiger Orbits für den Phasenfluss der gedämpften Schwingungsgleichung aus Example 1.7 für eine relativ groß gewählte Dämpfungskonstante \(r > 0\).¶

Mathematik für Physikstudierende C

Phasenflüsse und Phasenportraits

Inhalt

1.3. Phasenflüsse und Phasenportraits¶

1.3.1. Phasenflüsse¶

1.3.2. Lokale Flüsse¶

1.3.3. Phasenporträts¶