Navigation umschalten

.md .pdf

Repository

Inhalt

4.2. Tangentialräume und Tangentialbündel

4.2.1. Tangentialräume an Mannigfaltigkeiten

Aus dem Kapitel Linearisierung um Ruhelage ist bereits das Konzept der Linearisierung bekannt. Anschaulich gesprochen haben wir eine differenzierbare Funktion \(f\) durch ihre Linearisierung ersetzt um ein einfacheres Problem zu erhalten. Dieses Konzept soll nun auf glatte Mannigfaltigkeiten übertragen werden.

Wir haben bereits erkannt, wie wir den Begriff der Differenzierbarkeit einer Funktion auf einer Mannigfaltigkeit definieren. Und obwohl die Frage nach der Differenzierbarkeit einer Funktion nach Lemma 4.2 kartenunabhängig ist, so stellt sich heraus, dass der tatsächliche Wert der Ableitung einer Verknüpfung \(f \circ\phi^{-1}\) noch immer von der konkreten Wahl des Homöomorphismus \(\phi\) abhängt. Um auch hier die gewünschte Kartenunabhängigkeit zu erreichen, brauchen wir einen anderen Begriff der Differenzierbarkeit. Hierbei wird uns der sogenannte Tangentialraum helfen. Man kann ihn als eine Linearisierung der Mannigfaltigkeit \(\M\) an einem Punkt \(p\in\M\) interpretieren.

Das folgende Beispiel erklärt anschaulich den Tangentialraum an eine Mannigfaltigkeit.

Example 4.3

Wir betrachten zunächst den Einheitskreis \(\M = \mathbb{S}^1\) und den Punkt \(p = (1, 0)^T \in \mathbb{S}^1\). Der Tangentialraum \(T_p\M\) an \(\M\) im Punkt \(p\) ist der eindimensionale Unterraum

\[T_p\M = \lbrace \lambda \cdot (0, 1)^T : \lambda \in \R \rbrace \subset \R^2.\]

Es gibt in der Literatur zwei verschiedene, jedoch äquivalente Arten den Tangentialraum zu definieren.

• Geometrischer Tangentialraum: Bei diesem Ansatz wählt man eine geometrisch Anschauung und definiert den Tangentialraum durch Richtungsvektoren, die am Punkt \(p\in\M\) anliegen. Der Vorteil dieser Definition ist es, dass sie intuitiv und geometrisch anschaulich ist.

• Algebraische Defnition: Bei diesem Ansatz führt man den Tangentialraum mittels spezieller linearer Abbildungen, genannt Derivationen, zurück. Man verliert hierbei zwar die geometrische Anschauung, allerdings ist das Konzept relativ einfach zu formulieren und hilft die Sachverhalte auf algebraische Zusammenhänge zurückzuführen.

In der Praxis (und in vielen Mathematikbüchern) werden beide Definitionen nebeneinander verwendet und die jeweilige Interpretation geht dann aus dem Kontext hervor. Da sich die beiden Konzepte somit schlecht voneinander trennen lassen werden wir im Folgenden den geometrischen Tangentialraum \(T^{\text{geo}}_p\M\) und den algebraischen Tangentialraum \(T^{\text{alg}}_p\M\) explizit einführen und anschließend eine Isomorphie

\[T^{\text{geo}}_p\M\cong T^{\text{alg}}_p\M\]

zwischen den beiden Tangentialräumen zeigen.

Gefahr

In der Literatur wird diese explizite Unterscheidung oft nicht vorgenommen. Stattdessen wird der Tangentialraum einfach nur \(T_p\M\) genannt. Elemente dieses Raums sind dann je nach Kontext geometrisch oder algebraisch zu interpretieren.

4.2.1.1. Geometrische Definition

Von der Differentiation im Mehrdimensionalen ist bereits das Konzept der Richtungsableitung bekannt (siehe Kapitel 6.2.2 in [Ten21]). Hierbei betrachtet man für eine Funktion \(F:\R^n\to\R\) den Strahl \(\gamma(t):= x + t\cdot v\), wobei \(x,v\in\R^n\) und den Grenzwert

\[\lim_{t\to 0} \frac{F(\gamma(t)) - F(\gamma(0))}{t} = \frac{F(x + t\cdot v) - F(x))}{t}.\]

Wir werden dieses Konzept nun auf glatte \(n\)-dimensionale Mannigfaltigkeiten \(\M\) verallgemeinern, indem wir anstatt von Strahlen differenzierbare Kurven auf der Mannigfaltigkeit betrachten.

Definition 4.12 (Differenzierbare Kurve)

Sei \(\M\) eine glatte Mannigfaltigkeit und sei

\[\gamma \colon (-1,1) \rightarrow \M\]

eine Kurve auf der Mannigfaltigkeit \(\M\). Wir nennen \(\gamma\) differenzierbar im Punkt \(0\in(-1,1)\), falls die Kurve stetig ist und falls eine Karte \((U,\phi)\) von \(\M\) existiert, so dass für genügend kleines \(\varepsilon\) auch \(\gamma((-\varepsilon,\varepsilon))\subset U\) gilt und die Verknüpfung

\[\phi \circ \gamma:(-\varepsilon,\varepsilon)\to\R^n\]

differenzierbar in \(0\) ist .

Wir werden im Folgenden ausschließlich die Ableitung der Kurve im Punkt \(t=0\) betrachten und sprechen deshalb verkürzt einfach nur von differenzierbaren Kurven. Zusätzlich sei zu bemerken, dass die obige Definition nicht von der Wahl der Karte abhängt.

Example 4.4

Es sei \(\M=\S^2\) die Einheitssphäre und \(f:\M\to\R\) beschreibe eine Wärmeverteilung auf deren Oberfläche. Betrachtet man nun die Bahn eines Partikels auf der Oberfläche beschrieben durch die Kurve \(\gamma:(-t, t)\to \M\) so erhalten wir eine eindimensionale Abbildung

\[f\circ\gamma:(-t,t)\to \R,\]

die zu jedem Zeitpunkt die Temperatur des Ortes, an dem sich der Partikel befindet, beschreibt.

Abb. 4.4 Visualisierung einer Kurve auf der oberen Hälfte der Einheitssphäre im \(\R^3\).

Mit Hilfe von differenzierbaren Kurven auf Mannigfaltigkeiten können wir im Folgenden die Richtungsableitung an einer Mannigfaltigkeit definieren.

Definition 4.13 (Richtungsableitung an Mannigfaltigkeit)

Es sei \(\M\) eine glatte Mannigfaltigkeit, \(\gamma:(-1,1)\to\M\) eine differenzierbare Kurve mit \(\gamma(0)=p\in\M\) und \(f \in C^\infty(\M)\) eine glatte Funktion. Dann nennen wir die Abbildung

\[\begin{split}D_\gamma : C^\infty(\M) &\to \R\\ f &\mapsto D_\gamma(f):=\frac{d}{dt}(f\circ \gamma)\big\rvert_{t=0}\end{split}\]

Richtungsableitung von \(f\) durch \(\gamma\) im Punkt \(p\).

Betrachten wir nun eine differenzierbare Kurve \(\gamma \colon (-1, 1) \rightarrow \M\) mit \(\gamma(0)=p \in \M\) und eine glatte Funktion \(f \in \C^\infty(\M)\) definiert auf einer glatten Mannigfaltigkeit \(\M\). Dann können wir die Richtungsableitung \(D_\gamma(f)\) mit Hilfe der Kettenregel für die Differentiation darstellen als

\[D_\gamma(f) = \frac{d}{dt}(f\circ \gamma)\big\rvert_{t=0} = \frac{d}{dt}\big( (f\circ \phi^{-1}) (\phi \circ \gamma) \big)\rvert_{t=0} = \big(D(f\circ \phi^{-1})\big)(\phi(p))\cdot \frac{d}{dt}(\phi \circ \gamma)\rvert_{t=0}\]

und für eine weitere differenzierbare Kurve \(\eta \colon (-1, 1) \rightarrow \M\) mit \(\eta(0)=p\) erhalten wir analog

\[D_\eta(f) = \frac{d}{dt}(f\circ \eta)\big\rvert_{t=0} = \big(D(f\circ \phi^{-1})\big)(\phi(p))\cdot \frac{d}{dt}(\phi \circ \eta)\rvert_{t=0}.\]

Wir erkennen also, dass der Wert der Richtungsableitung in der Tat von der Kurve \(\gamma\) abhängt. Dies führt auf einen natürlichen Äquivalenzbegriff von Kurven, wie die folgende Bemerkung beschreibt.

Remark 4.3 (Tangentialvektoren)

Es sei \(\M\) eine glatte \(n\)-dimensionale Mannigfaltigkeit, \(p\in\M\) ein Punkt auf der Mannigfaltigkeit und \((U,\phi)\) eine Karte von \(\M\), für die gilt, dass \(p\in U\) ist. Für zwei differenzierbare Kurven \(\gamma, \eta:(-1,1) \to U\) mit \(\gamma(0) = \eta(0) = p\) ist die Relation

\[\gamma \sim_p \eta \qquad \Leftrightarrow \qquad \frac{d}{dt}(\phi \circ \gamma)\rvert_{t=0} = \frac{d}{dt}(\phi \circ \eta)\rvert_{t=0}\in \R^n\]

eine Äquivalenzrelation (siehe Kapitel 2.1.1 in [Bur20]). Insbesondere ist die Äquivalenzklasse unabhängig von der Wahl des Homöomorphismus \(\phi\).

Mittels der oben beschriebenen Äquivalenzrelation sind wir in der Lage den Begriff der Tangentialvektoren und des Tangentialraums zu definieren.

Definition 4.14 (Geometrische Tangentialvektoren und Tangentialraum)

Es sei \(\M\) eine glatte \(n\)-dimensionale Mannigfaltigkeit, \(p\in\M\) ein Punkt auf der Mannigfaltigkeit und \((U,\phi)\) eine Karte von \(\M\), für die gilt, dass \(p\in U\) ist.

Die Äquivalenzklasse \(\gamma^\prime(0):=[\gamma]_{\sim_p}\) wird als geometrischer Tangentialvektor an \(\M\) im Punkt \(p\) bezeichnet. Der Raum der (geometrischen) Tangentialvektoren

\[T_p^{\text{geo}}\M := \{\gamma^\prime(0): \gamma\text{ ist differenzierbare Kurve mit }\gamma(0)=p\}\]

heißt geometrischer Tangentialraum der Mannigfaltigkeit \(\M\) am Punkt \(p \in \M\).

Der Tangentialraum induziert sogar eine Vektorraumstruktur wie folgende Bemerkung festhält.

Remark 4.4

Es sei \(\M\) eine glatte \(n\)-dimensionale Mannigfaltigkeit, \(p\in\M\) ein Punkt auf der Mannigfaltigkeit und \((U,\phi)\) eine Karte von \(\M\), für die gilt, dass \(p\in U\) ist. Sei außerdem \(\gamma \colon (-1,1) \rightarrow \M\) eine differenzierbare Kurve auf \(\M\) mit \(\gamma(0) = p\). Wir definieren nun die folgende Bijektion auf dem Tangentialraum

\[\begin{split}d\phi\rvert_p \colon T^{\text{geo}}_p\M &\rightarrow \R^n,\\ [\gamma]_{\sim_p} &\mapsto d\phi\rvert_p (\gamma^\prime(0)) := (\phi \circ \gamma)^\prime (0).\end{split}\]

Basierend auf dieser Abbildung lassen sich die folgenden Operationen für den Punkt \(p \in \M\) definieren

\[\begin{split}\gamma^\prime(0) +_{p} \eta^\prime(0) \ &:= \ (d\phi\rvert_p)^{-1}\big[d\phi\rvert_p(\gamma^\prime(0)) + d\phi\rvert_p(\eta^\prime(0))\big]\\ \lambda \cdot_p \gamma^\prime(0) \ &:= \ (d\phi\rvert_p)^{-1} (\lambda \cdot d\phi\rvert_p(\gamma^\prime(0))\end{split}\]

Insgesamt ergibt somit das Tripel \((T_p^{\text{geo}}\M, +_p, \cdot_p)\) einen reellen Vektorraum. Man bemerke, dass die oben definierten Abbildungen erneut unabhängig von der Wahl des Homöomorphismus \(\phi\) sind.

4.2.1.2. Algebraische Definition

Alternativ zur geometrischen Herleitung lässt sich der Tangentialraum auch algebraisch definieren über sogenannte Derivationen. Hierbei beschreiben wir Tangentialvektoren nun nicht mehr als Kurven, sondern als spezielle Funktionale, welche durch ihre Wirkung auf \(C^\infty(\M)\) charakterisiert sind. Die Motivation hierbei soll die Richtungsableitung aus Definition 4.13 sein und speziell die im folgenden Lemma beschriebenen Eigenschaften.

Lemma 4.3

Es sei \(\M\) eine glatte Mannigfaltigkeit und \(p\in\M\) und \(\gamma:[-1,1]\to\M\) eine glatte Kurve durch \(p\). Dann gilt für die Richtungsableitung \(D_\gamma:C^\infty(\M)\to\R\),

• \(D_\gamma\in (C^\infty(\M))^\ast\),

• Für \(f,g\in C^\infty(\M)\) gilt: \(\ D_\gamma(fg) = D_\gamma(f) g(p) + f(p) D_\gamma(g)\).

Proof. Siehe Übung.

Die zweite Eigenschaft wird auch Produktregel oder Leibnizregel genannt. Wir wollen nun im Folgenden nicht nur Richtungsableitungen betrachten, sondern allgemeine Funktionale, die diese Eigenschaft erfüllen.

Definition 4.15 (Derivation und algebraischer Tangentialraum)

Es sei \(\M\) eine glatte Mannigfaltigkeit und \(p\in\M\) ein Punkt der Mannigfaltigkeit. Wir nennen eine lineare Abbildung \(D: C^\infty(\M) \to \R\) eine Derivation an \(p\), falls sie die folgende Produktregel erfüllt,

\[D(fg) = D(f) g(p) + f(p) D(g).\]

Der Raum der Derivationen an \(p\)

\[T^{\text{alg}}_p\M := \{D\in C^\infty(\M)^\ast: D\text{ ist Derivation an }p\}\]

wird als algebraischer Tangentialraum bezeichnet.

Über die Menge der Derivation erhalten wir auf natürliche Art einen Vektorraum da per Definition

\[T^{\text{alg}}_p\M \subset (C^\infty(\M))^\ast\]

gilt. Somit erbt der algebraischer Tangentialraum die Vektorraumoperationen von \(C^\infty(\M)^\ast\) und es muss lediglich nachgeprüft werden, dass diese Teilmenge noch immer ein Vektorraum, also inbesondere abgeschlossen ist.

Lemma 4.4

Es sei \(\M\) eine glatte Mannigfaltigkeit und \(p\in\M\) ein Punkt der Mannigfaltigkeit. Dann ist \(T^{\text{alg}}_p\M\) ein reeller Vektorraum.

Proof. Siehe Übung.

Wie der Name schon erkennen lässt haben Derivationen gewisse Eigenschaften, die von der Ableitungsoperation bekannt sind. So bildet zum Beispiel jede Derivation konstante Funktionen auf \(0\) ab, wie das folgende Lemma zeigt.

Lemma 4.5 (Derivation konstanter Funktionen)

Es sei \(\M\) eine glatte Mannigfaltigkeit und \(p\in\M\) ein Punkt der Mannigfaltigkeit. Außerdem sei \(f\in C^\infty(\M)\) eine konstante Funktion, d.h., es existiert eine Konstante \(c\in\R\), so dass

\[f(q) = c\quad\forall q\in\M.\]

Dann gilt schon \(D(f)=0\) für alle Derivationen \(D\in T^{\text{alg}}_p\M\).

Proof. Es sei \(D\in T^{\text{alg}}_p\M\) eine beliebige Derivation an den Punkt \(p \in \M\). Wir betrachten zunächst die konstante Einsfunktion

\[\begin{split}g:\M &\to \R\\ q &\mapsto g(x) := 1.\end{split}\]

Dann gilt mit der Produktregel für Derivationen

\[D(g) = D(g\cdot g) = D(g)\,g(p) + g(p)\, D(g) = 2\,D(g)\]

und somit muss schon \(D(g) = 0\) gelten. Wir können die konstante Funktion \(f\) nun darstellen als \(f= c\,g\) und unter Ausnutzung der Linearität von \(D\) erhalten wir schon

\[D(f) = D(c\,g) = c\,D(g) = 0.\]

Wir haben nun zwei verschiedene Arten gesehen den Tangentialraum einzuführen. Tatsächlich sind diese Definitionen äquivalent in dem Sinn, dass ein Isomorphismus zwischen dem geometrischen und algebraischen Tangentialraum existiert.

Theorem 4.1 (Isomorphie zwischen alg. und geom. Tangentialraum)

Es sei \(\M\) eine glatte Mannigfaltigkeit und \(p\in\M\) ein Punkt der Mannigfaltigkeit. Dann gilt die folgende Isomorphie

\[T^{\text{geom}}_p\M \ \cong \ T^{\text{alg}}_p\M.\]

Proof. Siehe z.B. Kapitel 2.3 in [Janich03].

4.2.1.3. Basis des algebraische Tangentialraums

Wir wollen in diesem Abschnitt eine Basis des algebraischen Tangentialraums konstruieren. Im Euklidischen Raum können wir auf natürliche Art die Koordinatenrichtungen als Kurven wählen, also Funktionen der Form

\[t \mapsto t e_i\]

für \(i=1,\ldots,n\), wobei \(e_i\) den \(i\)-ten Einheitsvektor in \(\R^n\) bezeichnet. Um diese Idee auf Mannigfaltigkeiten zu übertragen wählen wir eine Karte \(\varphi:\M\to\R^n\), wobei man hier auch von

\[\varphi = (\varphi_1,\ldots,\varphi_n) =: (x^1,\ldots,x^n)\]

als einem lokalen Koordinatensystem spricht. Wir erhalten somit Kurven

\[\gamma_{x^i}(t):= \varphi^{-1}(\varphi(p) + t e_i)\]

und mithilfe der Richtungsableitung aus Definition 4.13 die Derivationen

\[\begin{split}\partial_{x^i}^p: C^\infty(\M) &\to \R\\ f &\mapsto \partial_{x^i}^p(f) := \frac{d}{dt} (f\circ \gamma_{x^i}(t))\big\rvert_{t=0}.\end{split}\]

Definition 4.16 (Partielle Derivation)

Sei \(\M\) eine glatte \(n\)-dimensionale Mannigfaltigkeit für \(n\in\N\) und sei \(f \in C^\infty(\M)\) eine glatte Funktion. Dann bezeichnen wir die Derivationen

\[\partial_{x^i}^p (f) := \frac{d}{dt} (f\circ \gamma_{x^i}(t))\big\rvert_{t=0}, \quad i=1,\ldots,n\]

als partielle Derivationen von \(f\) im Punkt \(p \in \M\).

Wir interpretieren also im Folgenden das Symbol \(\partial_{x^{i}}^p\) als Derivation an \(p\in\M\), d.h., insbesondere als lineare Abbildung von \(C^\infty(\M)\) nach \(\R\). Diese partiellen Derivationen folgen der Intuition, dass die partielle Ableitung in eine Richtung auch nur Änderungen in diese Richtung respektiert. Wir formalisieren diese Anschauung in folgendem Lemma.

Lemma 4.6

Es sei \(\M\) eine glatte Mannigfaltigkeit, \(p\in\M\) ein Punkt der Mannigfaltigkeit und \((U,\varphi)\) sei eine Karte mit \(p\in U\). Dann gilt für die partielle Derivation

\[\partial_{x^i}^p(\varphi_j) = \delta_{ij},\]

wobei \(\delta_{ij}\) das Kronecker-Delta bezeichnet.

Proof. Wir betrachten zunächst die Funktion \(\varphi_j \circ \gamma_{x^i}\) und erhalten für \(t\in [-1,1]\)

\[\begin{split}\varphi_j \circ \gamma_{x^i}(t) &= \varphi_j \circ \varphi^{-1}(\varphi(p) + t e_i)\\ &= (\varphi(p) + t e_i)_j\\ &= \begin{cases} \varphi_i(p) + t e_i &\text{ für } i=j,\\ \varphi_j(p)&\text{ sonst}. \end{cases}\end{split}\]

Somit gilt schon für die partielle Derivation

\[\begin{split}\partial_{x^i}^p(\varphi_j)= \frac{d}{dt} (\varphi_j \circ \gamma_{x^i}(t))\big\rvert_{t=0} = \begin{cases} 1&\text{ für } i=j,\\ 0&\text{ sonst}. \end{cases}\end{split}\]

Das folgende Hauptresultat dieses Abschnitts erlaubt es uns beliebige Derivationen mithilfe der partiellen Derivationen darzustellen, da diese eine Basis des algebraischen Tangentialraums bilden.

Theorem 4.2

Es sei \(\M\) eine \(n\)-dimensionale glatte Mannigfaltigkeit. Dann bildet die Menge

\[\{\partial_{x^1}^p,\ldots,\partial_{x^n}^p\}\]

eine Basis des algebraischen Vektorraums \(T^{\text{alg}}_p\). Insbesondere gilt

\[\dim(T^{\text{alg}}_p)=\dim(T^{\text{geom}}_p)=n\]

Proof. Es sei \((U,\varphi)\) eine Karte der Mannigfaltigkeit \(\M\) und wir nehmen ohne Beschränkung der Allgemeinheit an, dass \(\varphi(p)=0 \in \R^n\) gilt, was stets durch eine entsprechende Translation des Koordinatensystems erreicht werden kann. Zusätzlich wählen wir einen Radius \(r>0\) klein genug, so dass \(B_r(0) \subset \varphi(U)\) gilt und betrachten als Karte \(\tilde{\varphi} := \varphi\rvert_{\tilde{U}}\), d.h., die Einschränkung von \(\varphi\) auf \(\tilde{U}:= \varphi^{-1}(B_r(0))\). Wir können die Karte \(\tilde{\varphi}\) wegen der Kartenunabhängigkeit des Tangentialraums und der Tatsache, dass \((\tilde{U},\tilde{\varphi})\) auch eine Karte der Mannigfaltigkeit \(\M\) mit \(p\in \tilde{U}\) ist, betrachten. Da das Bild von \(\tilde{\varphi}\) nun der gesamte Ball \(B_r(0) \subset \R^n\) ist, können wir nun Strecken von \(0\) zu einem beliebigen Punkt in \(B_r(0)\) betrachten, welche selbst ganz im Bild von \(\tilde{\varphi}\) enthalten sind.

Sei nun \(f\in C^\infty(\M)\) eine beliebige glatte Funktion. Dann definieren wir die Funktion \(g:= f\circ \tilde{\varphi}^{-1}\) für die insbesondere \(g\in C^\infty(\R^n)\) gilt. Für einen beliebigen Punkt \(q\in\tilde{U}\) erhalten wir einen Richtungsvektor \(z:=\tilde{\varphi}(q)\in B_r(0)\) und können somit die Einschränkung von \(g\) auf die eindimensionale Strecke zwischen \(0\) und \(z\) in \(\R^n\) betrachten, d.h.,

\[\begin{split}\tilde{g}:[0,1] &\to\R\\ t&\mapsto g(t\cdot z).\end{split}\]

Hierbei sieht man erneut ein, dass \(\tilde{g}\in C^\infty([0,1])\) gilt. Dies bedeutet insbesondere, dass wir den Hauptsatz der Differential- und Integralrechnung (vgl. Theorem 5.3 in [Ten21]) anwenden können und somit erhalten wir

\[\tilde{g}(1) = \tilde{g}(0) + \int_{0}^1 \tilde{g}^\prime(t)\,\mathrm{d}t.\]

Wir berechnen die Ableitung im Integral als Richtungsableitung und erhalten,

\[\int_{0}^1 \tilde{g}^\prime(t) \,\mathrm{d}t =\int_{0}^1 \langle \nabla g (t\cdot z), z \rangle \,\mathrm{d}t =\sum_{i=1}^{n} \int_{0}^1 \partial_i g (t\cdot z) \cdot z_i \,\mathrm{d}t.\]

Da per Definition

\[\tilde{g}(1) = g(z)=f(q)\]

und

\[\tilde{g}(0) = g(0) = g(\varphi(p))=f(p)\]

gilt, folgt daraus

\[f(q) = f(p) + \sum_{i=1}^{n} \varphi_i(q)\ \cdot \underbrace{\int_{0}^1 \partial_i (f\circ \varphi^{-1})(t\cdot \varphi(q)) \, \mathrm{d}t}_{:=F_i(q)}.\]

An diesem Punkt bemerken wir, dass \(f\circ \varphi^{-1} \in C^\infty(\R^n)\) eine klassisch differenzierbare Funktion ist, wobei \(f\) eine glatte Funktion auf der Mannigfaltigkeit \(\M\) darstellt. Wenden wir nun die \(j\)-te partielle Derivation auf \(f\) an, erhalten wir unter Ausnutzung der Linearität der Abbildung \(\partial_{x^j}^p\)

\[\partial_{x^j}^p (f) = \underbrace{\partial_{x^j}^p (f(p))}_{=0} + \sum_{i=1}^{n} \partial_{x^j}^p(\varphi_i \cdot F_i) = \sum_{i=1}^{n} \partial_{x^j}^p(\varphi_i \cdot F_i)\]

wobei wir Lemma 4.5 und die Tatsache, dass \(\varphi_i, F_i\in C^\infty(\M)\) gilt, benutzt haben. Weiterhin gilt wegen der Leibnizregel

\[\partial_{x^j}^p(\varphi_i \cdot F_i(q)) = \underbrace{\partial_{x^j}^p(\varphi)}_{=\delta_{ij}} F_i(p)+ \underbrace{\varphi_i(p)}_{=0} \partial_{x^j}^p(F_i),\]

wobei wir Lemma 4.6 und \(\varphi(p)=0\) verwendet haben. Somit folgt schon

\[\partial_{x^j}^p (f) = F_j(p)\]

und damit insbesondere

\[f = f(p) + \sum_{i=1}^{n} \varphi_i \partial_{x^i}^p(f).\]

Dies bedeutet aber schon, dass die partiellen Derivationen ein Erzeugendensystem des algebraischen Tangentialraums bilden, denn sei \(D\in T^{\text{alg}}_p\) eine beliebige Derivation, dann gilt

\[D(f) = \underbrace{D(f(p))}_{=0} + \sum_{i=1}^n D(\varphi_i) \partial_{x^i}^p(f).\]

Dies bedeutet, dass jede Derivation \(D\) über eine Linearkombination aus partiellen Derivationen dargestellt werden kann, wobei die Koeffizienten durch \(D(\varphi_i)\) gegeben sind.

Es bleibt die Eindeutigkeit der Darstellung zu zeigen. Seien dazu Koeffizienten \(\alpha_i \in \R, i=1,\ldots,n\) gegeben, so dass für jede Funktion \(f\in C^\infty(\M)\) gilt

\[D:= \sum_{i=1}^n \alpha_i \partial_{x^i}^p(f) = 0.\]

Durch erneute Anwendung von Lemma 4.6 erhalten wir aber, dass

\[0 = D(\varphi_j) = \alpha_j \]

für alle \(j=1,\ldots,n\) und somit haben wir die lineare Unabhängigkeit bewiesen.

Insgesamt bilden also die partiellen Deriviationen eine Basis des algebraischen Tangentialraums und es gilt

\[\dim(T^{\text{alg}}_p)=\dim(T^{\text{geom}}_p)=n.\]

4.2.1.4. Kotangentialraum

Da wir den Tangentialraum \(T^{\text{alg}}_p\) als Vektorraum identifiziert haben, können wir auch dessen algebraischen Dualraum in der folgenden Definition betrachten.

Definition 4.17 (Kotangentialraum)

Es sei \(\M\) eine glatte Mannigfaltigkeit. Dann bezeichnen wir mit

\[T_p^\ast\M:= (T_p^{\text{alg}}\M)^\ast\]

den algebraischen Dualraum des Tangentialraums, welcher häufig Kotangentialraum genannt wird.

Remark 4.5

Ein Element \(\delta\in T_p^\ast\M\) ist also eine lineare Abbildung

\[\delta: T_p^{\text{alg}}\M \to \R,\]

die eine Derivation \(D\in C^\infty(\M)^\ast\) auf eine reelle Zahl \(\delta(D)\in\R\) abbildet.

Die folgende Definition beschreibt ein wichtiges Element des Kotangentialraums.

Definition 4.18 (Totales Differential)

Sei \(f\in\C^\infty(\M)\) eine beliebige glatte Funktion auf einer Mannigfaltigkeit \(\M\). Dann bezeichnen wir das Element \(\mathrm{d}f_p \in T_p^\ast\M\) mit

\[\begin{split}\mathrm{d}f_p: T_p^{\text{alg}}\M &\to\R\\ D_p &\mapsto \mathrm{d}f_p(D):= D_p(f).\end{split}\]

als totales Differential der Funktion \(f\) im Punkt \(p \in \M\).

Insbesondere können wir das totale Differential \(df\) mit einer glatten Funktion aus \(C^\infty(M)\) identifizieren, was den Zusammenhang von \(T^\ast_p \M\) als Bidualraum von \(C^\infty(\M)\) unterstreicht.

Die Basis von \(T^\ast_p\) wird kanonisch als duale Basis (siehe Lemma 3.3) gewählt. Jeder Vektor \(v\in T_p^{\text{alg}}\M\) hat somit eine eindeutige Darstellung

\[v = \sum_{i=1}^n \alpha_i \partial_{x^i}.\]

Wir wählen nun Abbildungen \(\mathrm{d}x^i\in T^\ast_p\M, i=1,\ldots,n\) gerade so, dass

\[\mathrm{d}x^i(v) = \alpha_i\]

gilt. Das folgende Lemma zeigt, dass es sich hierbei um eine Basis von \(T^\ast_p\M\) handelt.

Lemma 4.7

Es sei \(\M\) eine glatte Mannigfaltigkeit und \(p\in\M\). Dann ist die Menge

\[\{\mathrm{d}x^1,\ldots, \mathrm{d}x^n\}\]

eine Basis von \(T_p^\ast\M\).

Proof. Die Aussage folgt direkt aus Lemma 3.3.

4.2.2. Tangentialbündel

Bemerkung

Im Folgenden bezeichne \(T_p\M\in\{T^{\text{alg}}_p\M, T^{\text{geom}}_p\M \}\) entweder den algebraischen oder den geometrischen Tangentialraum. Die konkrete Wahl wird an den entsprechenden Stellen (wenn nötig) spezifiziert.

Bisher haben wir für eine \(n\)-dimensionale glatte Mannigfaltigkeit \(\M\) für jeden einzelnen Punkt \(p\in\M\) den zugehörigen Tangentialraum \(T_p\M\) betrachtet, welcher wiederum wegen Theorem 4.2 isomorph zum \(\R^n\) ist. Wir interessieren uns jetzt dafür, wie sich Tangentialräume für verschiedene Punkte \(p,q\in \M\) in Beziehung setzen lassen. Darüber hinaus wollen wir eine globale Struktur definieren welche alle Tangentialräume (d.h. für jedes \(p\in\M\)) zusammenfasst.

In diesem Kontext spricht man von der Mannigfaltigkeit häufig als dem Basisraum \(B=\M\), da die Punkte \(p \in \M\), welche die Vektorräume erzeugen, aus diesem Raum entnommen werden. Ein erster Ansatz für eine globale Struktur ist die Vereinigung

\[\bigcup_{p\in\M} T_p\M.\]

Wir wollen diese Idee im folgenden Beispiel veranschaulichen.

Example 4.5 (Tangentialräume an Einheitskreis)

Sei als zu Grunde liegende Mannigfaltigkeit der Einheitskreis \(\M = \mathbb{S}^1\subset\R^2\) gegeben. Wir wählen als Repräsentanten für jeden Punkt

\[p=(\cos(\alpha), \sin(\alpha))\in\M, \quad \alpha\in (0,2\pi) \setminus \{\pi\}\]

die Kurve

\[\gamma_p(t) := p - t \cdot\big(1, \frac{\cos(\alpha)}{\sin(\alpha)}\big),\]

und somit erhalten wir anschaulich die in Abb. 4.5 für einige Punkte visualisierte Menge.

Es fällt auf, dass sich zwar einzelne Kurven schneiden können, jedoch die Kurven selbst und die assoziierten Vektorräume nicht gleich sind. Um diese Tatsache zu verdeutlichen ist es praktisch die disjunkte Vereinigung

\[\bigsqcup_{p\in\M} T_p\M := \bigcup_{p\in\M} \{p\} \times T_p\M \cong \bigcup_{p\in\M} \{p\} \times \R\]

zu betrachten. Für den Einheitskreis erhalten wir durch die Isomorphie \(T_p\M \cong \R\) so den Zylinder in Abb. 4.6.

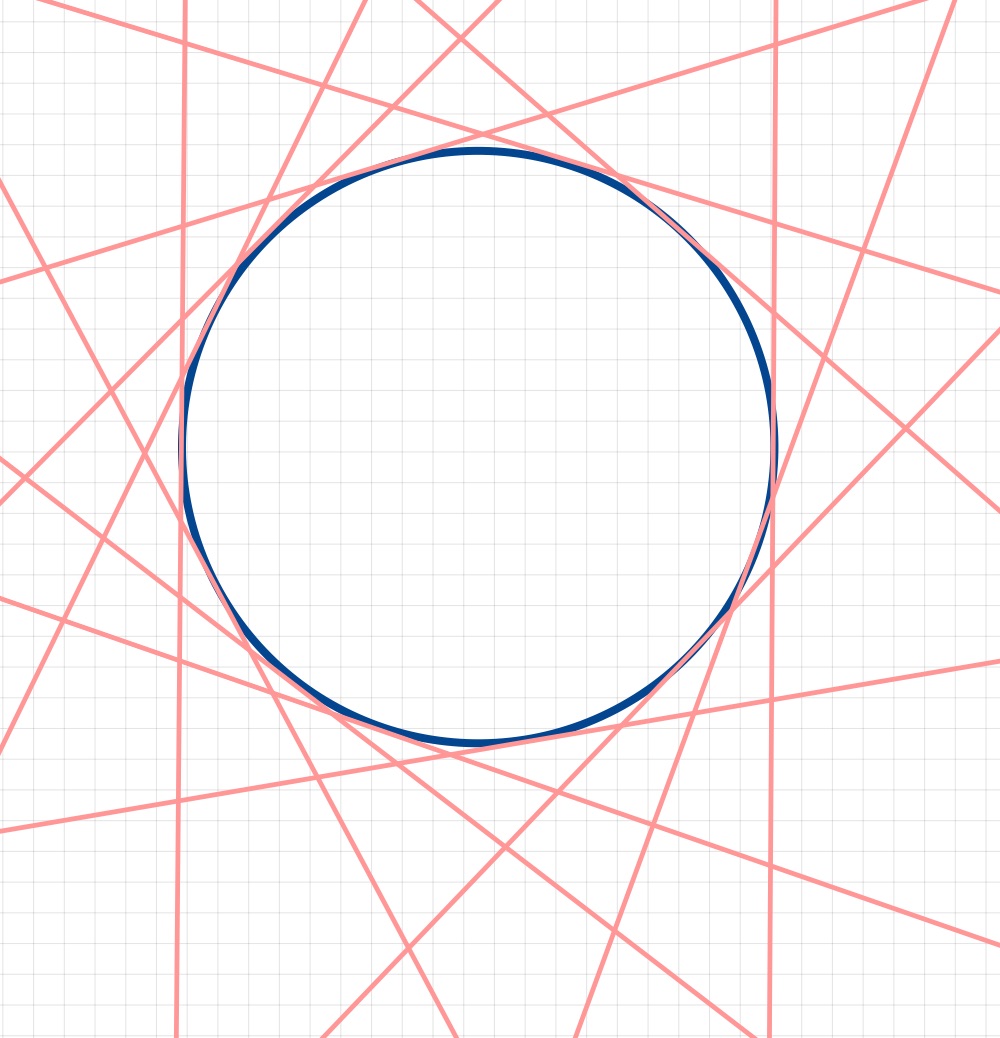
Abb. 4.5 Visualisierung der Tangentialräume einiger Punkte am Einheitskreises.

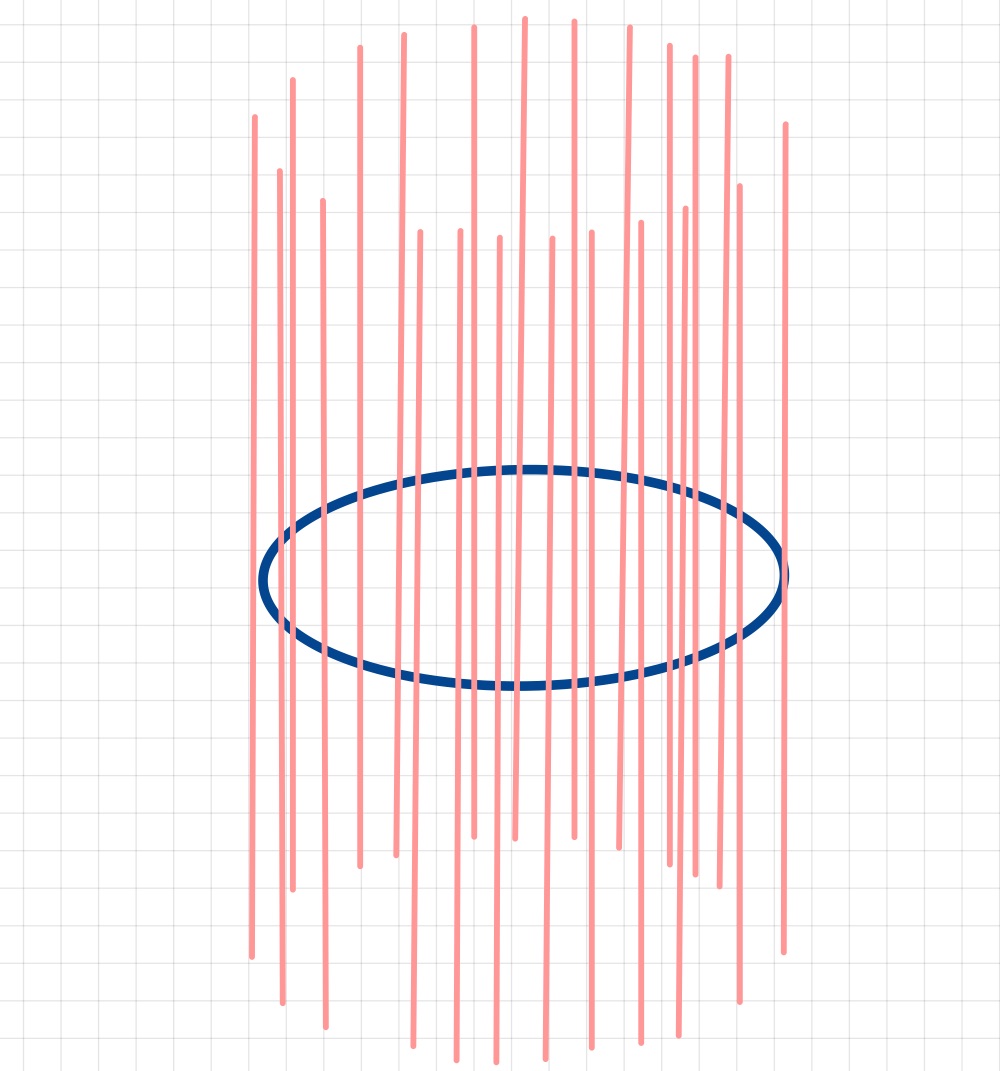
Abb. 4.6 Visualisierung der disjunkt vereinigten Tangentialräume einiger Punkte am Einheitskreises.

Wir wollen diese globale Struktur der disjunkten Vereinigung formal definieren.

Definition 4.19 (Tangentialbündel)

Es sei \(\M\) eine glatte Mannigfaltigkeit. Dann heißt die Menge

\[T\M := \bigsqcup_{p\in\M} T_p\M = \bigcup_{p\in\M} \{p\} \times T_p\M\]

zusammen mit der Projektion

\[\begin{split}\pi:T\M &\to \M\\ \{p\}\times T_p\M &\mapsto p\end{split}\]

das Tangentialbündel von \(\M\).

Insbesondere erkennen wir, dass wir mit Hilfe der Projektion \(\pi\) jedem Element des Tangentialbündels eindeutig den zu Grunde liegenden Punkt \(p\in\M\) zuordnen können, der den entsprechenden Tangentialraum erzeugt hat.

Im Folgenden wollen wir uns zwei Beispiele für Tangentialbündel an Mannigfaltigkeiten ansehen.

Example 4.6 (Tangentialbündel)

1. Sei \(\M=\R^n\). Dann ist das Tangentialbündel gerade gegeben durch

\[T\M = \R^n\times\R^n = \R^{2n}.\]

2. Wie bereits in Example 4.5 gesehen erhalten wir für \(\M=\mathbb{S}^1\) als Tangentialbündel den unendlich hohen Zylinder

\[T\M = \mathbb{S}^1\times \R.\]

In den bisher betrachten Beispielen haben wir als Tangentialbündel jeweils eine Menge der Form \(\M\times \R^n\) erhalten. Dies ist jedoch nicht immer der Fall wie wir sehen werden. Tatsächlich bilden Tangentialbündel von dieser Form eine spezielle Unterklasse.

Definition 4.20 (Triviale Tangentialbündel und parallelisierbare Mannigfaltigkeiten)

Sei \(\M\) eine glatte \(n\)-dimesnionale Mannigfaltigkeit. Das Tangentialbündel \(T\M\) heißt trivial, falls gilt

\[T\M\cong \M\times\R^n.\]

In diesem Fall nennt man die Mannigfaltigkeit \(\M\) auch parallelisierbar.

Remark 4.6

Es lässt sich zeigen, dass \(\mathbb{S}^1, \mathbb{S}^3,\mathbb{S}^7\) die einzigen paralleslisierbaren Sphären sind (siehe [Lee03]). Die Tatsache, dass \(\mathbb{S}^2\) nicht parallelisierbar ist wird beim Satz vom gekämmten Igel in prf:ref{TODO} erneut auftauchen.

Wir wollen uns nun mit der Frage beschäftigen, wie sich die Tangentialräume für unterschiedliche Punkte \(p,q\in B\) des Basisraums zueinander verhalten, insbesondere wenn \(p\) und \(q\) nahe beieinander liegen. Hierbei hilft es das abstrakte Konzept eines Vektorbündels zu betrachten.

Definition 4.21 (Vektorbündel)

Es seien \(\M\) (der sog. Basisraum) und \(E\) (der sog. Totalraum) zwei glatte Mannigfaltigkeiten und \(\pi:E\to \M\) sei glatt und bijektiv. Weiterhin gelte Außerdem sei \(\pi:E\to \M\) eine glatte und bijektive Abbildung. Weiterhin gelte

• für jeden Punkt \(p\in \M\) sei die sogenannte Faser \(E_p:= \pi^{-1}(p)\) ein \(n\)-dimensionaler Vektorraum,

• für jeden Punkt \(p\in \M\) existiere eine offene Umgebung \(U\subset \M\) und ein Diffeomorphimus \(\Psi: \pi^{-1}(U)\to U\times\R^n\), so dass für alle \(x\in U\) gilt

\[\begin{split}\text{pr}_U(\Psi(x)) &= \pi(x)\quad\forall x\in \pi^{-1}(U)\\ \Psi\rvert_{E_q}&: \pi^{-1}(q) \to \{q\}\times \R^n \text{ ist ein Isomorphismus, für alle }q\in U.\end{split}\]

Dann heißt \((E,\M,\pi)\) Vektorbündel vom Rang \(n\). Hierbei bezeichnet \(\text{pr}_U(q, z):= q\) die Projektion auf die \(U\)-Komponente eines Vektors \((q,z)\in U\times\R^n\).

Remark 4.7 (Bündel-Notation)

Anstatt das Vektorbündel \((E,\M,\pi)\) als Tripel aufzuschreiben, ist es üblich von einem Bündel \(E\overset{\pi}{\to}\M\) oder sogar \(E\to\M\) zu sprechen. Die Abbildung \(\pi\) wird im zweiten Fall nur implizit vorausgesetzt.

Die Funktion \(\Psi\) nennt man in diesem Kontext lokale Trivialisierung, denn sie erlaubt es uns den Totalraum \(E\) lokal als Produktraum darzustellen. Analog zum Tangentialbündel nennen wir ein Vektorbündel trivial, falls eine Trivialsierung \(\Psi:E\to \M\times\R^n\) existiert, so dass gilt

\[E \cong \M\times\R^n.\]

Example 4.7

Möbius-Band.

Wir wollen nun zeigen, dass das Tangentialbündel ein Vektorbündel ist. Dazu benötigen wir zunächst die Hilfsaussage des folgenden Lemmas, dass das Tangentialbündel \(T\M\) selbst eine glatte Mannigfaltigkeit ist.

Lemma 4.8

Es sei \(\M\) eine glatte \(n\)-dimensionale Mannigfaltigkeit. Dann ist das Tangentialbündel \(T\M\) eine glatte \(2n\)-dimensionale Mannigfaltigkeit. Insbesondere ist

\[\begin{split}\pi:T\M &\to \M\\ \{p\}\times T_p\M &\mapsto p\end{split}\]

eine glatte und bijektive Abbildung.

Proof. Wir werden lediglich die Idee skizzieren, für den vollständingen Beweis siehe Proposition 3.18 in [Lee03]. Wir benutzen hier die algebraische Definition des Tangentialraums.

Es sei \((U,\varphi)\) eine Karte. Wir betrachten die Menge \(\pi^{-1}(U)\subset T\M\) und die Abbildung

\[\begin{split}\psi:\pi^{-1}(U) \to \phi(U)\times \R^{n}\subset\R^{2n}\\ (p,v) &\mapsto (\varphi(p), v(\varphi)),\end{split}\]

wobei wir für \(v\in T_p\M\subset (C^\infty(\M))^\ast\) die Notation

\[v(\varphi) := (v(\varphi_1),\ldots, v(\varphi_n))\]

benutzt haben. Es stellt sich dann heraus, dass so definierte Abbildungen \(\psi\) Karten auf \(T\M\) und somit tatsächlich auch eine Mannigfaltigkeit definieren. Insbsondere ist ein so definiertes \(\psi\) ein Diffeomorphismus.

Mithilfe der obigen Aussage können wir nun zeigen, dass \(T\M\) ein Vektorbündel ist.

Lemma 4.9

Es sei \(\M\) eine glatte \(n\)-dimensionale Mannigfaltigkeit mit dem Tangentialraum

\[T\M:= \bigsqcup_{p\in\M} T_p\M = \bigcup_{p\in\M} \{p\} \times T_p\M\]

und der Abbildung

\[\begin{split}\pi:T\M\to \M\\ \{p\}\times T_p\M\mapsto p.\end{split}\]

Dann ist \((T\M, \M, \pi)\) ein Vektorbündel vom Rang \(n\).

Proof. Es sei \((U,\varphi)\) eine Karte für \(\M\). Dann definieren wir die Abbildung

\[\begin{split}\Psi: \pi^{-1}(U) &\to U\times \R^n\\ (p,v) &\mapsto (p, v(\varphi)).\end{split}\]

Wir erkennen sofort, dass \(\Psi\) linear ist und dass \((\text{pr}_U\circ\Psi)(p,v) = p = \pi(p,v)\) gilt. Da \(\phi\) ein Diffeomorphismus ist, ist

\[\begin{split}\phi\times\text{Id}:U\times \R^n &\to \phi(U)\times\R^n\\ (p,z) &\mapsto (\phi(p), z)\end{split}\]

ebenfalls ein Diffeomorphismus. Hierbei bemerken wir aber, dass gilt

\[\big((\phi\times\text{Id})\circ \Psi\big)(p,v) = (\phi\times\text{Id})(p, v(\varphi)) = (\phi(p), v(\varphi)).\]

Somit entspricht \((\phi\times\text{Id})\circ \Psi\) gerade der Karte aus dem Beweis von Lemma 4.8 und ist somit auch ein Diffeomorphismus. Daraus folgt aber, dass \(\Psi\) schon ein Diffeomorphismus sein muss.

4.2.3. Vektorfelder

Wir führen zunächst sogenannte Schnitte auf Bündeln ein. Anschaulich abstrahieren wir hierdurch das Konzept von Funktionsgraphen. Es sei \(f:\M\to\R^n\) eine vektorwertige Funktion auf einer Mannigfaltigkeit \(\M\). Dann ist ihr Graph gegeben durch

\[\{(p,f(p)): p\in\M\}\subset \M\times\R^n.\]

Hierbei sehen wir, dass \(\M\times\R^n\overset{\pi}{\to}\M\) ein triviales Bündel ist mit

\[\pi(p,(f(p))) = p.\]

Verallgemeinert betrachten führt diese Überlegung auf folgende Definition.

Definition 4.22 (Glatter Schnitt)

Es sei \(\M\) eine glatte Mannigfaltigkeit und \(E\overset{\pi}{\to}\M\) ein Vektorbündel. Für eine offene Umgebung \(U\subset\M\) heißt eine glatte Abbildung

\[\sigma: U\to E\]

lokaler glatter Schnitt, falls

\[\pi(\sigma(p)) = p\quad\text{ für alle }p\in U.\]

Die Menge der glatten Schnitte auf \(U\) wird mit \(\Gamma(E\rvert_U)\) bezeichnet. Falls die Umgebung \(U\) die ganze Mannigfaltigkeit ist, d.h., es gilt \(U=\M\), dann heißt \(\sigma\) glatter Schnitt und wir definieren \(\Gamma(E):=\Gamma(E\rvert_\M)\).

Für offenen Mengen im Euklidischen Raum kennen wir bereits den Begriff Vektorfeld. Hierbei handelt es sich nämlich um eine Funktion

\[F:U\to\R^n,\]

wobei \(U\subset\R^n\) eine offene Umgebung ist. Wir nehmen in diesem Fall also Punkte \(x\in\R^n\) und ordnen ihnen Vektoren \(F(x)\in\R^n\) aus dem gleichen Raum zu.

Betrachten wir statt offener Mengen \(U\subset\R^n\) nun glatte Mannigfaltigkeiten \(\M\), so stellt sich a priori die Frage in welchen Raum Vektorfelder abbilden sollen. Es stellt sich heraus, dass der Tangentialraum \(T\M\) die richtige Wahl des Zielraums darstellt. Somit können wir das Konzept von Vektorfeldern verallgemeinern indem wir sie als Schnitte des Tangenialraums auffassen.

Definition 4.23 (Glatte Vektorfelder)

Es sei \(\M\) eine glatte Mannigfaltigkeit. Wir nennen einen glatten Schnitt

\[X:\M\to T\M\]

ein glattes Vektorfeld. Das Argument von \(X\) wird hierbei meist als Subskript notiert, d.h., \(X_p := X(p)\).

Für Tangentialbündel haben wir die Abbildung \(\pi:T\M\to\M\) durch

\[\pi(p,v):= p\quad\text{ für } (p,v)\in\{p\}\times T_p\M\]

definiert. Ist \(X\) nun ein glattes Vektorfeld, so gilt

\[\pi(X(p)) = p\]

und somit insbesondere \(X_p\in T_p\M\). Ein Vektorfeld ordnet also jedem Punkt \(p\in\M\) ein Element seines Tangentialraums zu. Falls \(\M\) eine offene Menge in \(\R^n\) ist, ist dies insbesondere konsistent zur bekannten Definition von Vektorfeldern in Euklidischen Räumen.

4.2.3.1. Wirkung von Vektorfeldern

Von der algebraischen Definition des Tangentialraums ist das totale Differential \(df_p\in T^\ast_p\M\) bekannt, welches für \(D\in T^{\text{alg}}_p\M\) und eine Funktion \(f\in C^\infty(M)\) definiert ist durch

\[df_p(D):= D(f).\]

Mithilfe dieses mathematischen Werkzeugs können wir nun die Wirkung eines Vektorfelds definieren.

Definition 4.24 (Wirkung von Vektorfeldern)

Es sei \(\M\) eine glatte Mannigfaltigkeit und \(X\in\Gamma(T\M)\). Die Wirkung von \(X\) auf \(C^\infty\) ist definiert durch

\[\begin{split}X(\cdot):C^\infty(M) &\to C^\infty(\M)\\ f &\mapsto [p\mapsto X_p(f) := df_p(X)].\end{split}\]

4.2.3.2. Lokale Basis von Vektorfeldern

Aus Abschnitt 4.2.1.3 wissen wir bereits, dass wir für jeden Punkt \(p\in\M\) die entsprechenden Tangentialvektoren \(v\in T_p\M\) durch die partiellen Derivationen \(\partial_{x^i}^p\) darstellen können. Im Kontext von Tangentialbündeln stellt sich die natürliche Frage, wie sich diese Vektoren verändern, wenn der Punkt \(p\in\M\) variiert wird. Hierzu definieren wir zunächst folgende Abbildungen.

Definition 4.25 (Lokale Koordinatenfelder)

Es sei \(\M\) eine glatte \(n\)-dimensionale Mannigfaltigkeit und \((U,\phi)\) eine Karte. Dann definieren wir die sogenannten lokalen Koordinatenfelder für \(i=1,\ldots,n\) durch

\[\begin{split}\partial_{x^{i}}&:\M\to T\M\\ \partial_{x^{i}}(p)&:= \partial_{x^{i}}\rvert_p. \end{split}\]

Mithilfe dieser lokalen Koordinatenfelder können wir nun Vektorfelder lokal darstellen.

Lemma 4.10

Es sei \(\M\) eine glatte Mannigfaltigkeit und \((U,\phi)\) sei eine Karte von \(\M\). Dann gilt für \(X\in\Gamma(T\M\rvert_U)\) und die Koeffizientenfunktionen \(X^i:=X(\phi_i)\in C^\infty(U)\), dass gilt

\[X = \sum_{i=1}^n X^i \partial_{x^{i}}.\]

Proof. Es sei \(p\in\M\) ein beliebiger Punkt der Mannigfaltigkeit. Dann haben wir wegen Theorem 4.2 die Darstellung

\[X_p = \sum_{i=1}^n X_p(\phi_i) \partial_{x^i}^p.\]

Mit der Definition 4.24 der Wirkung von Vektorfeldern folgt dann schon

\[X = \sum_{i=1}^n X(\phi_i) \partial_{x^i}.\]

Aus der obigen Darstellung folgt auch, dass lokal für eine Karte \((U,\phi)\) die Wirkung auf \(f\in C^\infty(U)\) geschrieben werden kann als

\[X(f) := \sum_{i=1}^n X^i \frac{\partial f}{\partial_{x^i}}.\]

4.2.4. Das Kotangentialbündel

Analog zum Kotangentialraum, können wir auch das Kotangentialbündel definieren.

Definition 4.26

Es sei \(\pi:T\M\to\M\) eine Tangentialbündel, dann ist das Kotangentialbündel \(\pi^\ast: T^\ast\M\to\M\) mit der Menge

\[T^\ast\M := \bigsqcup_{p\in\M} T_p\M\]

und der Projektion

\[(\pi^{\ast})^{-1}(p):= \{p\}\times T_p^\ast\M\]

definiert.

Remark 4.8

Per Definition ist eine Projektion \(\pi^\ast\) surjektiv und besitzt eine Rechtsinverse \(\pi^\ast\), weshalb obige Definition impliziert, dass für alle \(p\in\M\)

\[\pi({p}\times T_p^\ast\M) = \pi((\pi^{\ast})^{-1}(p)) = p\]

gilt. Insbesondere hat aber jedes Element \(x\in T^\ast\M\) eine Darstellung \(x=\{p\}\times T_p^\ast\M\) für ein \(p\in\M\), weshalb man \(\pi\) wie oben angegen tatsächlich über die Inverse definieren kann.

Auch in diesem Fall erhält man ein Vektorbündel.

Lemma 4.11

Es sei \(\pi:T\M\to\M\) eine Tangentialbündel, dann ist das Kotangentialbündel \(\pi^\ast:T^\ast\M\to\M\) ein Vektorbündel.

Proof. Der Beweis funktioniert analog zum Beweis von Lemma 4.9. Für die Details zur Argumentation weshalb auch \(T^\ast\M\) eine Mannigfaltigkeit ist, verweisen wir auf [Lee03] Prop. 11.9.

Wir interessieren uns auch hier für glatte Schnitte, welche in diesem Kontext als 1-Differentialformen bezeichnet werden.

Definition 4.27

Ein glatter Schnitt \(\omega\in\Gamma(T^\ast\M)\) wir als 1-Differentialform bezeichnet, zusätzlich benutzen wir die Notation

\[\Omega^1(\M) := \Gamma(T^\ast\M)\]

Man kann hier analog lokale Koordinaten Kovektorfelder definierne indem man lokale Koordinaten betrachtet und die duale Basisdarstellung des Kotangentialraums benutzt.

Definition 4.28 (Lokale Koordinatenfelder)

Es sei \(\M\) eine glatte \(n\)-dimensionale Mannigfaltigkeit und \((U,\phi)\) eine Karte. Dann definieren wir die sogenannten lokalen Koordinaten Kovektorfelder für \(i=1,\ldots,n\) durch

\[\begin{split}dx^{i}:\M&\to T^\ast\M\\ p&\mapsto dx^{i}_p. \end{split}\]

Die definierten 1-Formen sind die einfachsten Beispiele der allgmeinen Diffenerentialformen, welche wir in Abschnitt 4.3.1 untersuchen werden. Das Konzept des Kotangentialbündels und der Differentialform ist nun noch etwas abstrakt, allerdings erhalten wir mithilfe des totalen Differentials Definition 4.18 erneut eine einfache Veranschalichung.

Example 4.8

Es sei \(\M\) eine glatte Mannigfaltigkeit und \(f\in C^\infty(\M)\), dann ist die Abbildung

\[\begin{split}df:\M\to T^\ast\M\\ p\mapsto (p, df_p)\end{split}\]

eine Differentialform, wobei \(df_p\in T_p^\ast\M\) für eine Derivation \(D\in T_p\M\) definiert ist durch

\[df_p(D) := D(f),\]

weil \(D\) als Derivation gerade eine lineare Abbildung \(D:C^\infty\to\R\) ist.

Für die Glattheitseigenschaft verweisen wir auf [Lee03] Prop. 10.22., was zeigt, dass \(df\) eine glatte Abbildung ist. Desweiteren sehen wir, dass

\[\pi^\ast(df(p)) = \pi^\ast((p,df_p)) = p \]

und somit gilt per Definition diese Eigenschaft eines Schnittes. Sei nun \((U,\varphi)\) eine Karte mit lokalen Koordinaten \(\varphi = (x^1,\ldots, x^n)\). Für \(p\in\M\) und \(D\in T_p\M\) Derivation gilt nach ??, dass

\[D = \sum_{i=1}^n D(x^i)\, \partial_{x^i}^p = \sum_{i=1}^n dx^{i}(D)\, \partial_{x^i}^p,\]

wobei hierbei \(dx^{i}:T_p\M\to\R\) eine Element der dualen Basis ist. Daraus folgt für das totale Differential an \(p\), \(df_p:T_p\M\to\R\), per Defintion dass

\[df_p(D) = \sum_{i=1}^n dx_p^{i}(D)\, df_p(\partial_{x^i}^p) = \sum_{i=1}^n dx_p^{i}(D)\, \partial_{x^i}^p(f)\]

gilt. Somit gilt also lokal in \(U\)

\[df = \sum_{i=1}^n dx^{i}\, \partial_{x^i}(f).\]

Für den Fall, dass die Mannigfaltigkeit \(\M\) eine offene Teilmene des \(\R^n\) ist erhalten wir einen einfachen Zusammenhang zur klassischen Richtungsableitung.

Example 4.9

Es sei \(\M=U\subset\R^n\) eine offene Teilmenge, für jedes \(p\in\M\) können wir den Tangentialraum dann mit dem \(\R^n\) identifizieren und erhalten, dass das totale Differential an \(p\) gegeben ist durch

\[\begin{split}df_p:\R^n&\to\R\\ v&\mapsto \langle \nabla f(p), v \rangle = \sum_{i=1}^n \partial_i f(p)\, v^i.\end{split}\]

Insbsondere ist \(dx^{i}\) in diesem Fall die Funktion welche einen Vektor auf seine Komponenten abbildet, somit gilt

\[dx^{i}(v) = v^i\]

und daher insgesamt wiederum

\[df = \sum_{i=1}^n \partial_i f, dx^{i}.\]

Zusätzlich haben wir hier auch eine lokale Basisdarstellung als analoges Resultat zu Lemma 4.10 hier nun aber mit den Basiselementen des Kotangentialraums, bzw. den lokalen Koordinaten Kovektorfeldern.

Lemma 4.12

Es sei \(\M\) eine glatte \(n\)-dimensionale Mannigfaltigkeit und \((U,\phi)\) eine Karte mit lokalen Koordinaten \(\varphi=(x^1,\ldots, x^n)\), dann gilt für jede Differentialform \(\omega\in\Omega^1(U)\), dass

\[\omega = \sum_{i=1}^n f_i dx^i\]

wobei \(f_i\in C^\infty(\M)\) gegeben ist durch \(\omega(\partial_{x^i})\).

Proof. Siehe z.B. [Lee03] Seite 282.

4.2.5. Tensorfelder

Als natürliche Verallgemeinerung wollen wir nun das Konzept der Felder auf Mannigfaltigkeiten von Vektoren auf Tensoren übertragen. Um ein Tensorfeld definieren zu können müssen wir zunächst klären, wie das Tensorprodukt von Tangentialbündeln aussehen soll. Für zwei Vektorbündel \(E\overset{\pi_E}{\to}{\M}, F\overset{\pi_F}{\to}{\M}\) wissen wir, dass für jedes \(p\in\M\) die Fasern \(E_p, F_p\) endlichdimensionale Vektorräume sind. Insbeonsdere können wir also das Tensorprodukt

\[E_p\otimes F_p\]

betrachten und damit ein Bündel auf dem Totalraum

\[E\otimes F:= \bigsqcup_{p\in\M} E_p\otimes F_p\]

betrachten. Die entsprechende Projektion \(\pi_{E\otimes F}:E\otimes F\to\M\) ist gegeben durch

\[\pi_{E\otimes F}^{-1}(p):= E_p\otimes F_p := (E\otimes F)_p.\]

Lemma 4.13

Es sei \(E\overset{\pi_E}{\to}{\M}\) ein Vektorbündel vom Rang \(k\) und \(F\overset{\pi_F}{\to}{\M}\) ein Vektorbündel vom Rang \(l\), dann ist

\[\pi_{E\otimes F}:(E\otimes F)\to \M\]

ein Vektorbündel vom Rang \(kl\).

Proof. Siehe Übung.

Die Definition des Tensorbündels lässt sich direkt auf mehrfache Tensorprodukte übertragen und führt uns direkt auf gemischte Tensorbündel.

Definition 4.29

Es sei \(\M\) eine glatte Mannigfaltigkeit, und \(r,s\in\N_0\), s.d. \(r+s>0\), dann heißt

\[T^r_s\M := \bigsqcup_{p\in\M} T^r_s(T_p\M) \to \M\]

Tensorbündel der Stufe \((r,s)\).

Mit den vorherigen Überlegungen können wir direkt schlussfolgern, dass wir hier erneut ein Vektorbündel definiert haben. Insbesondere, da nach Corollary 3.4

\[T^r_s(T_p\M) \cong \underbrace{T_p\M\otimes\ldots T_p\M}_{r\text{ mal}}\otimes\underbrace{T_p^ast\M\otimes\ldots T_p\ast\M}_{s\text{ mal}}\]

gilt erhalten wir die Bündelstruktur über Anwendung von Lemma 4.13.

Corollary 4.1

Es sei \(\M\) eine glatte Mannigfaltigkeit, und \(r,s\in\N_0\), s.d. \(r+s>0\), dann ist \(\pi:T^r_s\M\to\M\) mit der kanonisch nach Lemma 4.13 definierten Abbildung \(\pi\) ein Vektorbündel.

Proof. Folgt direkt aus Lemma 4.13.

Da wir die Struktur eines Vektorbündels definiert haben können wir nun auf natürliche Weise auch Tensorfelder als glatte Schnitte definieren.

Definition 4.30 (Tensorfelder)

Es sei \(\M\) eine glatte Mannigfaltigkeit, und \(r,s\in\N_0\), s.d. \(r+s>0\), ein Tensorfeld ist ein glatter Schnitt \(A\in \Gamma(T^r_s\M)\).

Dank der lokalen Darstellung von Vektorbündeln in Lemma 4.10 können wir die recht abstrakten Tensorfelder lokal sehr konkret Darstellen.

Corollary 4.2

Es sei \(\M\) eine glatte \(n\)-dimensionale Mannigfaltigkeit, \((U,\varphi)\) eine Karte mit lokalen Koordinaten \(\varphi=(x^1,\ldots,x^n)\). Für \(r,s\in\N_0\), s.d. \(r+s>0\) und \(A\in \Gamma(T^r_s\M)\) ein Tensorfeld existieren glatte Koeffizientenfunktionen \(A^{i_1,\ldots, i_s}_{j_1,\ldots,j_r}\in C^\infty(\M)\) für \(i_1,\ldots, i_s, j_1,\ldots, j_r\in \{1,\ldots,n\}\), s.d.,

\[A = A^{i_1,\ldots,i_s}_{j_1,\ldots,j_r} \partial_{x_{i_1}}\otimes\ldots\otimes \partial_{x_{i_r}}\otimes dx^{j_1}\otimes\ldots\otimes dx^{j_s}.\]

Proof. Folgt aus Lemma 4.10 und Lemma 4.12, für Details siehe [Lee03] Prop. 12.19.

Ähnlich zu den Überlegungen in Abschnitt 3.2.6 können wir auch hier das Tensorprodukt von Tensorfeldern betrachten.

Lemma 4.14

Es sei \(\M\) eine glatte Mannigfaltigkeit, für \(r,l\in \N\) seien \(A\in \Gamma(T^r_0\M), B\in \Gamma(T^l_0\M)\) zwei Tensorfelder und \(f\in C^\infty(\M)\), dann sind \(fA\) und \(A\otimes B\) Tensorfelder mit lokalen Koeffezienten

\[\begin{split}(fA)_{i_1,\ldots i_{k}} = f A_{i_1,\ldots, i_k}\\ (A\otimes B)_{i_1,\ldots,i_{l+r}} = A_{i_1,\ldots, i_l} B_{i_{l+1},\ldots, i_{l+k}}.\end{split}\]

Proof. Siehe [Lee03] Prop. 12.22.

zurück

4.1. Differenzierbare Mannigfaltigkeit

weiter

4.3. Differentialformen auf Mannigfaltigkeiten