7. Gewöhnliche Differentialgleichungen¶
Differentialgleichungen spielen seit je her eine fundamentale Rolle bei der physikalischen Modellierung von Naturgesetzen und erklären viele beobachtbare Phänomene unseres Alltags äußerst präzise. Eine Differentialgleichung beschreibt häufig das Änderungsverhalten von Größen, wie zum Beispiel die Fallgeschwindigkeit eines Steins, den man fallen lässt, oder die Vermehrung von Bakterien in einer Nährlösung. Während insbesondere in der Analysis die Existenz und Eindeutigkeit von Lösungen von Differentialgleichungen untersucht wird, widmet sich die Numerische Mathematik der Herleitung von Lösungsverfahren, die approximative Lösungen für Differentialgleichungen liefern, für die keine analytische Lösung bekannt ist.
Mathematisch gesehen ist eine Differentialgleichung eine Gleichung, in der eine unbekannte Funktion und ihre Ableitungen auftreten. Die größte vorkommende Ableitung bestimmt hierbei die Ordnung der Differentialgleichung. Je nachdem ob die es sich um eine Funktion in einer oder mehreren Veränderlichen handelt sprechen wir von einer Gewöhnlichen Differentialgleichung oder einer Partiellen Differentialgleichung. Werden gleich mehrere solche Funktionen durch mehrere Gleichungen beschrieben, so spricht man von einem Differentialgleichungssystem. Im Folgenden beschränken wir uns auf die Diskussion von gewöhnlichen Differentialgleichungen, d.h., wir untersuchen Gleichungen in denen eine unbekannte Funktion mit einer Variablen und deren Ableitungen vorkommen.
Das folgende Beispiel soll ein grundlegendes Verständnis von gewöhnlichen Differentialgleichungen und den zugehörigen mathematischen Fragestellungen liefern.
Example 7.1
Das einfachste Beispiel einer gewöhnlichen Differentialgleichung ist gegeben durch
Wir suchen also eine unbekannte Funktion \(x \colon \R \rightarrow \R\), deren Ableitung gerade die Funktion selbst ist. In diesem Fall können wir die Lösung der Gleichung quasi erraten, denn für die Exponentialfunktion gilt offensichtlich
Jedoch ist dies nicht die einzige Lösung, denn die konstante Nullfunktion \(x(t) \equiv 0\) für alle \(t\in \R\) erfüllt ebenfalls die Differentialgleichung.
In diesem Kapitel wollen wir uns damit beschäftigen, wann Lösungen einer Differentialgleichungen existieren und in welchen Fällen diese eindeutig sind. Darüber hinaus lernen wir praktische Werkzeuge zur analytischen Lösung von Differentialgleichungen kennen.
Wir beginnen mit der Definition einer grundlegenden Klasse von Differentialgleichungen.
Definition 7.1 (Lineare Differentialgleichung)
Sei \(n\in \N\) und \(I \subset \R\) ein offenes Intervall. Seien außerdem \(a_i \colon I \rightarrow \R\) und \(b \colon I \rightarrow \R\) stetige Funktionen für \(0 \leq i \leq n\). Dann nennen wir eine gewöhnliche Differentialgleichung \(n\)-ter Ordnung mit einer unbekannten \(n\)-mal stetig differenzierbaren Funktion \(x \colon I \rightarrow \R\) linear, wenn sie in folgender Form vorliegt
Hierbei bezeichnen wir mit \(x^{(k)}(t)\) die \(k\)-te Ableitung der Funktion \(x\) im Punkt \(t \in I\).
Ist eine Differentialgleichung nicht in der Form (7.1), so bezeichnen wir sie als nichtlinear.
Eine lineare Differentialgleichung heißt homogen, falls \(b(t) \equiv 0\) für alle \(t\in\R\). Der Term \(b\) wird auch häufig Störfunktion genannt.
Im Folgenden wollen wir verschiedene gewöhnliche Differentialgleichungen diskutieren und gemäß der Definition Definition 7.1 klassifizieren.
Example 7.2 (Radioaktiver Zerfall)
Sei \(c>0\) eine Konstante. Dann beschreibt die folgende gewöhnliche Differentialgleichung
den radioaktiven Zerfall eines strahlenden Materials mit Stoffmenge \(x\) zum Zeitpunkt \(t\). In diesem Kontext beschreibt \(c\) die charakteristische Zerfallskonstante des Materials. Es handelt sich hierbei um eine lineare, gewöhnliche Differentialgleichung erster Ordnung, die homogen ist (da die Störfunktion \(b(t) \equiv 0\) ist).
Ist die anfängliche Stoffmenge \(x_0 \in \R^+\) zum Zeitpunkt \(t=0\) mit \(x(0) = x_0\) bekannt, so ist
die eindeutige Lösung der Differentialgleichung. Wir erhalten im allgemeinen Fall also eine einparametrige Schar von Lösungen, die linear vom Anfangswert \(x_0\) abhängen.
Example 7.3 (Steinwurf)
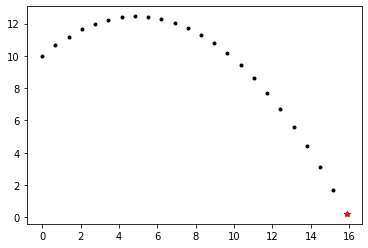
In diesem Beispiel wollen wir die Bahn eines geworfenen Steins im konstanten Gravitationsfeld der Erde mit Erdbeschleunigung \(g \approx 9,81 \frac{m}{s^2}\) berechnen. Wir vernachlässigen die Krafteinflüsse der Luftreibung und betrachten das folgende \textbf{inhomogene System von gewöhnlichen Differentialgleichungen zweiter Ordnung}:
Wir bezeichnen hierbei die Horizontalkomponente der Position des Steins entlang der Wurfbahn zum Zeitpunkt \(t \in \R_0^+\) mit \(x_1 \colon \R_0^+ \rightarrow \R\) und die Vertikalkomponente mit \(x_2 \colon \R_0^+ \rightarrow \R\). Die anfängliche Position zum Zeitpunkt \(t_0 \in \R_0^+\) und die Anfangsgeschwindigkeit seien gegeben als
Unter diesen Voraussetzungen können wir das obige Differentialgleichungssystem lösen und erhalten für die Wurfbahn des Steins, d.h., die Position des Steins in Abhängigkeit der Zeit \(t\in\R_0^+\), folgende Lösung
Hieraus lassen sich nun auch die Richtungskomponenten der Geschwindigkeit des Steins in Abhängigkeit der Zeit \(t\in\R_0^+\) ermitteln, denn es gilt
import matplotlib.pyplot as plt
import numpy as np
import ipywidgets as wdg
import time
def get_plot(z_1 = 0, z_2 = 0, w_1 = 0, w_2 = 0):
t = np.linspace(0,20,30)
g = 9.81
x_1 = z_1 + w_1 * t
x_2 = z_2 + w_2 * t - 1/g * t**2
return x_1, x_2
x_1, x_2 = get_plot(z_2 = 10, w_1 = 1, w_2 = 1)
idx = np.min(np.where(x_2<0))
fig = plt.figure();
plt.plot(x_1[:idx], x_2[:idx], '.', color = 'k');
plt.plot(x_1[idx-1], x_2[idx-1], '*', color='r');
Example 7.4
Beschleunigung eines Raumschiffs durch Gravitation :label: ode:raumschiff
Im letzten Beispiel wollen wir die Wirkung der Gravitation eines Himmelskörpers, wie zum Beispiel der Erde, auf ein wesentlich kleineres Objekt (wie ein Raumschiff) beschreiben. Sei also \(r \colon \R_0^+ \rightarrow \R_0^+\) der Abstand des Raumschiffs zur Erde und \(M \approx 5,972 \cdot 10^{24}~\text{kg}\) die ungefähre Erdmasse.
Dann lässt sich die Beschleunigung, die das Raumschiff auf Grund der Gravitation der Erde erfährt, durch folgende \textbf{gewöhnliche Differentialgleichung zweiter Ordnung}, welche \textbf{homogen und nichtlinear} ist, beschreiben:
Das bedeutet, dass die Beschleunigung des Raumschiffs durch die Gravitation quadratisch mit dem Abstand zum Erdmittelpunkt zunimmt.
