1.2. Wiederholung: Koordinatensysteme und der Satz des Pythagoras¶
Eine elementares Resultat der Euklidischen Geometrie ist der Satz des Pythagoras, der meist als
formuliert wird, wobei \(a\) und \(b\) die Katheten und \(c\) die Hypothenuse eines rechtwinkeligen Dreiecks sind. Wir können den Satz von Pythagoras aber auch völlig anders interpretieren, indem wir ein Koordinatensystem in die Katheten legen, sodass die Eckpunkte \((0,0)\), \((a,0)\), und \((a,b)\) sind. Dann sind die Katheten die Vektoren \((a,0)\) und \((0,b)\) und die Hypothenuse der Vektor \((a,b)\). Der Satz des Pythagoras sagt dann, dass die Länge des Vektors \(v=(a,b)\) gleich \(\sqrt{a^2+b^2}\) ist. Dies bezeichnen wir als die Euklidische Norm eines Vektors (in der Schule auch Betrag eines Vektors)
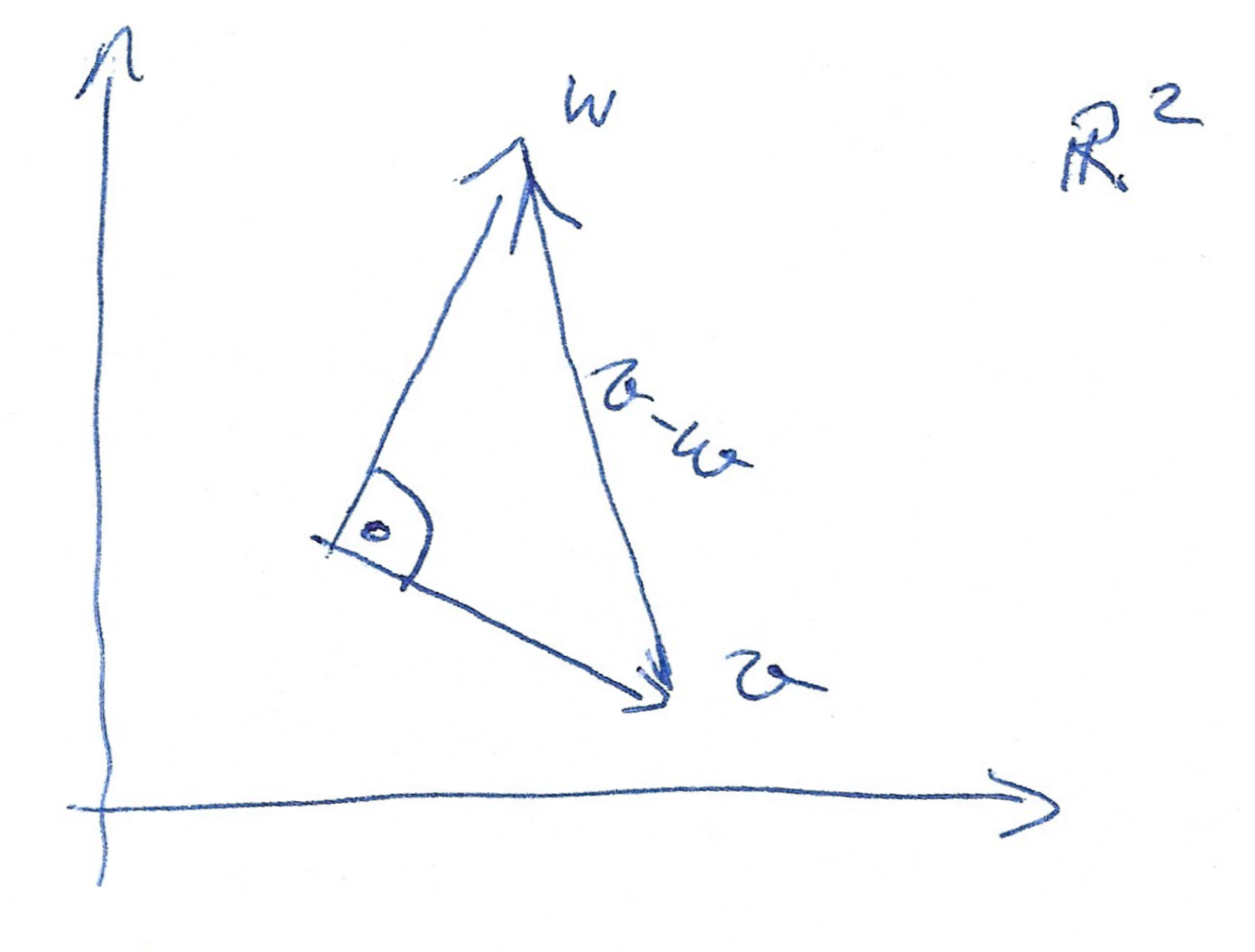
Basiereend auf der Vektordarstellung können wir auch einen einfachen Beweis des Satz des Pythagoras in einer allgemeinen Version geben. Seien \(v=(x_1,x_2)\) und \(w=(y_1,y_2)\) zwei Vektoren im \(\R^2\). Wie üblich definieren wir ihr Skalarprodukt als
Wir beachten, dass \(\Vert v \Vert^2 = v \cdot v\) gilt. Wir nennen zwei Vektoren orthogonal zueinander, wenn \(v \cdot w = 0\) gilt, im \(\R^2\) bedeutet dies einen Winkel von 90 Grad. Nun können wir den Satz des Pythagoras folgenderma{\ss}en formulieren: Sind \(v,w \in \R^2\) zwei zueinander orthogonale Vektoren, dann gilt in der Euklidischen Norm
Wir benutzen die Darstellung über die Euklidische Norm
Wir werden sehen, dass wir solche Strukturen stark verallgemeinern können. Ein analoges Resultat gilt im \(\R^n\) für beliebiges \(n\) mit dem Euklidischen Skalarprodukt
Tatsächlich kann man dies viel weiter verallgemeinern, es genügt einen Raum zu haben, in dem man ein Skalarprodukt definieren kann, das in jeder Komponente linear und symmetrisch ist, sowie \(v \cdot v > 0 \) für \(v \neq 0\) erfüllen. Dann ist durch
immer eine Norm definiert.
Eine wichtige Ungleichung in diesem Zusammenhang ist die Cauchy-Schwarz Ungleichung
bzw. im \(\R^n\)
Für \(n=1\) ist die Cauchy-Schwarz Ungleichung besonders einfach: Sie besagt, dass das Produkt zweier reeller Zahlen kleiner als das Produkt ihrer Beträge ist.
Eine verwandte Ungleichung ist die Young’sche Ungleichung
die aus der Cauchy-Schwarz Ungleichung und der elementaren Ungleichung
für \(a,b \in \R\) folgt. Insgesamt ist die Young’sche Ungleichung aber nur eine Umformulierung von
was wegen der Nichtnegativität der Norm klar ist. Noch einfacher als die Young’sche Ungleichung ist die Dreiecksungleichung
die in einer Dimension (für den Betrag) durch Fallunterscheidung nachgewiesen werden kann. Im Fall der Euklidischen Norm kann man wegen der Nichtnegativität äquivalent beide Seiten quadrieren und die Quadrate der Normen wegkürzen, man endet dann genau bei der Cauchy-Schwarz Ungleichung.
Für den Beweis der Cauchy-Schwarz Ungleichung betrachten wir zunächst die triviale Ungleichung
für \(\lambda \in \R\). Wir können uns auf den Fall \(w \neq 0\) beschränken, da die Cauchy-Schwarz Ungleichung sonst klarerweise erfüllt ist, und wählen \(\lambda = \frac{v\cdot w}{\Vert w \Vert^2}\),
und nach Umstellen folgt die Ungleichung.
